5. ZKIP
ZKIP
1. 개념 및 정의
영지식 증명(ZKIP, Zero-Knowledge Interactive Proof)은 이름 그대로 “지식(정보)을 전혀 노출하지 않으면서(Zero-Knowledge), 상대방에게 내가 그 지식을 알고 있다는 사실만을 상호작용(Interactive)을 통해 증명(Proof)하는 방법”이다.
1) Idea
- 상황: 증명자(Prover)는 “나는 비밀을 알고 있어”라고 주장하고, 검증자(Verifier)는 그 말이 사실인지 확인하고 싶어 한다.
- 목표: Prover는 비밀 자체는 절대 건네주지 않으면서(X 표시), Verifier에게 자신이 비밀을 알고 있다는 사실만 확신시켜야 한다.
2) Properties
영지식 증명이 성립하려면 다음 세 가지 조건이 반드시 만족되어야 한다.
- 완전성 (Completeness)
- 만약 Verifier가 진짜로 비밀을 알고 있다면, Prover는 (절차를 따랐을 때) 이를 반드시 받아들여야 한다.
- 완전성 (Completeness)
- 건전성 (Soundness)
- 만약 Verifier가 증명을 받아들일 수 있다면, Prover는 진짜로 비밀을 알고 있는 것이다.
- 건전성 (Soundness)
- 영지식성 (Zero-knowledgeness)
- 검증 과정이 끝난 후, Verifier는 Prover가 비밀을 알고 있다는 사실 외에는 비밀에 대한 어떠한 추가 정보도 얻을 수 없어야 한다.
- 영지식성 (Zero-knowledgeness)
3) Example
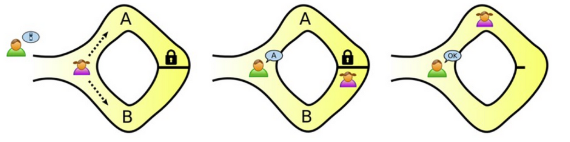
알리바바와 40인의 도둑에서, 어떻게 문을 여는지 보여주지 않으면서, 내가 문을 여는 방법을 안다는 것만 증명할 수 있을지 생각해 보자.
- Verifier는 동굴 밖에서 기다리고, Prover는 A와 B 중 하나를 택하여 동굴로 들어간다.
- Verifier는 참가자에게 A와 B 중 하나의 길로 나올 것을 요구한다.
- Verifier가 요구한 길로 Prover가 나온다.
- 반복
2. 이론적 증명 방법
1) IP(Interactive Proof)의 정의
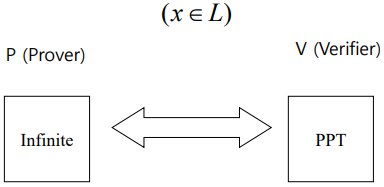
대화형 증명 시스템(Interactive Proof System, IP)은 증명을 두 당사자 간의 ‘대화 과정’으로 정의하는 모델이다.
여기서 두 당사자와 명제는 다음과 같이 정의할 수 있다.
- Prover: 무한한 계산 능력을 가진 존재
Verifier: 현실적인 계산 능력을 가진 존재
- $L$: 참인 모든 정보들 (e.g. 안쪽에 문이 있는 동굴들의 집합)
- $x$: $x \in L$임을 증명하려고 하는 대상 (e.g. 동굴)
- $w$: $x \in L$임을 입증해주는 비밀 정보 (e.g. 주문)
Language L이 IP에 속한다는 것은 다음과 같은 Completeness와 Soundness를 만족한다는 것을 증명하면 된다.
Completeness
$x \in L$ 일 때, Verifier가 Prover(비밀을 알고 있음)를 $\frac{2}{3}$이상의 확률로 Accept 한다.
($\text{if} \quad x \in L, Prob(V(x)=1) \geq \frac{2}{3}$)※ Prover와 Verifier가 Honest
즉, 알리바바의 예시에서 동굴이 통과 불가능한 동굴이라면, 주문을 알고 있는 도둑은 알리바바가 나오라는 곳으로 나올 확률이 높다.
Soundness Error
$x \notin L$ 일 때, Verifier는 Prover(비밀을 모름)를 $\frac{1}{3}$이하의 확률로 Accept 한다.
($\text{if} \quad x \notin L, for \forall P^*, Prob(V(x)=1) < \frac{2}{1}$)※ Prover는 Dishonest, Verifier는 Honest
즉, 알리바바의 예시에서 동굴이 통과 불가능한 동굴이라면, 도둑은 알리바바를 속일 확률이 낮다.
증명의 종류
- Proof of Membership: 어떤 값($x$)가 참인 집합($L$)에 속한다는 사실 자체만 증명하는 것
- Proof of Knowledge: 어떤 값($x$)이 참인 집합($L$)에 속한다는 사실을 증명할 증거($w$)를 알고 있음을 증명하는 것
(이때, Prover에게 $w$가 주어지기 때문에 Prover의 Computing Power를 현실적인 계산능력으로 제한한다.)
2) ZKIP의 정의
※ Prover는 honest, Verifier는 Dishonest
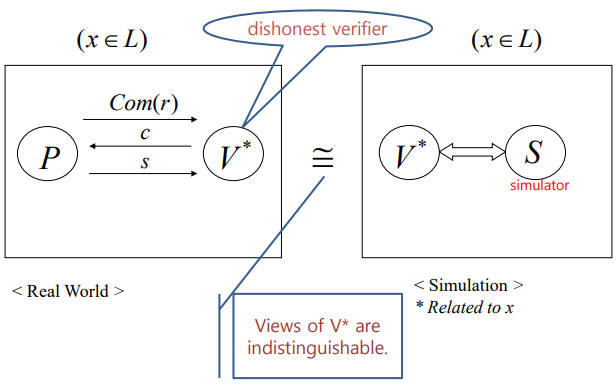
ZK를 만족하는 IP라는 상황은 Real Word와 Simulation이라는 개념으로 증명할 수 있다.
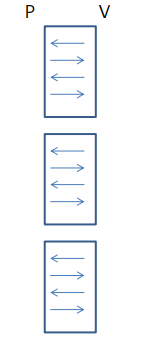
- Real World: 비밀을 가진 대상과의 IP를 기록한 것
- Simulation: 조작된 Real World 영상(Dishonest한 Verifier가 제한된 정보를 가지고 임의로 만들어 봄)
만약, Real World의 확률 분포와, Simulation의 확률 분포가 비슷하다면, Verifier는 이로부터 유의미한 정보를 얻을 수 없다는 것이 된다.
즉, Zero-Knowledge를 만족한다.
Simulation의 목표는 Real World 영상과 100% 동일한 영상을 만드는 것이고, 여기서 어떠한 편집도 허용된다.
즉, 조작을 통해 마치 증명자가 비밀을 알고있는 것처럼 만드는 것이 목표이다.예를 들어, 알리바바의 예시는 Simulation으로 다음과 같이 만들 수 있다.
- Prover가 비밀을 모를 때: 실패 상황을 모두 편집하여 100% 성공하는 영상을 만든다.
- Prover가 비밀을 알 때: 실패 상황이 없다.
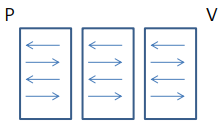
마찬가지로 Real World 시나리오는 다음과 같다.
- Prover는 비밀을 알고 있으므로 항상 100% 성공한다.
즉, 이 상황에서는 남들이 보았을 때, 어떤 것이 Real World이고 어떤 것이 Simulation인지 판별할 수 없다.
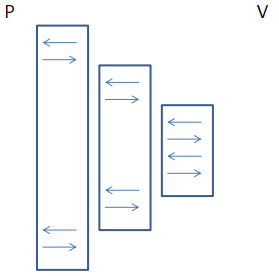
하지만, 알리바바의 예시에서 Prover는 항상 입구의 반대편으로 나와야 한다는 지시를 받았다고 하자.
이 경우 Simulation은 무슨일이 있어도 Prover가 성공하는 영상을 만들 수 없다.
즉, 이 상황에서는 Real World 시나리오와 Simulation을 판별할 수 있기 때문에 ZK라고 정의할 수 없다.
(두 상황에서의 확률 분포가 달라짐)Level of Zero-Knowledge
계산적 영지식 (Computational ZK): 계산 능력이 제한된 컴퓨터로는 두 기록을 구별할 수 없음. (가장 일반적)
통계적 영지식 (Statistical ZK): 두 확률 분포의 차이가 무시할 수 있을 정도로 작음. 무한한 계산 능력이 있어도 구별하기 매우 어려움.
완전 영지식 (Perfect ZK): 두 기록의 확률 분포가 수학적으로 완벽하게 동일함
3. 확장 개념
1) NIZK
Non-Interactive Zero-Knowledge로 비 대화형 ZK 방식이다. 주로 블록체인에서 많이 사용한다.
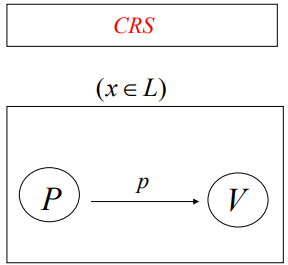
기존의 영지식 증명은 증명자와 검증자가 여러 번의 메시지를 주고받아야 했다(Interactive). 하지만 NIZK는 증명자가 단 한 번의 메시지를 보내는 것만으로 증명을 끝내는 방식이다.
- 필수 조건
- CRS(Common Reference String), 증명자와 검증자가 공유하는 무작위 문자열이 필요하다
2) Composition(합성)
Sequential Composition Parallel Composition Concurrent Composition 증명을 한 번 끝내고,
그다음 증명을 시작여러 개의 증명을 동시에 시작 여러 증명이 비동기적으로
서로 다른 속도로 동시에 진행안전하지만 오래걸림 영지식성이 깨질 위험 존재 영지식성이 깨질 위험 존재
4. 주요 프로토콜
QRP(Quadratic Residuosity Problem)
ZKIP 프로토콜은 수학적으로 풀기 어려운 문제 중 대부분 QRP에 기반을 두고 있다.
어떤 수 $v$에 대해 $\gcd(v, n)=1$이고 $n=pq$일 때, $v \equiv x^2 \pmod n$을 만족하는 $x$가 존재하면 $v$를 n에 대한 Quadratic Residue라고 표현한다. (n에서 제곱근이 존재)
여기서 x는 Secret이 되고, v는 공개키가 된다. 즉, v의 제곱근(x)를 알고 있다는 것을 증명하는 것이 목표가 된다.
예를 들어, $n=15$라고 하면 15랑 서로소인 $z^* = [1, 2, 4, 7, 8, 11, 13, 14]$를 구할 수 있다. 이 중 $\bmod 15$에서 제곱근을 갖는 수는 다음과 같다.
- $v = 1$
- $\equiv 1^2 \equiv 4^2 \equiv 11^2 \equiv 14^2 \pmod 15$
- $v = 1$
- $v = 4$
- $\equiv 2^2 \equiv 7^2 \equiv 8^2 \equiv 13^2$
- $v = 4$
즉, 1과 4는 15에 대한 Quadratic Residue라고 한다. (단순히 n과 v를 알고 있다고 x를 찾는 것은 매우 어려운 문제이다.)
※ Quadratic Residue는 항상 4개의 x를 찾을 수 있음
1) Fiat-Shamir Protocol
- L: s를 선택하고, $v \equiv s^2 \pmod n$인 $v$를 공개
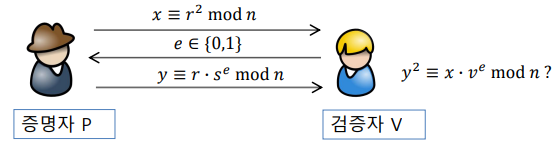
Prover는 임의의 수 $r$을 골라 $x \equiv r^2 \pmod n$을 계산해 보냄
Verifier는 0 또는 1 중 하나의 값($e \in {0, 1}$)을 질문으로 던짐
Prover는 $e=0$이면, $r$을 보내고, $e=1$이면, $r \cdot s$를 보냄
Verifier는 받은 값으로 $y^2 \equiv x \cdot v^3 \bmod n$이 맞는지 확인
Completeness
Prover가 비밀(s)를 알고 있다면 Verifier는 이를 항상 통과시킨다.
Verifier가 확인하는 수식은 $y^2 \equiv x \cdot v^e \pmod n$이다.
Verifier가 $e=0$을 보냈을 때 Verifier가 $e=1$을 보냈을 때 …
Prover: $y = r$을 보냄
Verifier: $r^2 \equiv x$ (성립)…
Prover: $y = rs$를 보냄
Verifier: $r^2s^2 \equiv x v$
$\;\;\equiv r^2 s^2 \pmod n$(성립)※ $x \equiv r^2, v \equiv s^2$
Soundness
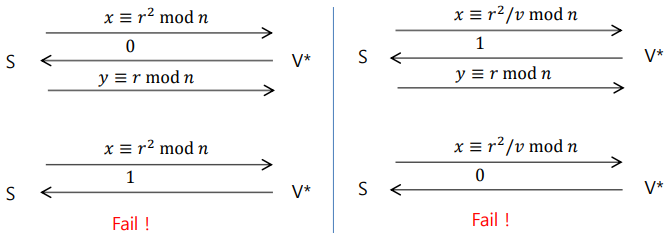
Prover가 사기꾼이라면 질문 e가 0일지 1일지 미리 추측해서 x값을 조작해야 한다.
$e=0$으로 추측 $e=1$로 추측 Prover: $x = r^2$을 설정하여 보냄
Verifer: $e=0$
Prover: $y=r$을 보내고 통과Prover: $x = \frac{r^2}{v}$를 보냄
Verifier: $e = 1$
Prover: $y = r$을 보내고 통과즉, e를 추측하지 못하면 결국 50%의 확률로 정답을 맞출 수 밖에 없다.
Zero-Knowledge
위와 같이 Simulator를 만들고, fail부분을 편집하여 전부 성공하는 장면으로 만들 수 있기 때문에 Real World와 Simulator를 구분할 수 없다.
즉, Zero-Knowledge가 보장된다.
2) Feige-Fiat-Shamir Protocol
- L: $n=pq$를 계산하고 $\gcd(s_i, n)=1$이고 $1 \leq s_i \leq n-1$인 비밀키 벡터 $s = [s_1, s_2, …, s_k]$선택, $v = [v_1, v_2, …, v_k], n$을 공개키로 사용
Prover는 $1 \leq r \leq n-1$인 r을 골라 $x \equiv r^2 \bmod n$을 계산해 보냄
Verifier는 0 또는 1 중 하나의 값을 원소로 갖는 벡터($e_i \in {0, 1}$)를 질문으로 던짐
Prover는 $y \equiv r (s_1^{e_1} s_2^{e_2} … s_k^{e_k} \pmod n)$을 계산해 보냄
Verifier는 $y^2 v_1^{e_1} v_2^{e_2} … v_k^{e_k} \equiv x \pmod n$이 맞는지 확인
※ Fiat Shamir 인증 기법을 순차적으로 k번 수행한 것을 단 한번으로 인증할 수 있음
3) Schnorr Protocol
소인수분해(QRP) 기반이 아닌, 이산 대수 문제(Discrete Logarithm Problem)에 기반한 방식
초기 설정: $v \equiv a^{-s} \pmod p$를 만족하는 비밀값 $s$를 사용
차이점
- 검증자의 질문($e$) 범위가 0, 1이 아니라 매우 큰 범위($1 \le e < 2^t$)
- 질문의 범위가 넓기 때문에 반복 수행 없이 단 한 번의 라운드만으로도 충분히 낮은 확률의 건전성을 확보할 수 있음
vv