5-1. Unconstrained Optimization(Line search)

J. Nocedal and S. J. Wright. Numerical Optimization. Springer, New York, 2nd edition, 2006.

Unconstrained Optimization

문제 정의

\[\min_x f(x), \\ x \in \mathbb{R}^n, n \leq 1, f: \mathbb{R}^n \rightarrow \mathbb{R}\]

• 목표: 컴퓨터의 제한된 Resource를 활용해 주어진 식의 최적해를 찾는 알고리즘을 개발하는 것
• 문제점
  ⅰ) f의 전체적인 형태는 알 수 없다.
  ⅱ) f의 국소적인 정보는 알 수 있지만 이를 최소한으로 활용해야 한다.
  ⅲ) f에 noise가 있을 수 있기 때문에 최적점에 대한 정의가 필요하다.
  

※ 예를 들어 $f(x) =(Y - \phi(\mathbf{t};\mathbf{x}))^2$ ($Y$는 관측값, $\phi(\mathbf{t})$는 예측값, $\mathbf{x}$는 모델의 파라미터)라고 하자. 이때, 우리가 원하는 것은 $f(x)=0$인 모델($\phi(\mathbf{t};\mathbf{x})$)지만 noise나 파라미터의 부족 등 다양한 이유로 실제로는 $f(x)=0$을 만족하지 못한다.

즉, 우리는 들어가기에 앞서 모델이 어떤 파라미터를 가져야 최적의 모델이 되는지에 대한 정의를 내릴 필요가 있다.

1. 최적점의 정의

1) Global minima

\[f(x^*) \leq f(x)\]

즉, 이 함수에서 가장 작은 점을 말한다. 하지만 우리는 f의 local한 정보만을 알 수 있고, 많은 점들을 방문할수록 연산량이 늘어나기 때문에 이를 구하는 것은 매우 어렵다.

2) local minima

\[f(x^*) \leq f(x), \qquad x \in \mathcal{N}\]

즉, 주변의 점(양 옆)에 대해 제일 작은 점을 말한다. 대부분의 알고리즘은 이 local minimizer를 찾는 방식으로 동작한다. 이 local minimizer에는 다음과 같이 여러 종류가 있다.

• weak local minimizer
• strict/strong local minimizer
• isoloated local minimizer

최적화를 하기 위한 함수 $f$에 local minimizer가 많을 경우 global minimizer를 찾는 것은 매우 어렵다. 알고리즘이 local minimizer에 갇힐 확률이 높기 때문이다.

반면에 만약 $f$에 대한 global한 정보(Convex여부)를 알 수 있다면 global minima를 찾기 위한 단서로 활용할 수 있다. Convex function의 가장 중요한 점은 모든 local minimizer가 global minimizer가 된다는 점이기 때문이다.

---

2. 최적점 판별법

$f$가 연속이고 두번 미분가능하다면 다음과 같은 성질을 사용해서 local minima를 판별하는 것이 가능하다.

1) Taylor’s theorem

$f$가 연속이고 미분 가능하면 다음이 성립한다.

\[f(x + p) = f(x) + \nabla f(x + tp)^Tp, \qquad t \in (0, 1)\]

※ 위 정리는 평균값 정리에 의해 유도될 수 있다.
$g(t) = f(x + tp)$라고 할 때, 평균값 정리에 의해 $g(1) - g(0) = g’(t)(1-0), \quad t \in (0, 1)$을 만족하는 값이 반드시 존재한다.

---

이때, $f$가 두번 미분 가능하다고 가정하면 다음 수식이 만족된다.

\[\nabla f(x+p) = \nabla f(x) + \int^1_0 \nabla^2f(x + tp)p dt, \qquad t \in (0, 1)\]

※ 마찬가지로 $\psi(t) = \nabla f(x + tp)$로 정의하자. 이때, 기본 정리에 의해 $\psi(1) = \psi(0) + \int^1_0 \psi’(t) dt$이므로 이를 정리하면 위의 수식을 얻을 수 있다.

---

질문: 이 식은 어떻게 유도된건지 모르겠다…

\[f(x + p) = f(x) + \nabla f(x)^Tp + \frac{1}{2} p^T \nabla^2 f(x+tp)p, \qquad t \in (0, 1)\]

2) First-order Necessary conditions

\[x^* \text{ is local minima}, f \text{ is 미분가능/연속} \rightarrow \nabla f(x^*) = 0\]

---

귀류법을 통해 위 식을 증명할 수 있다.
즉, 만약 \(x^*\)가 local minima라고 할 때, \(\nabla f(x^*) \neq 0\)이라고 하자.
이때, \(p = - \nabla f(x^*)\)라고 정의하면, \(p^T \nabla f(x^*) < 0\)이다. 또한 $\nabla f$가 \(x^*\)근처에서 연속임을 가정했으므로 \(p^T \nabla f(x^* + tp) < 0\)이 성립하는 $t \in [0, T]$가 존재한다.

여기에 Taylor’s theorem을 활용하면 다음과 같은 식을 얻을 수 있다.

\[f(x^* + \bar{t}p) = f(x^*) + \bar{t} p^T \nabla f(x^* + tp)< f(x^*), \qquad t \in (0, \bar{t})\]

즉, \(f(x^*)\)보다 더 작은점이 \(x^*\)주위에 존재하기 때문에 local minima라는 가정에 모순된다.

3) Second-order Necessary conditions

\[x^* \text{ is local minima}, \nabla^2 f \text{ is 존재/연속} \rightarrow \nabla^2 f(x^*) \succeq 0 \; , \nabla f(x^*) = 0\]

---

마찬가지로 귀류법을 통해 위 식을 증명할 수 있다.
만약, \(\nabla^2 f(x^*)\)가 PSD가 아니라면, 우리는 \(p^T \nabla^2 f(x^*) p < 0\)인 점을 선택할 수 있다. 이때, $\nabla^2 f$가 \(x^*\)근처에서 연속임을 가정했으므로 \(p^T \nabla f(x^* + tp) p< 0\)이 성립하는 $t \in [0, T]$가 존재한다.

또한 First-order condition을 적용하면 $\nabla f(x^*)$를 활용할 수 있다.

여기에 Taylor’s theorem을 활용하면 다음과 같은 식을 얻을 수 있다.

\[f(x^* + \bar{t}p) = f(x^*) + \bar{t} p^T \nabla f(x^*) + \frac{1}{2}\bar{t}^2 p^T \nabla^2 f(x^* + tp)p < f(x^*), \qquad t \in (0, \bar{t})\]

즉, \(f(x^*)\)보다 더 작은점이 \(x^*\)주위에 존재하기 때문에 local minima라는 가정에 모순된다.

4) Second-order Sufficient conditions

\[\nabla^2 f \text{ is 존재/연속}, \nabla f(x^*) = 0, \nabla^2 f(x^*) \succ 0 \rightarrow x^* \text{ is strict local minima}\]

---

$\nabla^2 f$가 \(x^*\)에서 연속임이고 PD이기 때문에, 우리는 $r > 0$에서 $\nabla^2 f(x)$가 PD로 정의되는 정의역(ball) $\mathcal{D} = \begin{Bmatrix}z \vert \Vert z-x^* \Vert < r\end{Bmatrix}$을 찾을 수 있다.

이제 여기서 $\Vert p \Vert < r$이 성립하는 nonzero vector p가 있을 때, $p^T \nabla f(z) p > 0$이므로 다음이 성립한다.

\[f(x^* + p) = f(x^*) + p^T \nabla f(x^*) + \frac{1}{2} p^T \nabla^2 f(z) p = f(x^*) + \frac{1}{2}p^T \nabla^2 f(z) p > f(x^*)\]

즉, \(f(x^*)\)보다 더 작은점이 주위에 존재하지 않기 때문에 \(x^*\)에서는 local minimum값을 갖는다.

5) Convex function

\[f \text{ is convex}, \nabla f(x^*) = 0 \rightarrow x^* \text{ is global minima} \\\]

※ 전역 수렴이란? global minimum으로 수렴을 한다는 것이 아닌, 초기값에서 시작했을 때 결국 stationary point에 도달한다는 것을 의미

---

@ 알고리즘

위에서 최적점을 정의하고 어떤 점이 최적점인지 알아보았다. 그러면 이제 이 최적점을 어떻게하면 찾을 수 있을지 알고리즘을 알아보자.

들어가기에 앞서 이 점을 찾는 알고리즘은 크게 두가지로 분류된다. 이때 이 두가지 알고리즘은 모두 다음과 같은 특징을 가지고 있다.

• 시작점에 대한 정의가 필요하다. 이것은 사용자나 알고리즘을 통해 결정한다.
• 시작점에서 시작해 Iterative한 과정으로 최적점을 찾아 나간다.
• $x_k$에서 $x_{k+1}$로 이동하는 알고리즘이다. 이때, $f(x_k) > f(x_{k+1})$가 반드시 성립할 필요는 없지만, 정해진 구간안에 감소해야한다.

위의 공통점을 가지면서 이동 방식(이동 방향, 이동 거리)을 구하는 방법에 따라 다음과 같이 알고리즘을 나눌 수 있다.

Line Search	Trust region
ⅰ. 먼저 방향($p_k$)을 찾아 고정한다. ⅱ. Step size($\alpha_k$)를 찾는다. ⅲ. $\alpha_k$가 조건을 만족하는지 판별한다. ⅳ. 불만족시 $\alpha_k$를 다시 찾는다.	ⅰ. Maximum stepsize $\Lambda_k$를 설정한다. $\quad =$ trust region ⅱ. 이 조건 하에서 $f$를 근사시킬 함수 $m$을 찾는다, ⅲ. $m$에서 방향과 Step size를 찾는다. ⅳ. 조건을 불만족할 시 $\Lambda_k$를 줄인다.

즉, Line search는 방향을 먼저 선택하여 고정한 상태에서 $f$를 감소시키는 이동 거리를 찾는 방식이다. 하지만 trust region 방식은 maximum 이동 거리를 찾고 이 안에서 방향과 이동 거리를 모두 찾는다는 차이점이 있다. 이 차이점을 명심하며 각 알고리즘에 대해 더 자세히 알아보자.

(질문: Chapter 2, page 20, 1번째 문단과 figure 2.4의 해석방법)

※ Scaling

좋은 알고리즘이란 Scale Invariance를 갖는 알고리즘이다. 최적화 문제에서 poorly scaled된 문제를 흔히 접할 수 있는데, 이때는 하나의 변수가 전체 함수 $f$에는 큰 영향을 주는 반면 다른 방향으로는 미미한 영향을 준다.
(ex. $f(x) = 10^9 x_1^2 + x_2^2$)

보통 이를 해결하기 위해서는 Diagonal scaling을 사용하여 새로운 변수($z$)를 사용하여 optimization을 수행한다.

\[\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 10^{-10} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 10^{5}\end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \end{bmatrix}\]

이때, gradient를 이용하는 알고리즘은 이러한 scaling 측면에서 효율적이지 않다는 단점이 있고, Hessian을 사용하는 알고리즘은 scaling 측면에서 매우 효과적인 성능을 보인다.

3. Line search 알고리즘

\[\min_{\alpha > 0} f(x_k + \alpha_k p_k)\]

• 정의
  Line search알고리즘은 위와 같이 특정 방향($p_k$)으로 특정 거리($\alpha_k$)만큼 움직였을 때, 어떻게 하면 가장 작아질 수 있는지를 찾는 알고리즘이다.

• 방향을 정하는 방식들
  
  • Steepest descent
  • Newton’s method
  • Quasi-newton’s method
• Step size를 정하는 방식들
  
  • Backtracking line search

Global convergence를 위해서는 방향과 step size를 모두 잘 선택해야한다.

Zoutendijk 정리

(이 부분은 뒤의 내용을 먼저 이해하고 읽어야 한다.)

line search기반 최적화 알고리즘이 global convergence를 보장한다는 것을 증명하는 정리이다.

• 전제 조건
  ⅰ) 각 iteration에서 $p_k$는 감소방향이고, step size $\alpha_k$는 wolfe조건을 만족한다.
  ⅱ) 함수 $f$는 $\mathbb{R}^n$에서 bound되어 있고, 미분 가능하고 도함수가 연속이다.
  ⅱ) $\nabla f$가 Lipschitz 연속하다. ($\rightarrow \Vert \nabla f(x) - \nabla f(\tilde{x}) \Vert \leq L \Vert x - \tilde{x} \Vert$)

• 결론
  위 조건 하에서 $\sum_{k\geq 0} cos^2 \theta_k \Vert \nabla f_k \Vert^2 < \infty$ 이다.

즉, 이 정리를 통해 $\underset{k \rightarrow \infty}{\lim} \Vert \nabla f_k \Vert = 0$이 성립한다는 것을 알 수 있다.

---

먼저 Wolfe condition(Curvature)과 Lipschitz 연속성 조건을 결합하면 다음과 같은 수식을 얻을 수 있다.

\[(c_2 - 1)\nabla f_k^T p_k \leq (\nabla f_{k+1} - \nabla f_k)^T p_k \leq \alpha_k L \Vert p_k \Vert^2 \\ \alpha_k \geq \frac{c_2 - 1}{L} \frac{\nabla f_k^Tp_k}{\Vert p_k \Vert^2}\]

이를 Wolfe condition(armijo, $f_{k+1} \leq f_k - c_1\alpha_k(-\nabla f_k^T p_k)$)와 결합하면 다음과 같은 식을 얻는다.

\[f_{k+1} \leq f_k - c \frac{(\nabla f_k^T p_k)^2}{\Vert p_k \Vert^2} = f_k - c \cdot cos^2\theta_k \Vert \nabla f_k \Vert^2\]

이 식을 합산하여 다시 정리하면 $f_{k+1} \leq f_0 - c \sum_{j=0}^k cos^2 \theta_j \Vert \nabla f_j \Vert^2$이고, f가 특정 값에 bound되어 있다는 조건을 결합하면 $\sum_{k\geq 0} cos^2 \theta_k \Vert \nabla f_k \Vert^2 < \infty$ 이 성립한다.

이때, search direction $p_k$를 $f$를 감소시키는 방향이라고 정의했으므로 $cos \theta_k \geq \delta > 0$이다. 따라서 위의 식이 성립하기 위해서는 $\underset{k \rightarrow \infty}{\lim} \Vert \nabla f_k \Vert = 0$이어야 한다.

–방향 설정 방식–

간단하게 요약하면 Line search의 경우 매 iteration마다 방향($p_k$)과 Step size($\alpha_k$)를 구해야 한다. 그리고 이를 조합해($x_{k+1} = x_k + \alpha_k p_k$) 다음 좌표를 계산한다. 여기서 방향을 정할 때, 유의할 점은 $p_k$는 $p_k^T \nabla f_k < 0$을 만족하는 값이어야 $f$를 감소시킬 수 있다는 점이다.

이를 증명하기 위해서 Taylor’s theorem(2-1)은 다음과 같이 다시 표현할 수 있다.

\[f(x + \alpha p) = f(x) + \alpha \nabla f(x)^Tp + \frac{1}{2} \alpha^2 p^T \nabla^2 f(x+tp)p\]

이때, 현재 점에서 가장 가파른 방향을 찾아야 하므로 $\alpha_k$가 매우 작다고 하면 2차항은 0으로 근사되므로 다음이 성립한다.

\[f(x + p) \approx f(x) + \alpha \nabla f(x)^Tp\]

즉, 우리는 $p_k^T \nabla f_k < 0$을 만족하는 값을 찾아야 $f$를 감소시킬 수 있다.

이제 이 방향에 대해 구체적으로 알아볼 예정이고, 뒤의 내용을 요약하자면 대부분의 알고리즘에서 이 $p_k$는 다음과 같은 형태를 갖는다.

\[p_k = - B_k^{-1} \nabla f_k \\ B_k \text{ is symmetric and nonsingular matrix}\]

• Steepest descent
  

  $B_k = I$

• Newton’s method
  

  $B_k = \nabla^2 f(x_k)$

• Quasi-Newton’s method
  

  $B_k = B_{k-1} + U$

※ conjugate gradient를 제외한 모든 방식은 trust-region에서도 비슷한 형태로 사용된다.

1) Steepest descent

현재 점($k$)에서 가장 가파르게 감소하는 방향인 $p_k = - \nabla f_k$로 이동 방향을 설정하는 방식이다.

• 장점
  

  미분값만 계산하면 되기 때문에 계산 속도가 빠르다.

• 단점
  

  수렴 속도가 느리다.

※ 이 방향이 왜 가파른 방향이고 감소하는 방향일까?

앞서 살펴보았듯이 \(f(x + p) \approx f(x) + \alpha \nabla f(x)^Tp\)이므로, Line search의 목적함수는 다음과 같이 변경할 수 있다.

\[\min_p p^T \nabla f_k \qquad , \text{subject to } \Vert p \Vert = 1\]

이때, $p^T\nabla f_k = \Vert p \Vert \Vert \nabla f_k \Vert cos \theta = \Vert \nabla f_k \Vert cos \theta$ 이므로 이 값이 가장 작을 때는 $\theta = \pi$일 때이고, $p = - \frac{f_k}{\Vert \nabla f_k \Vert}$임을 알 수 있다.

즉, $p = - \frac{f_k}{\Vert \nabla f_k \Vert}$ 방향에서 f가 가장 가파른 방향이고 $p_k^T \nabla f_k < 0$이므로 감소하는 방향이다.

※ 참고로 $p_k$와 $-\nabla f_k$의 각도가 $\frac{\pi}{2}$미만이라면, f가 감소하는 방향(전역 수렴 방향)이라는 것은 보장된다.

---

Convergence rate

\[f(x) = \frac{1}{2} x^T Q x - b^T x \\ Q \succ 0\]

위 식에서 $Q$가 대칭임을 가정하면 이 고유벡터들이 서로 직교하고, 최적해 $x^*$에서 $f(x)$는 $f(x) = \frac{1}{2}(x - x^*)^T Q (x - x^*) + \text{상수} = \frac{1}{2}(x - x^*)^T V \Lambda V (x - x^*) + \text{상수}$와 같이 쓸 수 있다. 즉, $f$의 등고선은 $Q$의 고유벡터 방향에 따라 정렬된 타원체라는 것을 알 수 있다. 이는 $f$의 이차 형식을 Q의 고유벡터 기준으로 보았을 때, 등고선이 각각의 고유벡터 방향으로 늘어난 타원 형태를 이룬다는 것을 의미한다.

이제 위 사례에서 steepest descent의 step을 살펴보면, $\nabla f(\alpha) = 0$이 되는 값으로 step을 결정한다.

\[\alpha_k = \frac{\nabla f_k^T \nabla f_k}{\nabla f_k^T Q \nabla f_k} \\ x_{k+1} = x_k - (\frac{\nabla f_k^T \nabla f_k}{\nabla f_k^T Q \nabla f_k}) \nabla f_k\]

여기서 $\Vert x \Vert_Q^2 = x^T Q x$라고 정의하고 $Qx^* = b$라는 사실을 이용하면 $\frac{1}{2} = \Vert x - x^* \Vert^2_Q = f(x) - f(x^*)$가 성립함을 유도할 수 있다.

즉, Q norm을 통해 현재 값과 optimal value의 차이를 측정할 수 있게 된다.

이를 사용하면 다시 의 수식을 얻을 수 있다.

\[\Vert x_{k+1} - x^* \Vert_Q^2 = (1 - \frac{(\nabla f_k^T \nabla f_k)^2}{(\nabla f_k^T Q \nabla f_k)(\nabla f_k^T Q^{-1} \nabla f_k)}) \Vert x_k - x^* \Vert^2_Q\]

이때, 괄호 안은 매우 복잡한 수식으로 이루어져있기 때문에, 이를 간단하게 표현하기 위해 다시 조건수의 관점에서 bound하여 표현해보자. Rayleigh quotient의 성질을 이용하면 위 식을 다시 다음과 같이 표현할 수 있다.

\[\Vert x_{k+1} - x^* \Vert_Q^2 = (\frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1})^2 \Vert x_k - x^* \Vert^2_Q \\ 0 < \lambda_1 \leq \lambda_2 \leq ... \lambda_n\]

즉, 이 부등식을 통해 iteration이 반복될 때마다 오차가 일정 비율($\rho = (\frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1})^2 < 1$)로 감소하는 것을 알 수 있다.

• 조건수
  

  Condition number $k(Q) = \frac{\lambda_{\max}}{\lambda_{\min}}$이 작을수록, 즉 모든 고유값이 거의 같으면 $\rho \approx 0$이므로 수렴속도가 매우 빨라진다는 것을 알 수 있다.

  • ※ 이는 Q의 모든 고유값이 같으면, 등고선이 원형이 되기 때문에 steepest descent방향이 항상 최적점 $x^*$를 직접 향하게 되어 수렴속도가 빨라진다는 것을 의미한다. 반면에 등고선이 길쭉하면 지그재그 현상으로 인해 수렴속도가 저하된다.

※ 질문: 그렇다면 일반적인 딥러닝에서도 이 조건수를 활용한 regularization term을 만들어서 활용할 수 있지 않을까?? (SINDER참고)

2) Newton’s method

Taylor근사를 사용해 이동 방향을 $p_k = - (\nabla^2 f_k)^{-1}\nabla f_k$로 설정하는 방식이다.

• 장점
  

  해 근처에서 수렴 속도가 제곱으로 빨라진다.(특히, 해 근처에서 매우 빨라짐)

• 단점
  

  Hessian을 계산해야하기 때문에 많은 비용이 발생한다.

※ Taylor 근사의 minima가 감소하는 방향인 이유?
Line search의 목적 함수는 Taylor 근사를 통해 다음과 같이 표현할 수 있다.

\[f(x_k+p_k) \approx f_k + p^T \nabla f_k + \frac{1}{2} p^T \nabla^2 f_k p \overset{\text{def}}{=} m_k(p)\]

여기서 $\nabla^2 f_k \succ 0 $를 가정하면¹ $f(x_k + p_k) \approx m_k(p)$은 convex function이므로 global minimum은 단순히 $\nabla m_k(p) = \nabla f_k + \nabla^2 f_k p = 0$인 점을 찾음으로써 구할 수 있다. 이때, Positive Definite를 가정했으므로, $\nabla f_k$의 고유값이 모두 양수이고, 따라서 역함수가 존재한다.

즉, $p_k = - (\nabla^2 f_k)^{-1}\nabla f_k$ 이다.

이 정보를 활용하면 $\nabla f_k^T p_k = -p_k^T \nabla^2 f_k p_k \leq -\sigma_k \Vert p_k \Vert^2 \leq 0$이 성립한다는 것을 알 수 있고, 이 방향도 $f$를 감소시킬 수 있다는 것이 보장된다.

※ 1: $\nabla^2 f_k \succ 0$이 아닐 경우 Newton’s method는 성립되지 않는다. 이 때는 $(\nabla^2 f_k)^{-1}$이 존재하지 않을 수 있고(즉, 행렬식 = 0), 만약 존재한다 해도 $\nabla f_k^T p_k^N < 0$ 이 성립한다는 보장이 없기 때문이다. 이러한 상황을 해결하기 위해 실제 알고리즘들은 몇가지 수정 작업을 거친다. (후술 예정)

※ Steepest decent와 다르게 Newton’s method에서는 step size를 보통 1로 설정한다. 이때, 결과가 만족스럽지 않을 경우에 step size를 줄이는 방식으로 구현한다.

---

Convergence rate

$f(x_k)$의 Hessian이 PD가 아닐 경우 Newton의 update방향이 반드시 감소하는 방향이 아닐 수 있다. 하지만, 여기서는 local convergence properties, 즉 해 $x^*$ 근처에서의 동작을 다룰 예정이다. 이 근처에서 Hessain은 PD이고, Newton’s method는 quadratically하게 수렴함을 증명할 수 있다.

• 가정
  ⅰ) $f(x)$가 2번 연속 미분 가능
  ⅱ) $\nabla^2 f(x)$가 Lipschitz 연속($ \Vert \nabla^2 f(x) - \nabla^2 f(\tilde{x}) \Vert \leq L \Vert x - \tilde{x} \Vert$)
  ⅲ) $x^*$에서 Hessian $\nabla^2 f(x^*)$가 Positive Definite
  ⅳ) $x_0$가 $x^*$에 충분히 가까움

Newton’s method($p_k^N = \nabla^2 f_k^{-1} \nabla f_k$)를 사용하므로 다음 수식이 성립한다.

\[x_k + p_k^N - x^* = x_k - x^* - \nabla^2 f_k^{-1} \nabla f_k = \nabla^2 f_k^{-1} [\nabla^2 f_k (x_k - x^*) - (\nabla f_k - \nabla f_*)]\]

또한 Taylor’s theorem에 따르면 $\nabla f_k - \nabla f_* = \int^1_0 \nabla^2 f(x_k + t(x^* - x_k))(x_k - x^*) dt$이 성립한다. 여기에 ⅰ) 삼각 부등식, ⅱ) Lipschitz 연속 조건을 순서대로 적용하면 다음과 같다.

\[\Vert \nabla^2 f(x_k) (x_k - x^*) - (\nabla f_k - \nabla f(x^*)) \Vert \\ = \int^1_0 [\nabla^2 f(x_k) - \nabla^2 f(x_k + t(x^* - x_k))] (x_k - x^*) dt \\ \leq \int^1_0 \Vert \nabla^2 f(x_k) - \nabla^2 f(x_k + t(x^* - x_k)) \Vert \Vert x_k - x^* \Vert dt \qquad \text{(삼각부등식)} \\ \leq \Vert x_k - x^* \Vert^2 \int^1_0 Lt dt = \frac{1}{2} L \Vert x_k - x^* \Vert ^2 \qquad \qquad \qquad \text{(Lipschitz 연속)}\]

이때, $\nabla^2 f(x^*)$가 PD이므로, $x_k \rightarrow x^*$에 따라 $\nabla^2 f(x_k) \rightarrow \nabla^2 f(x^*)$이고, 따라서 $\nabla^2f(x_k)^{-1} \rightarrow \nabla^2 f(x^*)^{-1}$이다. 특히 “충분히 가까운” 거리 r을 적절히 선택하면, $\Vert x_k - x^* \leq r$에서 $\Vert \nabla^2 f_k^{-1} \Vert \leq 2 \Vert \nabla^2 f(x^*)^{-1} \Vert$가 성립한다.

이를 처음에 가정한 식에 대입하면 현재 점($x_{k}$)에 대해 다음 점($x_{k+1}$)이 최적점에 Quadratically하게 수렴함을 알 수 있다.

\[\Vert x_k + p_k^N - x^* \Vert = \Vert x_{k+1} - x^* \Vert \\ \leq L \Vert \nabla^2 f(x^*)^{-1} \Vert \Vert x_k - x^* \Vert^2 \\ = \tilde{L} \Vert x_k - x^* \Vert^2\]

3) Newton’s method with Hessian modification

위에서 보았듯이 Newton’s method는 Hessian matrix($\nabla^2 f(x)$)가 positive definite여야 한다는 특징이 있었다. 하지만 우리는 이 점을 보장할 수 없기 때문에 몇가지 수정 작업을 거쳐서 구현한다.

\[\nabla^2 f(x_k) p_k = - \nabla f(x_k)\]

먼저 newton방법에서는 위의 식에 따라 방향 $p_k$를 구한다. 하지만 만약 Hessian matrix($\nabla^2 f(x)$)가 positive definite가 아니라면(즉, indefinite라면) 이 방향이 descent direction이라는 보장을 할 수 없다.

이 문제를 해결하기 위해 Hessian과 계산 도중에 형성되는 Positive diagonal matrix나 fulll matrix를 더해서 새로운 계수 행렬을 얻어서 활용한다.

즉 $B_k = \nabla^2 f(x_k) + E_k$를 인수분해하고, 만약 $\nabla^2 f(x_k) \succ 0$이면 $E_k = 0$ 그렇지 않으면 $B_k \succ 0$으로 만드는 $E_k$를 적절히 선택한다. 그리고 이 $B_k$를 Hessian대신에 사용하는 방식이다. 이때, 이 $B_k$가 다음 조건을 만족하는 선에서 modified hessian은 전역적 수렴이 보장된다.

• bounded modified factorization property
  

  $k(B_k) = \Vert B_k \Vert \Vert B_k^{-1} \Vert \leq C, \qquad \text{some } C > 0$

Eigenvalue modification

$\nabla^2 f(x_k)$는 Symmetric 행렬이므로, Spectral decomposition이론에 의해 $\nabla^2 f(x_k) = Q\Lambda Q^T = \sum^n_{i=1} \lambda_k q_i q_i^T$로 분해할 수 있다. 여기서 eigenvalue가 음수인 부분($\lambda_iq_iq_i^T$)을 머신 정밀도($\mathbb{u}$)보다 큰 값중 작은 양수($\delta = \sqrt{\mathbb{u}}$)으로 교체하는 것을 Eigenvalue modification이라한다.

\[B_k = A + \Delta A = Q (\Lambda + diag(\tau_i))Q^T, \qquad \tau_i = \begin{cases}0 & , \lambda_i \geq \delta \\ \delta-\lambda_i & , \lambda_i < \delta\end{cases}\]

• 단점
  

  음수였던 eigenvalue를 작은 양수값으로 교체하면 해당 eigenvector 방향에서는 곡률이 매우 작아진다. 즉, 수정된 Hessian에서 계산된 step 방향은 이 방향에 대해 매우 긴 step을 생성할 수 있다.(미분값과 평행하기 때문) 따라서 newton’s method의 장점이었던 quadratic approximation이 유효하지 않을 수 있다.

• example
  

  $\nabla^2 f(x_k) = diag(10, 3, -1), \mathbb{u} = 10^{-16}$이라고 할 때, $B_k = diag(10, 3, 10^{-8})$이다.

• 참고
  

  위 방법 말고도 음수인 eigenvalue를 양수로 뒤집는 방식을 사용할수도 있다.

---

Diagonal modification

Eigenvalue modification같은 경우는 단순히 음수였던 부분만 양수로 만들어주지만, 이 방식은 $\nabla^2 f_k$의 모든 eigenvalue에 같은 값을 더해주어 minimum값이 $\delta$에 근사하도록 만드는 방식을 의미한다. 수식적으로는 다음과 같이 표현할 수 있다. \(B_k = A + \Delta A = A + \tau I, \qquad \tau = \max(0, \delta - \lambda_{\min}(A))\)

※ 이를 Software로 구현할 때는 보통 Hessian에 대해 Spectral decomposition을 직접 사용하지는 않고, 가우시안 소거법을 사용해 수정값을 선택한다.

• 단점
  

  매번 Eigen value를 구하는 것은 매우 비효율적이다. 실제 문제에서는 Hessian이 매우 큰 행렬이 될 수 있고, 또 보통 이를 구현할 때 계산 과정에서 반올림 오차같은 수치적 불안정성이 발생할 수 있다.
  $\rightarrow$ 이를 해결하기 위해 오직 Symmetric에 PSD의 경우에만 Cholesky 분해((표준버전)$A= L L^T$, (변형버전)$A = LDL^T$)가 가능하다는 점을 이용해서 다음과 같은 알고리즘을 만들수 있다.

• Cholesky with Added Multiple of the identity
  

  Diagonal modification에서 decomposition을 사용하는 대신에 Cholesky 분해를 시도해보는 방식이다. 즉, 특정 값 $\tau_0$에서 부터 시작하여 분해가 가능할 때 까지 $2^k \tau_0$를 반복해서 수행하면 $A + \tau I \succ 0$을 만족하는 값을 찾을 수 있다.

• Modified cholesky factorization LDL form
  

  Cholesky분해는 $A = MM^T$방식뿐만 아니라, $A = LDL^T$로도 사용된다. 이 때는 D의 대각 원소들을 개별적으로 검사하고 조정할 수 있기 때문에, 위의 방식보다 더 안정적으로 조정할 수 있다는 장점이 있다.

• Modified symmetric indefinite factorization
  

  4번 알고리즘에 존재하는 문제점(LDL분해 과정에서의 오류 증폭 가능성)을 해결하기 위한 방식으로 다음 성질을 이용
  \(PAP^T = LBL^T \rightarrow P(A + E)P^T = L(B + F)L^T\)

위에서 보았다 싶이 Newton’s method는 매력적인 방법이지만 계산비용이 크다는 단점이 있었다. 이에 이를 해결하기 위한 여러가지 방법이 제안 되었고 이 중 Quasi-newton’s method 방법을 알아보자.

4) Quasi-Newton’s method

Quasi-newton 방식은 Hessian $\nabla^2 f_k$을 직접 구하지 않고 $B_k$라는 근사 행렬을 사용한다. 이때 $B_k$는 각 step마다 업데이트 된다.

\[B_k p_k = -\nabla f_k\]

이 방식에 대한 핵심 idea는 1차 도함수에 대한 변화를 통해 2차 도함수(Hessian)에 대한 정보를 추정할 수 있을 것이라는 점에서 시작된다.

먼저 Taylor’s theorem에서 다음과 같은 수식을 유도할 수 있다.

\[\nabla f(x+p) = \nabla f(x) + \int^1_0 \nabla^2f(x + tp)p dt \\ = \nabla f(x) + \int^1_0 [\nabla^2f(x + tp) - \nabla^2 f(x) ]pdt + \int ^1_0 \nabla^2 f(x) p dt \\ = \nabla f(x) + \nabla^2 f(x) p + \int^1_0 [\nabla^2f(x + tp) - \nabla^2 f(x)]pdt\]

이때, $x_{k+1} = x_k + p$라고 하면, $\nabla f(x_{k+1}) = \nabla f(x_k) + \nabla^2 f(x_k) (x_{k+1}-x_k) + o(\Vert x_{k+1} - x_k \Vert)$이고, 결국 1차도함수의 변화량($\nabla f_{k+1} - \nabla f_k$)은 $\nabla^2 f(x_k) (x_{k+1}-x_k)$과 근사된다는 것을 알 수 있다.

\[\nabla^2 f_k(x_{k+1} - x_k) \approx \nabla f_{k+1} - \nabla f_k\]

즉, 현재 $B_k$가 있다고 하면, 이 값은 이것을 $B_{k+1} s_k = y_k$를 활용해 업데이트할 수 있게 된다. 이때, 보통의 Hessian이 symmetry하다는 점에서 착안해 보통 $B_k$는 symmetry한 행렬로 설정한다.

또 위 형태는 secant equation으로 표현할 수 있다는 것을 알 수 있다.
우리는 $B_{k+1} = B_{k} + U$ 방식으로 업데이트 하면서, 이와 동시에 업데이트 이후에도 “symmetric”이라는 점과 secant equation($(B_k + U)s_k = y_k$)을 만족하도록 하고싶다.
이를 위해서 다음과 같은 모델링 방식을 사용할 수 있다.

• 방법1) symmetric-rank-one(SR1) formula
  

  $B_{k+1} = B_k + \frac{(y_k - B_ks_k)(y_k - B_ks_k)^T}{(y_k - B_ks_k)^Ts_k}$
  (※ 증명: 질문, 이 부분은 아직 잘 이해가 안된다.)

• 방법2) BFGS formula(rank-2 matrix)
  

  $B_{k+1} = B_k - \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k} + \frac{y_ky_k^T}{y_k^Ts_k}$
  (※ BFGS의 초기값 $B_0$이 Positive Definite이고 $s_k^Ty_k > 0$일 경우 $B_k$는 Positive Definite임이 증명 가능하다.)

※ 실제 구현할 때, 몇몇 방식은 B를 업데이트하는게 아니라 $B^{-1}$을 업데이트하는 방식을 사용해 더 간단하게 식을 구성하는 경우도 있다.

※ Newton’s method와 마찬가지로 해 근처에서 매우 빠른 수렴 속도를 갖는다.

기타

• Nonlinear conjugate gradient method
  

  $p_k = -\nabla f(x_k) + \beta_k p_{k-1}$,
  ($\beta_k$는 $p_k$와 $p_{k-1}$이 scalar를 유지하게 만드는 conjugate)

---

–Step size 설정 방식–

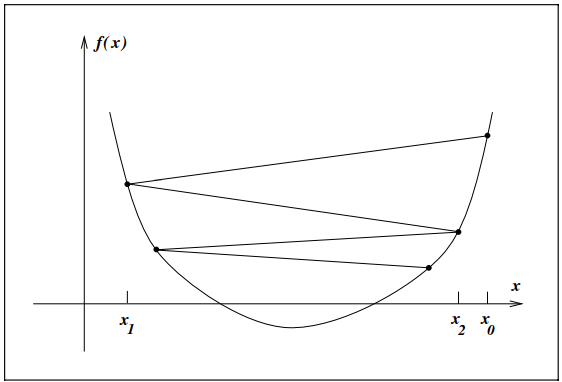
위에서는 $\alpha$가 단순히 $f$를 감소시키는 값이라고 정의하였다. 하지만 이 정의만으로는 아래의 경우와 같이 $f$가 최적의 값에 수렴할 수 있다고 보장할수는 없다.

그렇다고 $\min_{\alpha > 0} f(x_k + \alpha_k p_k)$의 최적화 하는 것은 매우 많은 비용이 든다. 즉, 목표를 최적의 값을 찾는 것이 아닌, $f$를 충분히 감소시키는 값으로 설정해야 하고 이에 대한 정의가 필요하다. 이러한 inexact line search에서는 이를 위해 다음과 같은 조건을 정의한다.

• Wolfe conditions
• Goldstein conditions

위의 방식으로 “충분한 감소” 조건에 대한 정의를 내렸으면, 이제 이 조건을 만족하는 Step size를 결정하면 된다. 이때 이 과정은 다음과 같이 두 단계로 나누어진다.

• Bracketing phase
  

  $\alpha$의 후보들을 순서대로 찾고, 이 중 특정 조건을 만족시키는 구간을 찾는다.

• Selection phase
  

  위에서 찾은 구간 내에서 보간법(Bisection/interpolation)을 통해 더 나은 $\alpha$값을 선택한다.

@ Wolfe conditions

Armijo condition

\[f(x_k + \alpha p_k) \leq f(x_k) + c_1 \alpha \nabla f_k^T p_k \\ c_1 \in (0, 1)\]

즉, $\alpha$만큼 갔을 때 실제 함수가 작아진 양이, 기울기를 이용해 예측한 감소량(1차 근사량 감소량($\alpha \nabla f_k^Tp_k$)에 일정 비율($c_1$, 보통 $10^{-4}$)을 곱한 것) 보다 훨씬 많이 작아야 한다는 것이다.

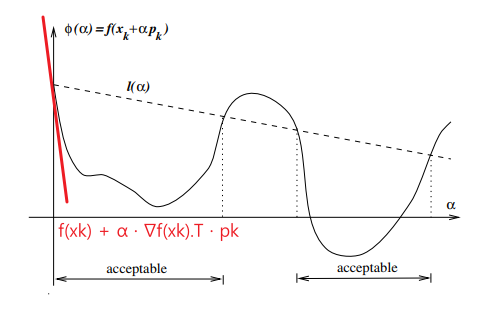
위 식은 이 그림과 같이 표현할 수 있다.

• 빨간색 선 = 현재 점($x_k$)에 접하는 직선
• 점선 = 현재 점($x$)에 접하는 직선에서 기울기를 일정 비율 줄인 직선
• 실선 = $f(x_k + \alpha p_k)$

위에서 $\phi(\alpha) \leq l(\alpha)$가 성립하는 step size($\alpha$)를 구하는게 목표가 된다.

• 한계
  

  이 조건은 $\alpha$가 아주 작은 값이라면 항상 만족시킬 수 있다는 단점이 있다. 이 경우에는 최적화의 진행이 지연될 수 있기 때문이다.

이 한계를 극복하기 위해 다음과 같은 조건이 추가적으로 도입된다.

---

Curvature condition

\[\nabla f(x_k + \alpha_k p_k)^T p_k \geq c_2 \nabla f_k^T p_k\\ c_2 \in (c_1, 1)\]

여기서 좌변은 단순히 $\phi(\alpha)$에 대한 미분값이다. 즉, 다시말해 Step size만큼 이동한 곳에서의 기울기($\phi’(\alpha_k)$)가 현재 기울기($\phi’(0) = \nabla f_k^T p_k$)의 일정 비율($c_2$, 보통 0.9)이상 커야 한다는 조건이다.

이 조건은 움직인 이후의 기울기가 여전히 너무 음수라면(즉 경사가 급하다면) 아직 더 이동할 수 있는 가능성이 있다는 뜻이므로 더 넓은 $\alpha$ 범위에서 찾을 수 있게 만들고, 만약에 충분한 감소가 없다면 line search를 종료할 수 있게 만들어 준다.

---

Wolfe conditions

위의 두 조건(armijo, curvature)을 합친 것이 wolfe conditions라고 한다

이때, Strong wolfe conditions의 개념도 있는데 이는 다음과 같다.

$ vert \nabla f(x_k + \alpha_k p_k)^T p_k \vert \leq c_2 \vert \nabla f_k^T p_k \vert $

보통의 wolfe condition을 만족시키는 점 중 Stationary point(미분값이 0인 점)근처에 있지 않은 점들이 있을 수 있다. 이를 위해서 curvature condition을 수정하여 사용하는데 이를 strong wolfe conditions라고 한다.

---

Lemma

$f: \mathbb{R}^n \rightarrow \mathbb{R}$이 연속하고 미분 가능하고,
$p_k$가 현재 위치($x_k$)에서의 감소방향($p_k$)이고,
$[x_k+\alpha p_k \vert \alpha > 0]$에서 f가 bound이하로 떨어지지 않고,
$0 < c_1 < c_2 < 1$을 가정할 경우 wolfe condition을 만족하는 구간이 반드시 존재한다.

※ 평균값 정리 등을 이용해 증명 가능

@ Goldstein conditions

Goldstein conditions

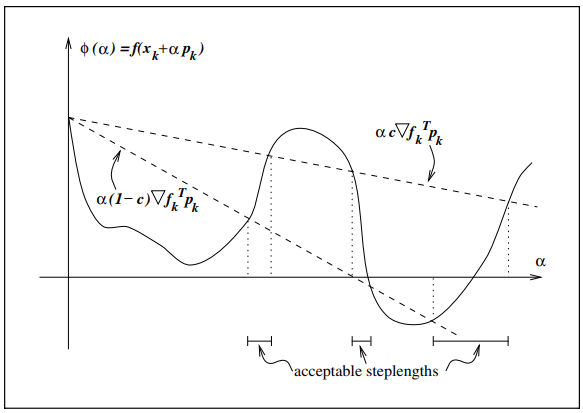
\[f(x_k) + (1-c) \alpha_k \nabla f_k^T p_k \leq f(x_k + \alpha_k p_k) \leq f(x_k) + c\alpha_k \nabla f_k^T p_k \\ 0 < c < \frac{1}{2}\]

두번째 조건(오른쪽)은 위에서 봤던 Armijo condition과 동일하다. 첫번째 조건은 비슷한 방식으로 Step size가 지나치게 작아지지 않도록 조절하는 역할을 한다.

주로 newton-type 알고리즘에 자주 사용되지만 quasi-newton알고리즘에서처럼 Hessian근사를 Positive definite로 유지해야하기 때문에 적합하지 않다.

• 단점
  

  그림에서 볼 수 있듯이 첫번째 조건으로 인해 최적점이 배제될수도 있다.

1) Backtracking Line Search

Wolfstein conditions에서 Curvature condition이 없을 경우 최적화의 진행이 더디게 될 수 있다고 했었다. 하지만 Backtraking 알고리즘을 사용할 경우 이러한 문제는 생략할 수 있다.

def set_params():
    alpha_max = 1
    rho = randon.randrange(0, 1)
    c = randon.randrange(0, 1)
    return alpha_max, rho, c

alpha, rho, c = set_params()
x = now
p = - differential(f, x)

while f(x + alpha * p) <= f(x) - c * alpha * (p**2):
    alpha = rho * alpha

이 그림에서 $\alpha → c, t → \alpha, \beta → \rho$라고 생각하고 보면 된다.

간단하게 보면, 그냥 큰 initial step length $\bar{\alpha}$에서부터 $\rho$를 곱하면서 크기를 줄이다가 armijo condition을 만족하는 순간이 오면 그거부터 쓰자는 것이다. 보통 initial step length($\bar{\alpha}$)는 newton, quasi-newton 에서 1로 사용되지만, steepest descent와 conjugate gradient에서는 다른 값으로 사용된다.

※ 실제로는 $\rho$를 매번 고정하지 않고 “safeguarded interpolation” 등으로 조절하여 더 효율적으로 𝛼를 축소한다.

이 방식은 주로 newton’s method에서 잘 사용되지만 quasi-newton과 conjugate method등에서는 이보다는 Wolfe조건을 더 많이 사용한다.

2) Interpolation

Backtracking line search를 조금 더 개선한 버전으로 가능한 적은 횟수로 $\nabla$를 계산해 효율성을 높이고자 하는 것이 목표이다. Armijo condition은 다음과 같다.

\[\phi(\alpha) = f(x_k + \alpha p_k) \\ \phi(\alpha) \leq \phi(0) + c_1 \alpha_k \phi'(0)\]

이때, $\phi(\alpha)$의 형태를 2차, 혹은 3차함수라고 가정하고, 미리 알고있는 함수를 사용해 이 함수에 대한 계수를 구해 최적의 step size를 찾는 알고리즘이다.

1. 초기값 확인
   

   만약 초기 추정치 $\alpha_0$이 위의 condition을 만족하면 search를 마친다. 그렇지 않으면 아래의 보간법을 사용하 새로운 Step size $\alpha_1$을 구한다.

2. Quadratic Interpolation
   

   $\phi(0), \phi’(0), \phi(\alpha_0)$의 세 정보를 이용해 2차함수 $\phi_q(\alpha)$를 보간하여 다음과 같이 구성한다.
   \(\phi_q(\alpha) = \frac{\phi(\alpha_0) - \phi(0) - \alpha_0 \phi'(0)}{\alpha_0^2}\alpha^2 + \phi'(0)\alpha + \phi(0)\)
   그리고 이 2차함수의 최소점을 구하여 새로운 Step을 구한다. $\alpha_1 = -\frac{\phi’(0)\alpha_0^2}{2[\phi(\alpha_0) - \phi(0) - \phi’(0)\alpha_0]}$

3. Cubic Interpolation
   

   만약 Quadratic Interpolation으로도 적절한 값을 구하지 못하면 $\phi(0), \phi’(0), \phi(\alpha_0), \phi(\alpha_1)$의 네 정보를 이용해 2차함수 $\phi_q(\alpha)$를 보간하여 다음과 같이 구성한다.

\[\phi_c(\alpha) = a\alpha^3 + b\alpha^2 + \alpha \phi'(0) + phi(0) \\ \begin{bmatrix}a \\ b\end{bmatrix} = \frac{1}{\alpha_0^2\alpha_1^2(\alpha_1 - \alpha_0)}\begin{bmatrix}\alpha_0^2 & -\alpha_1^2 \\ -\alpha_0^3 & \alpha_1^3 \end{bmatrix} \begin{bmatrix} \phi(\alpha_1) - \phi(0) - \phi'(0)\alpha_1 \\ \phi(\alpha_0) - \phi(0) - \phi'(0) \alpha_0 \end{bmatrix} \\ \rightarrow \alpha_2 = \frac{-b + \sqrt{b^2 - 3a\phi'(0)}}{3a}\]

※ 만약 3차보간에서도 값을 찾지 못하면 3차 보간을 구할 때 사용했던 $\phi(\alpha_1)$ 대신 이전에 구했던 $\phi(\alpha_2)$를 사용해 다시 Cubic interpolation을 반복한다. 이 과정을 armijo condition을 만족할 때 까지 반복한다.

※ 이 과정에서 $\alpha_i \approx \alpha_{i-1}$이거나, $\alpha$가 너무 작아진다면, $\alpha_i = \frac{\alpha_{i-1}}{2}$으로 재설정한다.

※ 미분값이 쉽게 계산될 수 있는 상황에서는 3차보간에서 이를 활용해 더 그럴듯한 step size를 뽑아내기도 한다.

3) brackets & zoom

※ initial step size

• newton, quasi-newton
  

  $\alpha_0 = 1$
  (1로 잡아야 해 근처에서 빠르게 수렴하는 특성이 발휘된다.)

• steepest descent(1)
  

  $\alpha_0 = \alpha_{k-1} \frac{\nabla f(x_{k-1})^T p_{k-1}}{\nabla f(x_k)^Tp_k}$
  (이전 반복에서의 함수값 변화와 기울기 정보가 현재 반복에서와 비슷할 것이라는 추측을 통해 결정하는 방식이다.
  $\rightarrow \alpha_0 \nabla f_k^T p_k = \alpha_{k-1} \nabla f_{k-1}^T p_{k-1}$)

• steepest descent & newton/quasi-newton
  

  $\alpha_0 = \frac{2 (f_k - f_{k-1})}{\phi’(0)}$
  (질문: 유도 과정이 이해안됨)