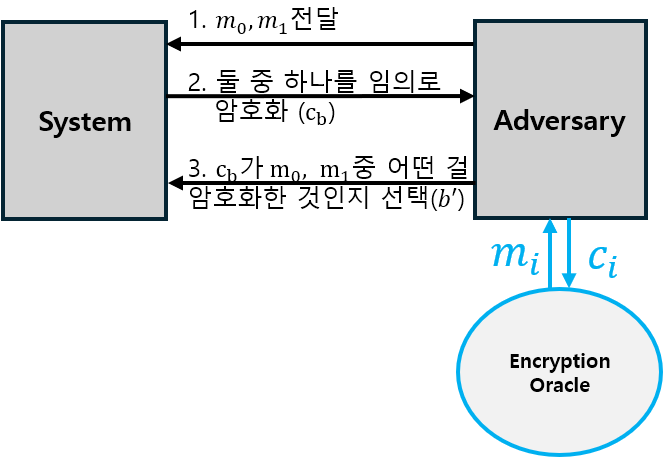
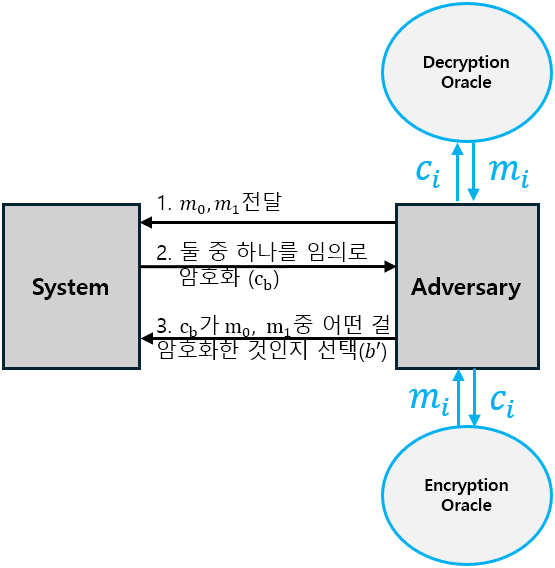
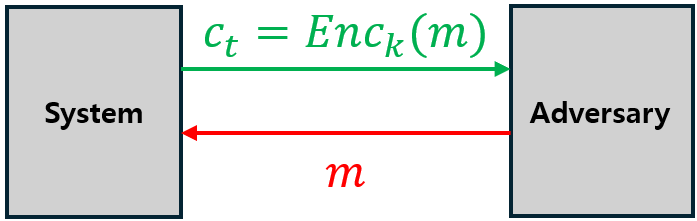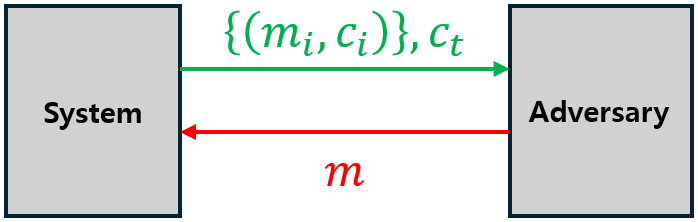2. Security Model
공격 모형
| 종류 | Adversary의 조건 |
|---|---|
| COA (Ciphertext Only Attacks) |  ● Target ciphertext |
| KPA (Known Plaintext Attacks) |  ● Target ciphertext ● Ciphertext of Some Plaintext |
| CPA (Chosen Plaintext Attacks) |  ● Target ciphertext ● Ciphertext of chosen plaintext |
| CCA (Chosen Ciphertext Attacks) |  ● Target ciphertext ● Plaintext of chosen ciphertext |
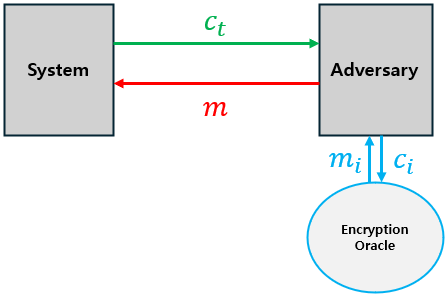
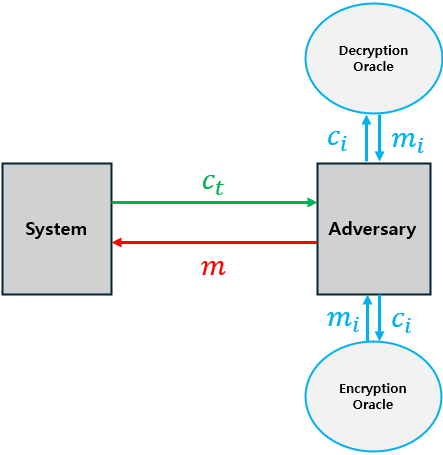
※ CPA랑 CCA에서 Oracle쪽 화살표 잘못그림…
1. Security Game
암호학에서 안전성을 정의하는 방법 중 대표적인 방식은 “Security Game”이라고 불리는 일종의 상황극을 활용하는 방식이다. 이 게임은 Adversary의 조건을 나누고 이를 바탕으로 이 공격자가 암호를 깰 수 있는지를 판별하는 방식으로 진행된다. 이때, 이 게임은 공격자에게 가장 이상적인 상황을 가정하기 때문에, 이 게임에서 안전성을 증명하면 실생활에서도 안전성을 증명할 수 있게 된다.
1) IND-CPA Game
이 게임에서 “암호를 깼다!” 라고 말하기 위해서는 모든 Adversary의 성공 확률(즉, $b’$이 $b$와 같을 확률)이 $50\% (=\frac{1}{2C1})$ 보다 유의미하게 커야한다.
즉, $p[b=b’] = \frac{1}{2} + T(n)$에서 $T(n)$이 negligible function이 아닌 알고리즘이 존재한다면 이 암호문은 깨진 것이다.
반대로 이러한 경우가 존재하지 않으면 IND-CPA Secure라고 판단한다.
예를 들어, 이 암호 알고리즘$(B)$가 인수분해 문제를 기반으로 하고 있다고 하자. 이 경우 non-neglibible function이 없다는 것을 가정할 수 있으므로 안정성을 증명할 수 있다.
반대로 공격자가 만약에 1-bit 정보만이라도 알 수 있다고 한다면 이 암호 체계는 깨진다. 만약에 $m_0, m_1$의 구성을 전부 1이랑 전부 0으로만 해서 System에 전달하면 되기 때문이다.
negligible function
모든 Polynomial function($n + n^2 + n^3 + …$)의 역수(Reciprocal of polynomial$ = \frac{1}{n} + \frac{1}{n^2} + \frac{1}{n^3} + …$)보다 더 빠르게 감소하는 함수
2) IND-CCA Game
마찬가지로 암호 체계까 IND CCA Secure하다는 것은, 어떠한 공격자도 위 알고리즘을 깨는 non-negligible function을 찾을 수 없다는 뜻이다.