5. Propositional Logic

Propositional Logic

1. BackGround

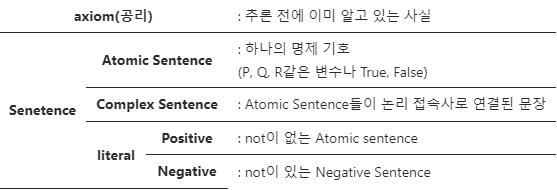
1) 표현

1. Truth Table	실제 표현 가능한 세계들의 모음 (내가 알고있는 사실이 True인지 False인지는 상관없음)
2. Model	실제 표현 가능한 세계들 중 하나 (Truth Table의 한 행)
3. Knowledge Base	에이전트가 알고있는 문장들의 집합 즉, KB가 True라는 말은 현재 알고있는 지식들이 전부 True라는 뜻

---

논리

	설명	예시
Satisfaction $M(\alpha)$	어떤 문장 $\alpha$가 어떤 Model $m$에서 참이면 m이 $\alpha$를 Satisfy한다고 정의 또는 m은 $\alpha$의 Model이라고 정의 (※ 어떤 문장이 Satisfiable하다면 문장을 만족하는 1개의 모델(행)이 존재함)
Entailment $\alpha \models \beta$	$\alpha$가 True면 $\beta$도 항상 True인 Model $= M(\alpha) \subseteq M(\beta)$
Derivation $KB \vdash_i \alpha$	i를 따라가면 $KB$에서 $\alpha$가 참임을 증명가능할 때 (Entail과 다르게 과정을 알려줘야 함)

---

Inference(추론)

Infrerence란 기존 문장들에서 새로운 문장을 추론하는 과정을 말한다.

• Sound
  Inference 알고리즘이 항상 entail한 sentence를 유도할 때.

• Complete
  Inference 알고리즘이 entail한 모든 sentence를 유도할 때.
  즉, KB로부터 알수 있는 True인 문장들은 모두 True라고 유도해야함

(참고: 한줄로 Sound한 알고리즘을 만들기 위해서는, 어떤 문장이 들어와도 모두 False라고 출력하도록 하면 된다.)

(참고: 한줄로 Complete한 알고리즘을 만들기 위해서는, 어떤 문장이 들어와도 모두 True라고 출력하도록 하면 된다.)

2) Clause

Logical Connective

$\neg$	$\wedge$	$\vee$	$\Rightarrow$	$\Leftrightarrow$
Not	Conjunction(and)	Disconjunction(or)	Implies	if and only if

---

Clause : literal의 Disjunction(OR)

	Clause
종류	Goal Clause	Fact	Definite Clause	Horn Clause
Positive literal	0개	1개	1개	0개 or 1개
Negative literal	n개	0개	n개	n개

이때, Definite Clause는 implication으로 바꿀 수 있다.

\[1. \; \neg P \vee \neg Q \vee R \qquad\qquad\qquad\qquad\; definition\\ 2. \; \neg(P \wedge Q) \vee R \qquad Implcation \; Elimination\\ 3. \; P \wedge Q \Rightarrow R \qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\,\]

---

Clonjunctive Normal Forms

• Clause들이 Conjunction($\wedge$)연산들로 연결되어 있는 형태
  ($C_1 \wedge C_2 \wedge … \wedge C_n$)
  • ex. $(P \vee Q) \wedge (Q \vee \neg R \vee S) \wedge P$

모든 Propositional Logic은 의미가 같은 CNF로 변환 이 가능하다.

(아래의 Rule 중 Biconditional Elimination과 Implication Elimination, 드모르간 법칙, 배분법칙을 적절히 사용하면된다.)

3) Rule

Theorem Proving이란 어떠한 규칙을 가지고 KB로부터 새로운 사실을 알아내는 과정을 말한다.

이때, 이 규칙에는 다음이 있다.

---

1. Semantics

True, False를 이야기할 수 있는 도구를 가리키는 단어로 대표적으로 Truth Table이 있다.

$P$	$Q \quad$ |	$\neg P$	$P \wedge Q$	$P \vee Q$	$P \Rightarrow Q$	$P \Leftrightarrow Q$
False	False $\quad$ |	True	False	False	True	True
False	True $\quad$ |	True	False	True	True	False
True	False $\quad$ |	False	False	True	False	Fasle
True	True $\quad$ |	False	True	True	True	True

※ Implies는 P가 False이거나, P와 Q가 모두 True인 관계이다.
(즉, P가 진실을 말했을 때, Q가 거짓인 경우만 False이다.)

---

2. inference rule

새로운 문장을 다음과 같은 규칙을 알아낼 수 있다.

Modus Pones	And Elimination	Logical Equivalence	Example
$\frac{(\alpha \Rightarrow \beta, \alpha)}{\beta}$	$\frac{\alpha \wedge \beta}{\alpha}$	$\frac{\alpha \wedge \beta}{\beta \wedge \alpha}, \frac{\alpha \vee \beta}{\beta \vee \alpha}$ (교환법칙) $\frac{(\alpha \wedge \beta) \wedge \gamma}{\alpha \wedge (\beta \wedge \gamma)}, \frac{(\alpha \vee \beta) \vee \gamma}{\alpha \vee (\beta \vee \gamma)}$ (결합법칙) $\frac{\alpha \wedge (\beta \vee \gamma)}{(\alpha \wedge \beta) \vee (\alpha \wedge \gamma)}, \frac{\alpha \vee (\beta \wedge \gamma)}{(\alpha \vee \beta) \wedge (\alpha \vee \gamma)} $ (분배법칙) $\frac{\neg (\alpha \wedge \beta)}{(\neg \alpha \vee \neg \beta)}, \frac{\neg (\alpha \vee \beta)}{(\neg \alpha \wedge \neg \beta)} $ (드모르간 법칙) $\frac{\alpha \equiv \beta}{(\alpha \models \beta) \wedge (\beta \models \alpha)}$ $\frac{\neg (\neg \alpha)}{\alpha}$ $\frac{\alpha \Rightarrow \beta}{\neg \beta \Rightarrow \neg \alpha}$(대우) $\frac{\alpha \Leftrightarrow \beta}{(\alpha \Rightarrow \beta) \wedge (\beta \Rightarrow \alpha)}$ (★Biconditional Elimination) $\frac{\alpha \Rightarrow \beta}{\neg \alpha \vee \beta}$ (★Implication Elimination)	위에서 $P_{1, 2}, P_{2, 1}$에 함정이 없다는 사실을 알아내보자 1. A에 바람이 불면 주변에 함정이 있음 ⅰ. $B_{1, 1} \Leftrightarrow (P_{1, 2} \vee P_{2, 1})$ ⅱ. $B_{1, 1} \Rightarrow (P_{1, 2} \vee P_{2, 1})$, $\;(P_{1, 2} \vee P_{2, 1}) \Rightarrow B_{1, 1}$ ⅲ. $\neg B_{1, 1} \Rightarrow \neg (P_{1, 2} \vee P_{2, 1})$ 2. A에 바람이 불지 않음 $\neg B_{1, 1}$ 3. $P_{1, 2}, P_{2, 1}$에 함정 X $\neg (P_{1, 2} \vee P_{2, 1})$

Logical Equivalence의 증명 방법은 Truth Table을 그려보면 된다.

---

3. Resolution Rule

	Unit Resolution Rule	Resolution Rule
Rule	$\frac{l_1 \vee … \vee l_{i-1} \vee l_i \vee l_{i+1} \vee … \vee l_k, \qquad m}{l_1 \vee … \vee l_{i-1} \vee l_{i+1} \vee … \vee l_k}$	$\frac{l_1 \vee … \vee l_{i-1} \vee l_i \vee l_{i+1} \vee … \vee l_k, \qquad m_1 \vee … \vee m_{i-1} \vee m_i \vee m_{i+1} \vee … \vee m_n}{l_1 \vee … \vee l_{i-1} \vee l_{i+1} \vee … \vee l_k \quad \vee \quad m_1 \vee … \vee m_{i-1} \vee m_{i+1} \vee … \vee m_n}$
Example	$\frac{P \vee \neg Q, \quad Q}{P}$	$\frac{P \vee Q \vee R, \quad P \vee \neg Q \vee S}{P \vee R \vee S}$

어떤 Clause에서 Complementary관계인 두 literal이 있을 경우 두 Clause를 Factoring할 수 있다.

• Complementary: negate($\neg$)가 있고 없고
• Factoring: Complementary인 literal을 지우고 Disjunction($\vee$) 하는 것

Example

여기서 이번에는 $P_{3, 1}$에 함정이 있다는 것을 확인해 보자 1. {2, 1}에 바람이 불면 주변에 함정이 있다. 　ⅰ. $B_{2, 1} \Leftrightarrow (P_{1, 1} \vee P_{2, 2} \vee P_{3, 1})$ 　ⅱ. $B_{2, 1} \Rightarrow (P_{1, 1} \vee P_{2, 2} \vee P_{3, 1})$ 　ⅲ. $B_{2, 1} \Leftarrow (P_{1, 1} \vee P_{2, 2} \vee P_{3, 1})$ 2. {2, 1}에 바람이 분다. 　ⅰ. $B_{2, 1}$ 　ⅱ. $(P_{1, 1} \vee P_{2, 2} \vee P_{3, 1})$(Modus Pones) 3. $P_{3, 1}$에 함정이 있다. 　ⅰ. $\frac{(P_{1, 1} \vee P_{2, 2} \vee P_{3, 1}), \quad P_{2, 2}}{(P_{1, 1} \vee \neg P_{3, 1})}$ 　ⅱ. $\frac{(P_{1, 1} \vee P_{3, 1}), \quad \neg P_{1, 1}}{P_{3, 1}}$

---

2. Theorem Proving

이제 코드를 직접 만들어 보자

Naive한 방법을 먼저 보고, 그 다음에는 Inference Rule을 사용해서 구현하는 방법, 마지막에는 Resolution Rule만을 사용해서 구현하는 방법을 살펴보자.

1) Model Checking Algorithm(Naive)

def is_entails(KB, a):
    symbol = list(*KB.symbol, *a.symbol)
    return check_all(KB, a, symbols, {})

def check_all(KB, a, symbols, model):
    if symbols.is_empty():
        if model.checkall(KB) == True:
            return (model.checkall(a)==True) 
        else:
            return True
    else:
        p = symbol[0]
        rest = symbol[1:]
        return check_all(KB, a, rest, model.union({p: True})) 
               and 
               checkall(KB, a, rest, model.union({p: False}))

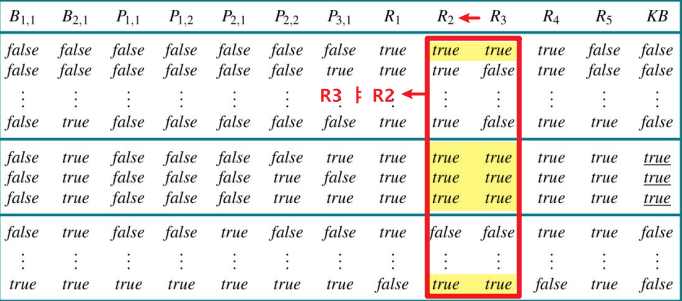
어떤 Knowledge Base(Sentence)가 $\alpha$(Sentence)를 Entail하는지 확인하기 위한 함수를 알아보자.

1. Knowledge Base와 $\alpha$에서 Symbol들을 뽑아낸다.	symbol = list(*KB.symbol, *a.symbol) $\rightarrow$ (A, B, C)
2. 이제 이 Symbol에 True와 False를 넣어가며 Tree를 만든다
3. Tree가 완성되면 각 model에서 a와 KB가 entail한 관계인지 확인한다.

Soundess	Completeness	Time Complexity	Space Complexity
O	O	$O(2^n)$	$O(n)$

2) Forward-Chaining Algorithm(Inference Rule)

def Foward_Chaining(KB, q):
    count = {clause:len(clause.premise.symbol) for clause in KB}
    infered = {sybol:False for symbol in KB.symbol}
    queue = {sybol:False for symbol in KB.fact}

    while not queue.empty:
        p = queue.pop()
        if p == q:
            return true

        if infered[p] == False: # visited 같은 역할
            infered[p] = True
            for clause in KB:
                for premise in clause.premise:
                    if p in premise:
                        count[clause] -= 1
                    if count[clause] == 0:
                        queue.append(clause.conclusion)
    return False

$P \wedge Q \Rightarrow R$을 알고있고(Knowledge Base에 존재),
$P$가 True이고 $Q$가 True라는 것을 알았다고 하면 $R$이 True라는 것을 알 수 있다.

이를 통해 Horn Clause로만 이루어진 Knowledge Base에서 $\alpha$가 참인지 거짓인지 알아보자.

count[s]	Inferred[p]	queue
s라는 Clause에서 Premise중 사실여부를 모르는 Symbol의 개수 ($P\Rightarrow Q$일 때, P:premise, Q:Conclusion)	p라는 Symbol의 True여부 (초기값: 전부 False)	Fact들의 집합 (초기값: KB에서 True인 것)

---

초기화 　　Input: Horn Clause로만 이루어진 Knowledge Base
1번째 Loop 　　ⅰ. Queue에서 A를 꺼낸다. 　　ⅱ. A는 진실이므로 A가 포함된 Clause의 Count를 하나 줄인다.
2번째 Loop 　　ⅰ. Queue에서 B를 꺼낸다. 　　ⅱ. B가 포함된 Clause의 Count를 하나 줄인다. 　　ⅲ. Count가 0이된 Clause의 Conclusion인 L을 Queue에 넣는다.
3번째 Loop 　　ⅰ. Queue에서 L를 꺼낸다. 　　ⅱ. L이 포함된 Clause의 Count를 하나 줄인다. 　　ⅲ. Count가 0이된 Clause의 Conclusion인 M을 Queue에 넣는다.
마지막 Loop 　　ⅰ. Queue에서 L를 꺼낸다. 　　ⅱ. L이 포함된 Clause의 Count를 하나 줄인다. 　　ⅲ. Count가 0이된 Clause의 Conclusion인 M을 Queue에 넣는다.

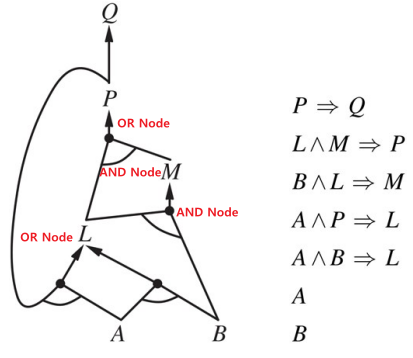
Soundess	Completeness
O	O (Imply이기 때문에 False가 있어도 하나만 True면 True)

---

Backward-Chaining Algorithm

위와 같이 AND-OR Search Tree를 사용해 구현 가능하다.
즉, Goal을 Root Node로 생성해 시작하자.

Soundess	Completeness
O	x

3) Resolution(분해)

def resolution(KB, a):
    clause = conjunction(KB, not a).to_CNF()
    new = {}

    while True:
        for i in range(len(clause)):
            for j in range(len(clause)):
                if i != j:
                    resolvents = resove(clause[i], clause[j])   #ex. P V not Q, Q --> P
                    if resolvents.is_empty():                   #ex. if P V not P --> {}
                        return True
                    new.union(resolvents)
        if new in clauses: # 자기자신이 되었을 때
            return False
        clauses = clauses.union(new)

Knowledge Base에 Definite Clause가 아닌 CNF만 들어있을 경우 사용하는 방법이다.

이때, 모든 Sentence는 CNF로 변형이 가능하므로 이 Resolution은 모든 Sentence에 대해 사용이 가능하다.

Resolution은 다음과 같은 증명에 의해,
$KB \models \alpha$임을 알아내기 위해서 $KB \wedge \neg \alpha$가 Satisfiable하지 않음을 확인한다.
(즉, $KB \wedge \neg \alpha$를 만족하는 Model이 하나도 존재하지 않다는 것을 확인)

Validity

항상 True인 문장은 Valid하다고 정의된다. ⅰ. $\alpha$가 Satisfiable $(\overset{동치}{=}) \neg \alpha$는 not Valid ⅱ. $\alpha$가 Valid $(\overset{동치}{=}) \neg \alpha$는 not Satisfialbe ⅲ. $\alpha \models \beta \quad (\overset{동치}{=}) \quad \alpha \Rightarrow \beta$가 Vaild ★. $\alpha \models \beta (\overset{동치}{=}) \alpha \wedge \neg \beta$가 Unsatisfialbe

$P \vee \neg P$

---

1. 초기화	ⅰ. KB, Query 　　$KB:\quad B_{1, 1} \Leftrightarrow (P_{1, 2} \vee P_{2, 1}), \quad \neg B_{1, 1}$ 　　$Query(\alpha): \quad \neg P_{1, 2}?$ ⅱ. Clause 　　$(B_{1, 1} \Leftrightarrow (P_{1, 2} \vee P_{2, 1})) \wedge (\neg B_{1, 1}) \wedge \neg (\neg P_{1, 2})$ 　　$\equiv (\neg B_{1, 1} \vee (P_{1, 2} \vee P_{2, 1})) \wedge (\neg(P_{1, 2} \vee P_{2, 1}) \vee B_{1, 1}) \wedge (\neg B_{1, 1}) \wedge P_{1, 2}$ 　　$\equiv (\neg B_{1, 1} \vee (P_{1, 2} \vee P_{2, 1})) \wedge (\neg P_{1, 2} \vee B_{1, 1}) \wedge (\neg P_{2, 1} \vee B_{1, 1}) \wedge (\neg B_{1, 1}) \wedge P_{1, 2}$
2. 임의의 2개를 　Resolution
3. Empty Clause가 　나올 때 까지 　반복	ⅰ. EmptyClause 　　Empty Clause가 나왔다는 것은 $KB \wedge \neg \alpha$가 Unsatisfialbe이라는 뜻이다. 　　즉, 주어진 Query(\alpha)는 $KB \models \alpha$로 참인 문장이 된다. 　　(ex. Resolution($P, \neg P$)일 경우) 　ⅱ. Empty Clause가 아닐경우 　　Empty Clause가 없다는 것은 모순이 없다는 뜻이고, 즉 $KB \wedge \neg \alpha$가 참이라는 뜻이다

---

Result

이 Resolution은 2번 방법과는 다르게 다음과 같은 장점이 있다.

• Resolution Rule하나만 사용하면 된다.
• Sound하면서 Complete한 결과를 만든다.