7. PQC(ECC & Lattice)
1. Elliptic Curve
Elliptic Curve는 다음과 같이 정의한다.
- Field K 위의 타원 곡선은 변수가 2개인 Non-Singular 3차 곡선이고, Rational Point를 하나 이상 가진다.
(Non-Singular: 매끄러워서 미분 가능 함, Rational Point: 정의된 숫자 시스템(Field K)에 존재하는 점이 최소 하나(e.g. $\mathcal{O}$))
이 Elliptic Curve의 핵심은 이 타원위의 점들을 가지고 “덧셈”이라는 연산을 새롭게 정의하고, 이를 통해 풀기 어려운 문제를 ‘정의’하는 것이다.
Elliptic Curve상에서 덧셈은 다음과 같이 정의된다.
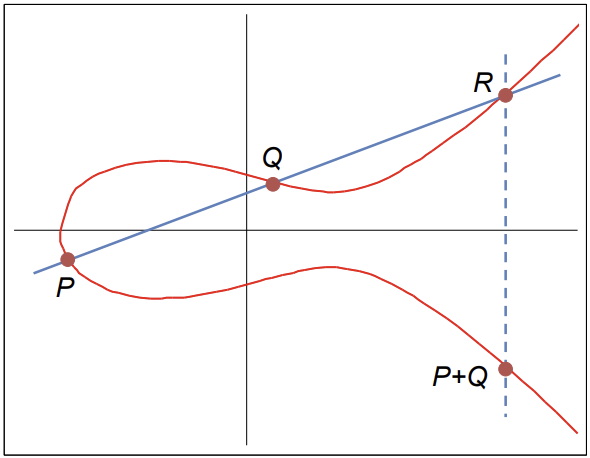
덧셈($P + Q$): 곡선 위의 두 점 $P$와 $Q$를 지나는 직선을 그으면, 이 직선은 곡선과 또 다른 한 점 $R$에서 만난다. 이 교점 $R$을 x 축에 대칭시킨 점을 $P + Q$라고 정의한다.
무한 원점(Point at Infinity): Elliptic Curve에서의 원점은 무한원점($\mathcal{O}$)으로 Elliptic Curve상에서의 수학적 법칙을 완성하기 위해 가상으로 정의한 점이다. 만약 P와 Q를 지나는 직선이 x축과 수직이라면 Elliptic Curve와 만나는 점이 실재로는 존재하지 않을 것이다. 하지만, 수학적 일관성을 유지하기 위해 무한대에서 만나는 점이 있다고 가정하고, 이를 무한 원점이라고 정의한다.
가환군(Commutative Group, Abelian Group): 위 덧셈 법칙을 통해 Elliptic Curve 위의 점들은 가환군을 이룬다. 즉, 교환 법칙이 성립한다.
ⅰ) (덧셈의 항등원) $P + \mathcal{O} = \mathcal{O} + P = P$
ⅱ) (Inverse 정의) $P + (-P) = \mathcal{O}$
ⅲ) (결합 법칙) $(P + Q) + R = P + (Q + R)$
ⅳ) (교환 법칙) $P + Q = Q + R$
ⅴ) 덧셈연산에 대해 닫혀있음(더해도 같은 Elliptic Curve안의 점으로 정의됨)
※ $P = (x, y)$
※ $-P=(x, -y)$
※ 수식($(x_3, y_3) = (x_1, y_1) + (x_2, y_2)$)
\(m = \begin{cases}\frac{y_1 - y_2}{x_1 - x_2}, x_1 \neq x_2 \ \\ \frac{3ax_1^2 + 2bx_1 + c}{2y_1}, x_1 = x_2\end{cases}\)
$x_3 = \frac{1}{a}(m^2 - b) - x_1 - x_2$
$y_3 = -m(x_3 - x_1) - y_1$
1) Discrete Logarithm Problem(이산 대수 문제)
| DLP | ECDLP |
|---|---|
| 어떤 수 $a, b, p$가 주어졌을 때, $a^x \equiv b \pmod p$를 만족하는 가장 작은 양의 정수 x를 찾는 문제 | Elliptic Curve상의 점 $P, Q$와 scalar $x$가 주어졌을 때,$xP \equiv Q \pmod p$를 만족하는 $x$를 찾는 문제 |
또한 암호학적 연산이 성립하기 위해서 숫자들이 노는 ‘공간’이 정의되어야 한다. 즉, 유한체(Finite Field)에서 정의되는데, 이는 원소의 개수가 유한한 Field(체)를 의미한다. 이러한 유한체를 정의하기 위해서는 주로 Modulo 연산을 사용한다. 예를 들어, $(x, y)$가 있을 때, $x$와 $y$ 모두 $\bmod P$안에서 (0, 1, … , P) 정의하는 방식이다. 이를 활용해 컴퓨터 알고리즘으로 ECDLP 문제를 만들 수 있다.
난이도
ECDLP는 Factorization 문제보다 훨씬 어려운 문제이다. 즉, 더 적은 수의 bit를 사용해서도 Factorization 문제와 같은 난이도의 보안성을 갖출 수 있다.
Bit Security($2^n$) RSA ECC 80 1248 160 128 3248 256 256 15424 512
2) ECDSA
이전에 Elgamal을 활용해 DSA Signature를 만들 수 있었듯이, ECDSA를 활용해서도 전자 서명을 만들어낼 수 있다.
먼저, 사용하는 파라미터는 다음과 같다.
| Curve | Base point($G$) | order($n$)) |
|---|---|---|
| 사용할 타원체 | 곡선 위 기준점 | $n \times G = \mathcal{O}$인 정수 |
파라미터라는 것은, 예를 들어 secp256k1이라는 ECDSA를 사용할 경우 $y^2 = x^3 + 7$이라는 타원체를 사용하기로 약속되어 있다는 뜻이다.
Generation
- 개인키($d_A$): 1부터 n-1 범위의 무작위 정수
- 공개키($Q_A$): $Q_A = d_A \times G$ 계산 결과로 나온 곡선 위의 점
이후 메시지(m)의 HASH값(e)의 가장 왼쪽 $L_n$비트를 가져와 정수(z)로 만든다.
- $k$선택: [1, n-1]에서 암호학적으로 안전한 임의의 정수 k를 선택
- $(x_1, y_1) = k \times G$
- $r = x_1 \pmod n$
- $s = k^{-1}(z + r \cdot d_A)\pmod n$
이후 $(r, s)$를 전자서명으로 활용할 수있다.
Verification
이제 공개키를 활용해 해당 서명 $(r, s)$가 유효한지 확인해보자. (일단, $(r, s)$가 [1, n]사이의 정수인지 확인하고, 아니면 유효하지 않은 서명이다.)
우선 서명생성과정과 마찬가지로 메시지(m)의 HASH값(e)의 가장 왼쪽 $L_n$비트를 가져와 정수(z)로 만든다.
- $u_1 = z \cdot s^{-1} \pmod n$
- $u_2 = r \cdot s^{-1} \pmod n$
- $(x_1, y_1) = u_1 \times G + u_2 \times G$
이제, $r \equiv x_1 \pmod n$이 맞는지 확인
2. Lattice
RSA나 ECC가 정수론에 기반했다면, Lattice(격자 암호)는 기하학적인 공간 문제에 기반한다.
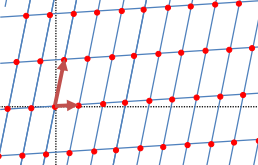
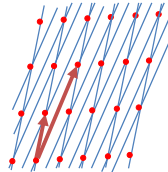
먼저 격자란 공간 상에 규칙적으로 배열된 점들의 집합이다. 이 점들은 기저벡터들을 더하거나 빼서 만들어지는 평행 사변형의 꼭짓점들로 이해할 수 있다.
1) Closest Vector Problem
위의 격자 암호가 성립할 수 있는 문제는, CVP(Closest Vector Problem)이라는 문제가 풀기 어렵다는 점 때문이다.
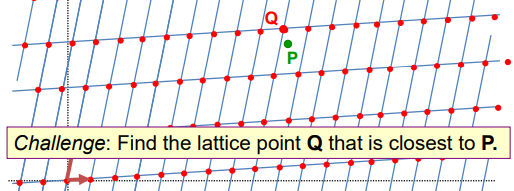
- 문제: 격자 공간 위의 점 P가 주어졌을 때, 그 점 P와 가장 가까이 있는 격자점 Q를 찾는 문제
- 어려움: 2차원 평면에서는 이게 쉬워보이지만, 차원이 높아지고 기저 벡터가 복잡해지면 계산이 기하급수적으로 어려워진다.
Key 구성 원리
이 시스템은 동일한 격자 점들을 표현하는 서로 다른 두가지 방법이 있다는 점을 이용한다.
Public Key Private Key 짧고 직교에 가까운 기저벡터 길고 찌그러진 기저벡터 이 기저로는 CVP문제를 쉽게 풀 수 있음 이 기저로는 가장 가까운 점이 어디인지
찾기 어려움
2) 특징
- Pairing 가능: ECC와 마찬가지로 쌍연산성(Bilinearity) 성질을 만족시킨다.($E(aP, bQ) = e(P, Q)^{ab}$)
- 완전 동형 암호: 암호화된 데이터끼리 덧셈뿐만 아니라 곱셈까지 가능하다.($E(M_1) \times E(M_2) = E(M_1 \times M_2)$)
- 양자 내성: ECC와 RSA와는 다르게 CVP를 푸는 문제는 양자 알고리즘을 사용해도 지수시간이 걸린다.