포스트

Positional Encoding

게시
By UI-JIN KIM 26 분읽는 시간

공부 이유: 자연어, 비전, 오디오 등 각 도메인에서의 특징에 따라 Positional Encoding방식을 다르게 해야하지 않을까?

  • 자연어: 1D Signal, Context의 길이가 매우 중요. Extrapolation(훈련 중에 본 것보다 더 긴 길이의 시퀀스를 처리하는 능력)이 중요
  • 이미지: 2D Signal, 2차원적인 공간 정보가 중요(중복된 정보가 많으니, 이를 고려할 필요가 있을 듯)
  • 오디오: 1D Signal, 1차원이지만 주파수 도메인으로 변환할 때, 시간 축이 사라짐
  • 비디오: 3D Signal, 2차원 적인 공간정보가, 순서에 따라 존재.
  • 멀티모달: ND Signal

요약: Positional Encoding에 관한 연구는 주로 LLM의 외삽(Extrapolation)능력을 향상시키기 위해 진행되었다.
외삽이란, 훈련과정에서 보지 못했던 훨씬 더 긴 문장들에서도 잘 동작하는 능력을 말한다. 기존에 사용하던 APE는 각 토큰별 절대적인 값을 갖도록 한 채 학습하는게 목표였기 때문에, 다른 토큰과의 상호작용을 할 때, 불리하다는 단점이 있다. 이를 보완하기 위해 RPE라는 개념이 등장했고, 다른 토큰들과의 상대 위치를 학습하여 외삽 능력을 기를 수 있도록 하는 방식으로 발전하였다.

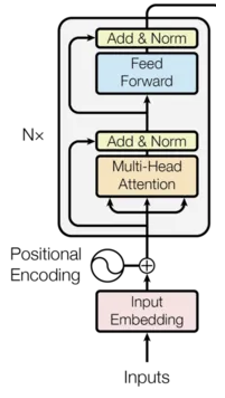
기존의 RNN은 순차적으로 입력 데이터를 처리하였다. 하지만 Transformer의 경우 입력되는 데이터를 순차적으로 처리하는 것이 아닌, 한번에 병렬로 처리한다는 특징이 있다. 이러한 특징으로 인해 병렬 처리를 할 수 있지만, 입력된 순서에 대한 정보가 사라진다는 단점이 있다.(Permutation Equivariant) 이러한 문제를 해결하기 위해 Positional Encoding이라는 개념을 도입하였다.

ⅰ) Positional Encoding의 필요조건

  1. 불변성
    입력 값의 특징(길이 등)에 따라 달라져서는 안됨
  2. 절대성
    distance를 표현하기 위해 각 위치마다 서로 다른 값을 가져야 함
  3. 선형 연산 표현
    distance를 선형 연산으로 표현할 수 있어야 함.
  4. 학습 가능성 (Gradient Descent를 이용하여 학습할 경우)
    • PE의 값이 빠르게 증가하면 안됨 → Gradient Expoding 발생
    • PE의 값이 입력값에 비해 너무 크면 안됨 → 입력값의 왜곡 발생

예시)

  • (간단) [0, 1, 2, 3, 4, 5, 6, 7]
    학습 불가능(입력값에 비해 크고 빠르게 증가함)
  • (정규화) [0, 0.14, 0.29, 0.43, 0.57, 0.71, 0.86, 1]
    입력 값의 길이에 따라 인코딩 값이 달라짐
  • (벡터 형태) [000, 001, 010, 011, 100, 101, 110, 111]
    Distance로써 이용 불가능(dist(000, 001) != dist(011, 100) )

※ CNN에서 Padding은 Position 정보를 암묵적으로 학습할 수 있도록 도와준다는 연구가 있다.

※ CoordConv, Spatial Broadcast Decoder, HANet라는 논문들을 보면 Convolution 연산에 위치 정보를 직접적으로 제공해 주기 위해 예시 2번과 같은 PE를 사용해준다. 이는 Attention 과 달리 보통의 Convolution 에서는 입력 이미지의 크기가 항상 같다고 가정하기 때문에 1번 조건을 고려할 필요가 없었을 것이다. (+ 만약, regression이나 classification이 아닌 이미지 생성을 위해 CoordConv를 사용하면 문제가 될 수 있을 것 같다.)

우리는 위를 만족하는 PE를 단순하게 입력 시퀀스에 더해줌으로써, Transformer의 Permutation Equivariant한 특성을 제거할 수 있다.

그렇다면 이제, ⅰ) Concat이 아닌 Element-Wise Sum만으로도 PE가 어떻게 가능한지, ⅱ) 모델이 이러한 임베딩이 PE임을 어떻게 알 수 있는지가 궁금해 진다. (참조)

ⅱ) Positional Encoding의 원리

Attention에서는 기본적으로 두 개의 단어 임베딩(x, y)에 대해 쿼리 변환, 키 변환을 수행한 후 내적을 통해 유사도를 비교한다. 즉, Attention에서는 아래의 식과 같이 y를 x의 공간으로 매핑하는 $Q^TK$ 행렬을 학습하는 것이 목적이라고 생각할 수 있다.

\[(Qx)^T \cdot Ky = x^T \cdot (Q^TKy)\]

이때, 위치 인코딩 e와 f를 x와 y에 추가한다는 것은 다음과 같다.

\[\begin{align} & (Q(x+e))^T \cdot (K(y+f)) \\ & = (Qx + Qe)^T \cdot (Ky + Kf) \\ & = (Qx)^T Ky + (Qx)^T Kf + (Qe)^T Ky + (Qe)^T Kf \\ & = x^T (Q^TKy) + x^T(Q^TKf) + e^T(Q^TKy) + e^T(Q^TKf) \\ \end{align}\]

즉, 위와 비교해 보았을 때, $x^T(Q^TKf) + e^T(Q^TKy) + e^T(Q^TKf)$라는 항이 추가된 것을 알 수 있다. 이는 단순히 덧셈으로도 변환 행렬 $Q^TK$가 단어 임베딩 x와 y사이의 관계 이외에도, x와 f, e와 y, e와 f 사이의 관계를 고려할 수 있도록 학습된다는 것을 알 수 있다. 즉, Attention 전에 PE를 더해주는 것 만으로도 e와 f의 관계를 이용할 수 있게 된다.

그렇다면 이제 학습 단계에서 x + e단계에서 “원래의 단어 정보가 사라지는 것은 아닐까?” 혹은, “모델이 이를 어떻게 분리해서 이해할 수 있을까?” 라는 의문이 들 수 있다.

고차원 공간에서는 특이한 성질이 발생하는데, 바로 차원이 클수록 무작위로 뽑은 두 벡터는 거의 직교한다는 것이다. 따라서 단어 임베딩과 위치 임베딩은 독립적으로 초기화 되고, 학습 과정에서 크게 섞이지 않고 독립적으로 활용될 수 있다.

따라서, concat방식이 아닌 add로도 효과적으로 위치정보를 활용할 수 있게 만들 수 있고, 심지어 parameter 효율적으로도 설계할 수 있다.

Positional Encoding의 종류

1. APE(Absolute Positional Encoding)

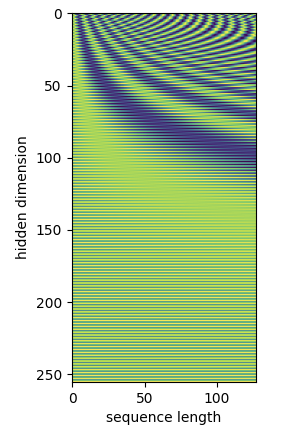
1) Sinusoidal PE

\[\begin{align} & PE_{(pos, 2i)} = \sin(\frac{\text{pos}}{10000^\frac{2i}{d_{model}}}) \\ & PE_{(pos, 2i+1)} = \cos(\frac{\text{pos}}{10000^\frac{2i}{d_{model}}}) \\ \end{align}\]

4번 조건(완만, 작은 수)을 만족시키는 가장 간단한 함수를 생각해 보면, Sign Function을 생각할 수 있다.

\[A \sin(Nx)\]
  • A가 작을 경우: 크지 않은 값 선택 가능
  • N이 작을 경우: 주기가 길어져 완만한 값과 중복되지 않는 값 선택 가능 (논문에서는 1/10000)

하지만 이 sign함수를 그대로 사용할 경우 3번 조건(선형 연산 표현)을 만족시킬 수 없다. 이를 위해 Cosine Function과 함께 다음 성질을 만족하도록 만들 수 있다.

\[PE(x + \Delta x) = T(\Delta x) \cdot PE(x) \\ ㅤ\\ \begin{bmatrix} \cos(x + \Delta x) \\ \sin(x + \Delta x) \end{bmatrix} = \begin{bmatrix} \cos(\Delta x) & -\sin(\Delta x) \\ \sin(\Delta x) & \cos(\Delta x) \end{bmatrix} \begin{bmatrix} \cos(x) \\ \sin(x) \end{bmatrix}\]

(※ 위는 PE의 Dimension을 2라고 할 때의 예시이고, Dimension이 늘어나도 변환 행렬을 대각행렬로 만들어 같은 방식으로 확장이 가능하다.)

즉, $PE(x + \Delta x) - PE(x) = (T(\Delta x) - 1) \cdot PE(x)$ 이므로 선형변환 식으로 PE에서 차이를 선형 변환으로써 정의 할 수 있다.

예시)

alt textalt text

단점

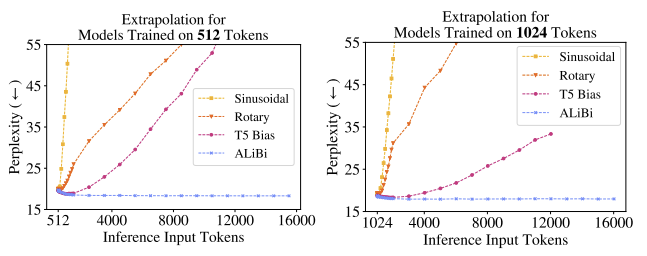
  • Extrapolation 능력이 약함 (ALiBi 논문에서 실험과 함께 언급)

2) Learnable

Transformer 논문에서는 위의 Positional Encoding Vector를 Learnable한 Parameter로 설정해 학습하는 방식도 제안되었다. 하지만 성능에서 별다른 차이를 가져오지 못했다고 한다.

※ 하지만 이는 특정 경우에 한해서이고, 시퀀스가 길어지거나 데이터 셋의 상황에 따라 Sinusoidal 방식이 더 좋은 성능을 가져오기도 한다.

2. RPE(Relative Positional Encoding)

1) RPE(Relative Positional Encoding)

Transformer는 구조적으로 위치 정보를 명시적으로 모델링하지 않았다. 따라서 기존 논문에서는 APE를 사용해 각 토큰의 위치마다 고유의 값 (sinusoidal)을 부여하거나 learnable한 값을 부여하였다. 하지만, 이 중 learnable한 방식을 사용할 경우 학습 도중 보지 못한 긴 시퀀스 길이에 대한 일반화가 제한적이라는 단점이 있었다.

이를 보완하기 위해 토큰마다 PE를 적용하는 방식이 아닌, Attention 계산 시 토큰 간 상대적인 위치를 계산할 수 있도록 도와주는 방식을 제안하였다.

APERPE
alt textalt text
토큰에 위치값 부여Attention시 위치 값 부여
\(x'_{ij} = x_{ij} + PE_{ij} \\ e_{ij} = \frac{(x'_iW^Q)(x'_jW^K)^T}{\sqrt{d_z}} \\ a_{ij} = \frac{e^e_{ij}}{\sum^n_{k=1} e^e_{ik}} \\ z_i = \sum_{j=1}^n a_{ij}(x'_jW^V)\)\(PE^K_{ij} = W^K_{pe} |_{clip(j-k, k)} \\ PE^V_{ij} = W^V_{pe} |_{clip (j-i, k)} \\ e_{ij} = \frac{(x_iW^Q)(x_jW^K + PE^K_{ij})^T}{\sqrt{d_z}} \\ z_i = \sum_{j=1}^n a_{ij}(x'_jW^V + PE^V_{ij})\)

※ $clip(x, y) = \max(-y, \min(y, x))$: 특정 거리 이상에서는 distance가 크게 의미있게 동작하지 않다라는 가설 하에 사용.

2) RoPE(Rotary Positional Encoding)

alt text

참고할 만한 블로그 글

Background

APE의 경우 문장을 평행이동할 경우 값이 달라진다. 즉 $p_n, p_m \rightarrow p_{n+c}, p_{m+c}$일 경우 두 distance사이의 값이 달라진다. 이를 보완하기 위해 Relative Positional Encoding들이 등장했다.

  • RPE
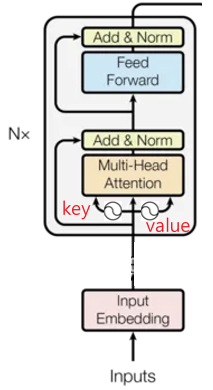
    K, Q, V를 한번에 Encoding했던 APE와 달리, K와 V에만 각각 learnable한 Weight를 더해주는 방식으로 Q와의 상대 위치 계산
  • Transformer-XL
    K, Q를 Attention하는 과정을 수식으로 풀고, 여기에 상대 위치 도입
    ㅤ
    $(W_q(x_m + p_m))^T (W_k(x_k + p_n)) = x_m^T A x_n + x^T_m B p_n + p^T_m C x_n + p^T_m D p_n$
    ⅰ) 두번째 세번 째 항은 각각 절대 위치에만 의존하게 된다.
    ㅤ
    ⅱ) $p_n$을 $p_{m-n}$으로 상대화 하고, 이 경우에 $p_m$은 절대 위치가 되므로 $u, v$같은 학습 벡터 사용하여 보완
    $\rightarrow \quad x_m^T A x_n + x^T_m B p_{m-n} + u^T C x_n + v^T D p_{m-n}$
  • T5, DeBERTa
    Transformer-XL의 변형들

정리하자면 위치 정보를 주입하기 위해 기존에는 “더하는”방식을 사용하였다. 하지만 이 방식을 사용하면 Transformer-XL과 같이 절대 위치에 해당되는 항을 없애기 위해, 복잡하고 번거로운 설계가 필요하다. 즉, RPE에 적합하지 않은 설계이다.

Problem Definition

  1. Flexibility of length
    Learnable APE는 학습 시 사용했던 길이에 한해서만 제대로 동작했고, RPE에서는 이를 어느정도 보완하긴 했지만 결국 어느정도 길이 이상에서는 Cliping하는 방식을 사용한다.
  2. Decaying intertoken dependency
    사실 기존의 RPE에서는 상대 위치를 고려하는 것이 distance가 길어질 때 의존도가 줄어든다는 것을 보장하지 않았다. 단순히 상대 위치에 대한 임베딩을 학습하는 방식으로 진행했기 때문이다.
  3. Capability of equipping the Linear self-attention
    기존의 RPE는 softmax 기반의 quadratic($O(N^2)$ 시간복잡도) self-attention을 전제로 설계되어 있었기 때문에, 최근 제안된 Linear self-attention 구조와는 직접적으로 결합하기 어려웠다.

Approach

덧셈이 아닌, 회전 곱을 이용하면 Attention과정에서 자동으로 상대 위치만 고려하도록 변환이 된다.
예를 들어, $\mathbf{x}$를 word embedding을 거친 input vector, $f(x)$를 positional embedding 함수라고 했을 때, 기존의 방식들은 다음과 같이 정의 할 수 있다.

  • Sinusoidal Positional Embedding
    $f_{t: t\in [q, k, v]}(x_i, i) := \mathbf{W}_{t:t\in [q, k, v]} (x_i + p_i)$
  • Relative Positional Embedding
    $f_q(x_m) := \mathbf{W}_q x_m$
    $f_k(x_n, n) := \mathbf{W}(x_n + \tilde{p}^k_r)$
    $f_v(x_n, n) := \mathbf{W}(x_n + \tilde{p}^v_r)$

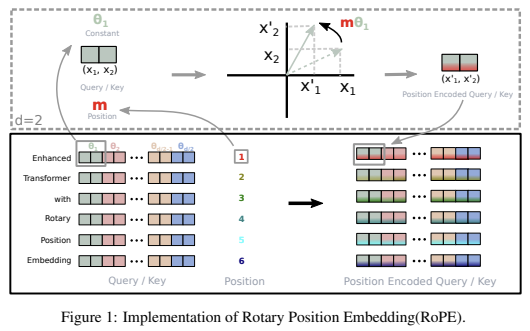
반면에 RoPE에서는 덧셈으로 위치정보를 주입하는 것이 아닌 곱셈을 이용한다.

  • Rotary Positional Embedding
    \[f_{\{q,k\}}(x_m, m) = (W_{\{q, k\}} x_m)e^{im\theta} = R^d_{\Theta, m} W_{\{q, k\}} x_m \\ = \begin{bmatrix} \cos(m\theta_1) & -\sin(m\theta_1) & 0 & 0 & ... & 0 & 0 \\ \sin(m\theta_1) & \cos(m\theta_!) & 0 & 0 & ... & 0 & 0 \\ 0 & 0 & \cos(m\theta_2) & -\sin(m\theta_2) & ... & 0 & 0 \\ 0 & 0 & \sin(m\theta_2) & \cos(m\theta_2) & ... & 0 & 0 \\ 0 & 0 & 0 & 0 & ... & \cos(m\theta) & -\sin(m\theta_l) \\ 0 & 0 & 0 & 0 & ... & \sin(m\theta) & \cos(m\theta_l) \\ \end{bmatrix} W_{\{q, k\}}x_m\]

즉, $e^{i\theta} = \cos \theta + i \sin \theta$로 정의되는 Euler 공식을 활용한다.
이 경우 $q_m^T k_n = (R^d_{\Theta, m} W_q x_m)^T (R^d_{\Theta, n} W_k x_n) = x^T W_q R^d_{\Theta, n-m} W_k, x_n$ 이 되기 때문에, 기존의 방식과 달리 절대 위치항이 존재하지 않아 상대 위치만을 가지고 계산을 쉽게 할 수 있다.

이때, Sinusoidal PE와 마찬가지로 2쌍씩 짝을 지어 각도를 계산하고 각 쌍마다 서로 다른 회전 속도($\theta_i = 10000^{\frac{-2i}{d}}$)를 준다.

APE와 다른 점

  • key와 query에만 해당 정보 주입 $\rightarrow$ value는 position 정보를 활용하지 않기 때문에 최종 output에는 명시적 position 정보가 없음
  • initial layer가 아닌, every layer마다 PE 주입

Analysis

이 논문을 보고 든 생각들…

  • 주기성을 갖기 때문에 발생하는 문제들
    • 매우 큰 토큰 길이를 갖는 문장($2 \pi$)에서는 다시 비슷한 각도로 회귀하는 현상이 발생할 수 있을 것 같다.
    • 매우 큰 토큰 길이를 갖는 문장은 음의 방향에 존재하는 토큰과 비슷한 각도차이가 발생하는 경우가 있을 것 같다.

  • Dot Product에서 토큰간 PE를 비교해 위치 정보를 활용한다고 가정하고, 여기서 미치는 영향에 대해서만 논의했던 것 같다.
    하지만 이 외에도 Rotary로 바꿈으로써 Multi-head구조, Layer Normalization, Residual Connection 등에서 어떤 영향이 없을지에 대해서도 생각해볼 필요가 있을 것 같다.

  • long term decay가 적용되어야 하는 것은 맞는 것 처럼 보이긴 한데, 꼭 그렇지만은 않은 경우도 있을 것 같다.
    (Multi-head 활용 방안?)

3) ALiBi

Background

Transformer는 입력 길이 $L$에 맞춰 학습되고, 보통 $L_{valid} > L$인 긴 시퀀스에서는 Extrapolation 성능이 떨어진다.
기존에 가장 많이 쓰이던 Sinusoidal PE는 이론상 무한 확장이 가능할 줄 알았으나, 실제 실험에서는 $L + 20 \sim 50$ 정도까지만 유효하고 이후 성능이 급격히 저하되었다.

이러한 문제를 해결하기 위해 RPE, RoPE 등 다양한 방식이 제안되었다.

Problem Definition

alt text

이에 본 논문에서는 Extrapolation을 위한 실험을 구성하여 진행하였고, 기존의 PE들을 비교해본 결과 한계가 있다는 것을 발견하였다. (위 그릠 참조)

 RotaryT5 Bias
설명ⅰ) Attention Score 계산
$\quad : E = PE_q(Q)^TPE_k(K)$
ⅱ) Attention Distribution 계산
$\quad : AD = Softmax(E)$
ⅲ) Attention Value 계산
$\quad : AV = AD \cdot V$		ⅰ) Attention Score 계산
$\quad : E = Q^TK $
ⅱ) Bias 추가
$\quad : E’ = E + B$
ⅲ) Attention Distribution 계산
$\quad : AD = Softmax(E’)$
ⅳ) Attention Value 계산
$\quad : AV = AD \cdot V$
유효 거리$\sim + 200$ Token$\sim + 800$ Token
단점학습/추론 속도 느려짐학습 속도가 2배 이상 느려짐
메모리 사용량 증가

Approach

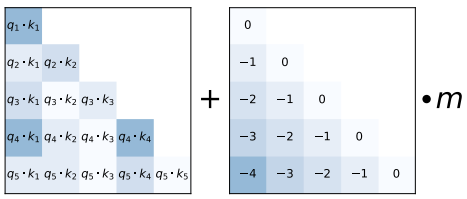
alt text

ALiBi는 기존 Transformer와 달리 임베딩 단계에서 위치 정보를 추가하지 않고, Attention Score 계산 단계에서 Query-Key 내적 결과에 거리 기반의 선형 bias를 직접 추가한다.

  • Attention Score 계산
    $\quad E = QK^T$
  • Bias 추가 (head별 slope 적용)
    $\quad E’ = E + m \cdot [- (i-1), …, -2, -1, 0]$
    (여기서 $m$은 head별로 고정된 slope 값)
  • Attention Distribution 계산
    $\quad AD = Softmax(E’)$
  • Attention Value 계산
    $\quad AV = AD \cdot V$

이때 slope $m$은 학습되지 않고, head별로 미리 정해진 기하수열(geometric sequence)로 설정된다. 예를 들어, 8-head 모델에서는 $m \in {\tfrac{1}{2^1}, \tfrac{1}{2^2}, …, \tfrac{1}{2^8}}$ 을 사용한다.

특징

  • 멀리 떨어진 토큰일수록 점수가 선형적으로 패널티를 받는다 (recency bias).
  • head마다 다른 기울기를 가지므로, 일부 head는 장거리 의존성도 유지 가능하다.
  • slope를 학습 가능하게 바꿔봤지만 extrapolation 성능은 오히려 떨어지고, 학습 속도도 3% 느려졌다. 따라서 slope는 고정값으로 두는 것이 최적이었다.
  • Position 정보는 RoPE/T5 Bias처럼 Q, K에는 들어가지만 V에는 들어가지 않는다.

4) YaRN

Background

ALiBi에서 RoPE의 Extrapolation에 대한 한계가 지적되었지만, 이러한 점을 보완하기 위한 여러 후속 논의도 여러 커뮤니티에서 있었던 것 같다.(Reddit)
대표적인 RoPE의 한계는 실제로 학습한 길이를 넘어가면 Attention Score가 왜곡되는 문제이다. 예를 들어 RoPE가 2048 토큰까지 학습 했다면, 4096 같은 긴 길이의 입력이 들어오면 $e^{im\theta}$의 위상이 겹쳐지는 경우가 발생하기 때문이다. 이를 해결하기 위해 여러 종류의 RoPE Scaling 기법들이 제안되었다.

이 논문에서는 먼저 이러한 논의들을 하나의 수식으로 정리하고, 기존 방식들의 문제점을 정의한다.

Positional Encoding함수 $f’_W(x_m, m, \theta_d) = f_W(x_m, g(m), h(\theta_d))$를 Scaling함수를 활용해 다음과 같이 표현할 수 있다.

Linear InterpolationNTK-aware ScalingDynamic NTK Scaling
$g(m) = \frac{L_{\text{train}}}{L_{\text{infer}}} \cdot m$$g(m) = \alpha \cdot m$ (고정값)$g(m) = [ \alpha \cdot \tfrac{L_{\text{cur}}}{L_{\text{train}}} - (\alpha-1) ] \cdot m$
학습 길이를 넘어서는 위치를
비율로 압축		Attention kernel 분포가
학습 시와 유사하도록 조정		시퀀스 길이에 따라 α를
동적으로 업데이트
($L_{\text{cur}}$은 현재까지 처리한 총 토큰 수)
구현 단순이론적 근거, 긴 문맥 안정짧은·긴 구간 모두 대응 가능
(zero fine-tuning 가능)
긴 컨텍스트에서 성능 붕괴짧은 구간 성능 손해
(trade-off 필요)		구현 복잡, 이론적 분석 부족
α 스케줄 설계 필요

Problem Definition

이러한 방식들을 “blind interpolation” method라고 정의한다. 위한 방법을 제안한다.

5) CoPE

3. 기타

이외에도 볼만한 논문들

1) Complex Embedding

2) Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains

3) Linear Positional Interpolation

4) Randomized PE

5) CAPE

4. Survey

Length Extrapolation of Transformers: A Survey from the Perspective of Positional Encoding

2024년 survey

1) Scaling Laws of RoPE-based Extrapolation

  • Dynamic NTK

2) Round and Round We Go! What makes Rotary Positional Encodings useful?

Artificial Intelligence, Research
research pe positional encoding transformer
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.