3. Modern Ciphers

샤논(Claude Shannon)에 따르면 안전한 블록 암호를 설계하기 위해 갖춰야 할 두가지 성질이 있다.

• Confusion(혼돈)
  

  Key-Ciphertext 사이의 관계를 감추는 성질
  

  AES/DES에서 혼돈 성질을 만족하기 위해 사용되는 요소는 치환(Substitution)이다.
  (e.g. S-box)

• Diffusion(확산)
  

  Plaintext-Ciphertext 사이의 관계를 감추는 성질

  마찬가지로 확산 성질을 만족하기 위해 주로 사용되는 요소는 전치(Transposition)이다. (e.g. P-box)

이러한 암호를 곱 암호(Product Cipher)라고 한다.

※ Substitution: 값 바꾸기, Transposition: 위치 바꾸기\

Block Ciphers

평문을 고정된 크기의 블록단위로 나누고 각 블록은 같은 키를 사용해 encryption하는 암호체계를 말한다. 한 번의 변환으로는 충분히 복잡하지 않기 때문에 여러 round를 반복하여 보안을 강화한다. 이 때문에 이 round를 정하는 것도 암호 체계에서 매우 중요한 issue이다.

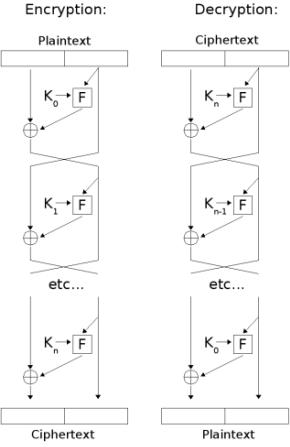
이 Block Cipher는 주로 Feistel Structure 라는 형태를 가지고 구현된다.

• 모든 round가 동일한 작업을 수행
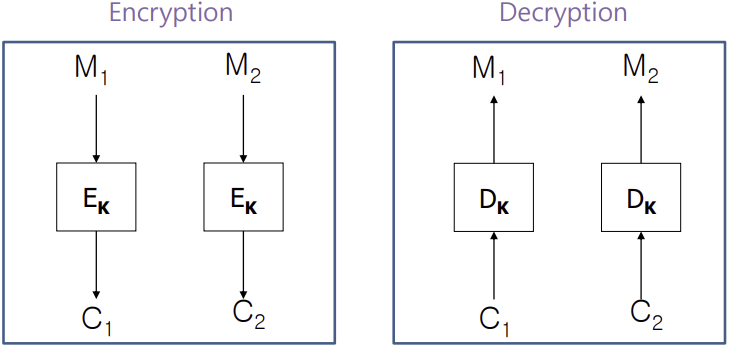
• Encryption 과정과 Decryption 과정이 거의 동일하다.

Symmetric Function

	Symmetric	Asymmetric
Encryption Key	Secret	Publlic
Decryption Key	Secret	Secret
Examples	DES, AES, SEED, ARIA	RSA, ElGamal
Key distribution	필수	불필요
Key 개수	많음	1개
속도	빠름	느림
전자 서명	불가능	가능

이번에는 암호의 특징에 따라 Symmetric Cipher와 Asymmetric Cipher로 나눌 수 있다. Symmetric Cipher의 경우 통신에 참여하는 모두가 상대와 자신의 Key를 소유하고 있어야 한다. 반면에 Asymmetric Cipher의 경우 Private Key를 가지고 있는 사람이 암호화 혹은 복호화만 진행하고 Public Key를 가지고 있는 사람이 이와 반대되는 함수만 사용한다.

1. Symmetric Key Ciphers

1) AES

DES

AES가 나오기 전에는 DES 알고리즘을 사용하였다. 하지만 DES Challenge라는 대회에서 DES Cracker라는 해독 알고리즘이 제안되었고, 더이상 안전하지 않은 알고리즘이 되었다.

---

Rijndael 알고리즘

1) Round 수 결정

우선 Feistel 구조에서 몇 Round를 사용할 지를 다음 표를 활용해 결정한다.

• Nr: Number of rounds
• Nb: Length of plaintext
• Nk: Length of key

Nr	Nb = 128 bits	Nb = 192 bits	Nb = 256 bits
Nk = 128 bits	10	12	14
Nk = 192 bits	12	12	14
Nk = 256 bits	14	14	14

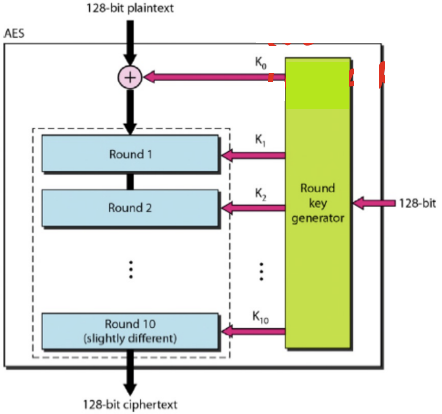
2) XOR with RoundKey

Key와 XOR 연산을 수행한다.

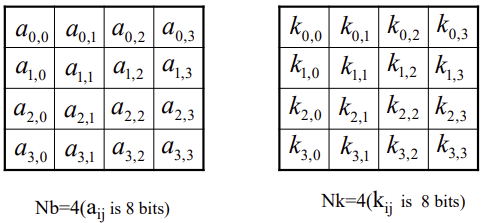
3) 평문/Key 변형

그 다음 평문과 Key를 다음과 같은 형태로 변형한다.

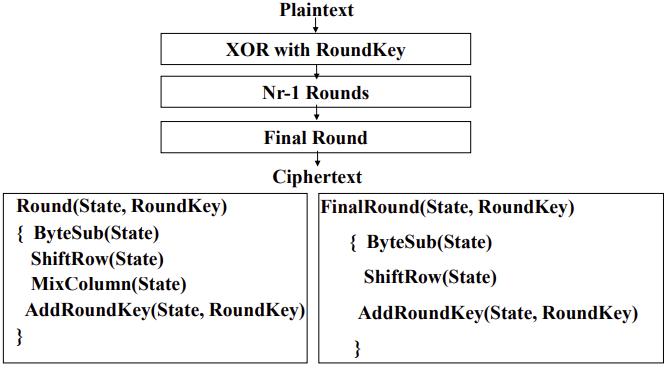
4) N-Round

다음 4가지 함수 반복 실행

• ByteSub(): S-box를 활용해 Byte 별로 값 교체
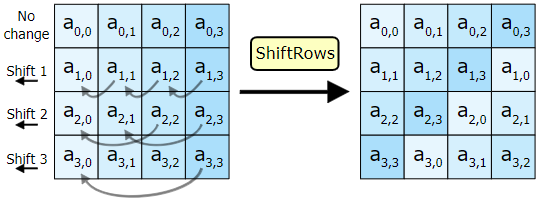
• ShiftRow(): i번째 행의 각 열을 i번 오른쪽으로 이동 (row by row)
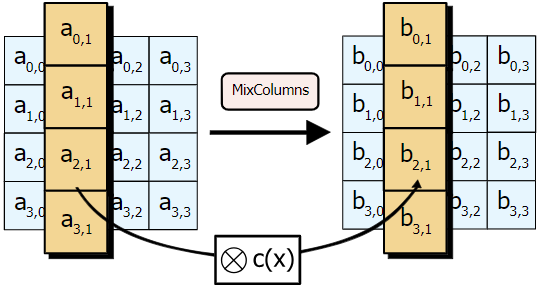
• MixColumn(): j번째 열에 특정 행렬을 행렬곱하여 새로운 열 생성 (column by column)
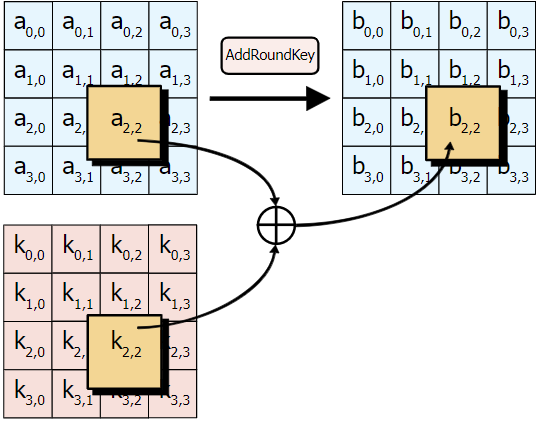
• AddRoundKey(): Byte별로 Key와 XOR연산을 통해 새로운 Ciphertext 생성 (Byte by Byte)

Shift Row	Mix Column	Add RoundKey

---

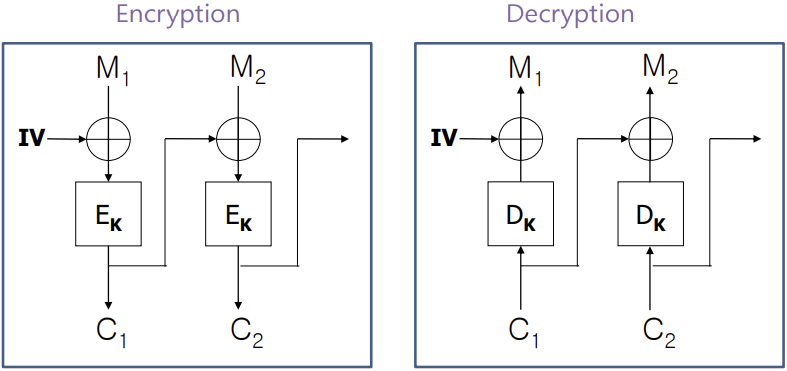
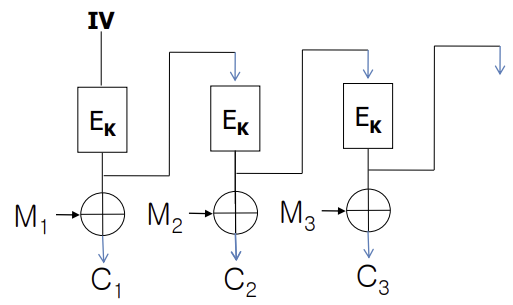
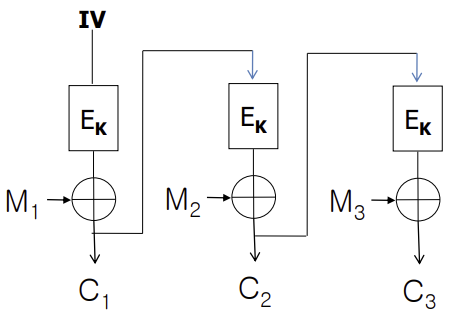
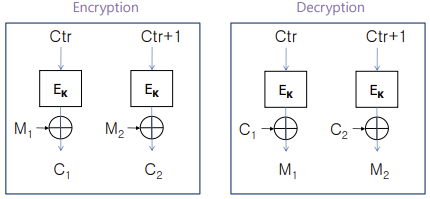
Mode

위의 알고리즘은 Plaintext와 Key의 길이를 결정하고 진행한다. 만약 암호화 하는 데이터의 크기가 미리 결정한 값보다 큰 경우 다음의 Mode를 사용해서 Block단위로 암호화한다.

각 모드별로 암호화된 문장을 Decryption할 때, 오류가 전파되는 정도가 달라진다.

	ECB Mode	CBC Mode
그림
설명	Block별로 순차적으로 암호화	순차적으로 암호화
장점	병렬 (ENC, DEC) 가능	병렬 DEC 가능 보안성이 가장 높음
단점	블록의 순서가 바뀔 경우 → 해독된 평문의 순서도 바뀜 $\quad$(이를 활용한 공격 가능)	다음 Block까지 오류가 전파됨 병렬 암호화가 어려움
오류 전파	1bit Error ($C_1$ ) → 1block Error($M_1$)	1bit Error ($C_1$) → 1block Error($M_1$) → 1bit Error($M_2$)

	OFB Mode	CFB Mode
그림
설명	KeyStream과 평문을 XOR 연산	Key Stream 생성 과정을 순차적으로 수행
장점	병렬 (ENC, DEC) 가능 ※ Key 스트림은 평문과 상관없이 오직 키와 IV로만 결정됨 → 미리 생성시 병렬 처리 가능	병렬 DEC 가능
단점	IV를 재사용시 취약해짐	다음 Block까지 오류가 전파됨 병렬 암호화가 어려움
오류 전파	1bit Error($C_1$) → 1bit Error($M_1$)	1bit Error($C_1$) → 1bit Error($M_1$) → 1block Error($M_2$)

	CTR Mode
그림
설명	블록을 암호화할 때마다 1씩 증가해 가는 카운터를 KeyStream으로 만들어 XOR 연산 (OFB와 같은 Stream 암호)
장점	병렬 (ENC, DEC) 가능
단점	Ctr 재사용시 취약해짐 블록의 순서가 바뀔 경우 → 해독된 평문의 순서도 바뀜 $\quad$(이를 활용한 공격 가능)
오류 전파	1bit Error ($C_1$ ) → 1bit Error($M_1$)

---

2. Hash Function & MAC

Cryptographic Hash Function의 종류는 다음 두가지와 같다.

1) Hash Function

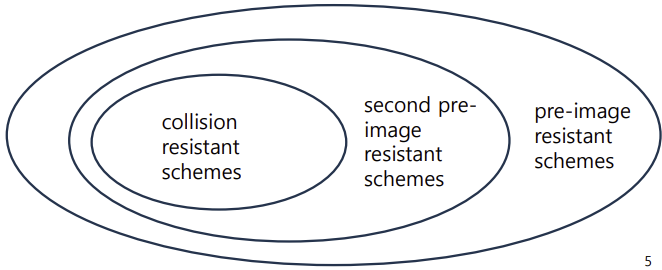
[해시 함수의 집합이 차지하는 공간]

암호학에서 해쉬함수는 다음의 3가지 특성을 가질 수 있다.

• Pre-image Resistance
  

  해시 값($h$)이 주어졌을 때, 해당 값을 만드는 입력($m$)을 찾기 어려워야 함.
  (One-way function의 속성을 가지고 있어야 함.)

• Second Pre-image Resistance
  

  입력 값($m$)이 주여졌을 때, 해당 입력의 해시값과 동일한 해시값을 갖는 입력($m’$)을 찾기 어려워야 함.

• Collision Resistance
  

  서로 다른 두 입력 값($m, m’$)이 동일한 해시값을 갖는 경우를 찾기 어려워야 함

※ 아래로 갈수록 더 강력한 요구 조건임.
※ 어떤 하나의 hash 값에 대한 pre-image는 $\infty$개가 존재한다.

---

Relationship

Collision Resistance를 만족하면 항상 Second Pre-image Resistance를 만족한다.
하지만, Pre-image Resistance는 만족하지 않을 수 있다.

이는 다음 두가지 상황으로 나누어 생각해볼 수 있다.

1. Sufficient Compression
   

   Hash 함수가 충분한 압축을 만족할 경우 $CR \in 2^\text{nd} PR \in PR$ 관계를 갖는다.
   ※ 충분한 압축이란? 입력 공간의 크기($\vert X \vert$)와 출력 공간의 크기($vert Y \vert$)가 $\vert Y \vert \ll \vert X \vert$를 만족해야 한다는 것을 의미한다.

2. Not Sufficient Compression
   

   반대로 충분한 압축이 없을 경우 $CR \in 2-PR \notin PR$ 관계를 갖는다.

대표적으로, 다음과 같은 해시함수가 있다고 생각해보자
\(H(x) = \begin{cases} 0 \Vert x & \text{if } \vert x \vert = n\text{ bit} \\ 1 \Vert g(x) & \text{otherwise}& \end{cases}\)

※ $g(x)$ 는 collision resistanct hash function

이 경우 ⅰ) 같은 Hash 값을 갖는 메시지는 존재할 수 없기 때문에 Collision Resistant를 만족한다.
ⅱ) 동일한 해시값을 갖는 입력이 없으므로 Second Pre-image Resistance도 만족한다
ⅲ) 하지만, 0으로 시작하는 (n+1) bit의 해시값이 주어진다면, 원래 입력($m$)을 Trivial하게, 쉽게 찾을 수 있으므로 Pre-image Resistance 조건은 만족하지 못한다.

비슷하게 $H(m) = m_1 \oplus m_2 \oplus … \oplus m_n, \quad (m = m_1 \Vert … \Vert m_n, \;\; \vert m_k \vert = 160 \text{ bit})$ 라고 정의된 함수도, 단순히 입력값이 160 bit만 들어온다고 하면 $H(m) = m$이므로 Pre-image Resistance를 만족하지 못한다.

2) MDC(Modification Detection Code)

\[m \Vert H(m)\]

• 목적: 데이터의 무결성(데이터가 변경되지 않음)을 확인하기 위해 사용한다.
• 특징: MDC를 위한 Hash 함수는 Key 없이 사용한다.
• 방법: 수신자가 앞부분을 Hash해서 뒷부분과 같은지 확인하여 메시지가 변경되었는지 확인한다.

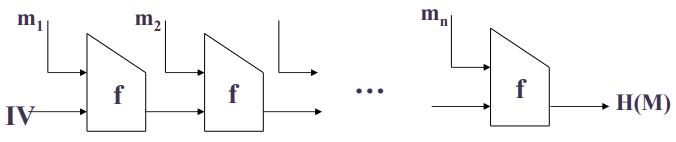
위의 조건들을 만족하는, Pre-image / 2nd Pre-image / Collision Resistance를 갖는 해시함수를 위해 MDC에서 주로 사용하는 함수의 형태는 다음과 같다.

$m = m_1 \Vert m_2 \Vert … \Vert m_n$

3) MAC(Message Authentication Code)

\[m \Vert MAC_k(m)\]

• 목적: 데이터의 무결성(데이터가 변경되지 않음)과 Sender를 함께 확인하기 위해 사용한다.
• 특징: MAC를 위한 Hash 함수는 Sender와 Receiver가 대칭 키를 가지고 있어야 한다.
• 방법: Sender가 Key를 사용해 Hash함수를 만들면 Receiver는 자신의 Key를 사용해 MAC을 복호화 함으로써 신뢰 가능한 주체가 메시지를 보냈음을 확인할 수 있다.

MDC를 사용하면 메시지 변경 여부를 확인할 수 있지만, 만약 공격자가 중간에 메시지를 가로채서 MDC까지 함께 바꾸어 전송한다면 알 수 있는 방법이 없다.
$\text{Sender} \rightarrow m \Vert H(m) \rightarrow \text{Adversary} \rightarrow m’\Vert H(m’) \rightarrow \text{Receiver}$

필요 조건: Strong unforgeability

어떠한 공격자도 (유효한 메시지, 시그니처) 쌍을 생성할 수 없다.

---

Forgery Game

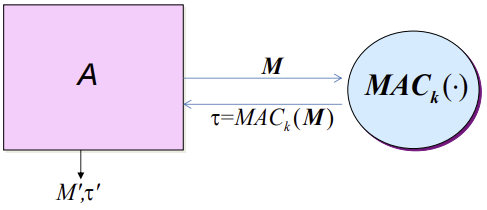
안전한 MAC을 구성하기 위해서는 Adversary가 Forgery Game에서 이기기 힘든 함수를 만들어야 한다.

Adversary 조건

• Mac Oracle을 가지고 있음 (private key를 제외한 알고리즘을 알고있음)
• 최종적으로 선택한 Message($M’$)를 Mac Oracle을 사용하지 않고 $\tau’$로 만들어야 함.

$\rightarrow MAC_k (M’) = \tau’$일 경우 공격 성공

위의 Forgery Game에서 안전하지 않은 대표적인 예시를 살펴보면,

\[m = m_1 \Vert m_2 \Vert ... \Vert m_n \\ MAC_k(m) = E_k(m_1 \oplus m_2 \oplus ... m_n) \\\]

Adversary가 $m_1$과 그에 대한 MAC인 $\tau_1 = MAC_k(m_!)$을 MAC Oracle을 통해 알아냈다고 하자.
이때, Adversary가 $m_2 = m_1 \Vert 0…0$ 이라고 정의하면, 바로 $\tau_2 = MAC_k(m_2) = \tau_1$ 이라는 것을 알아낼 수 있다.

※ Kerckhoffs’s Principle: 암호 시스템의 안전성은 비밀키에만 의존해야 하고, 알고리즘 구조는 공격자에게 알려져 있다고 가정해야 한다.

---

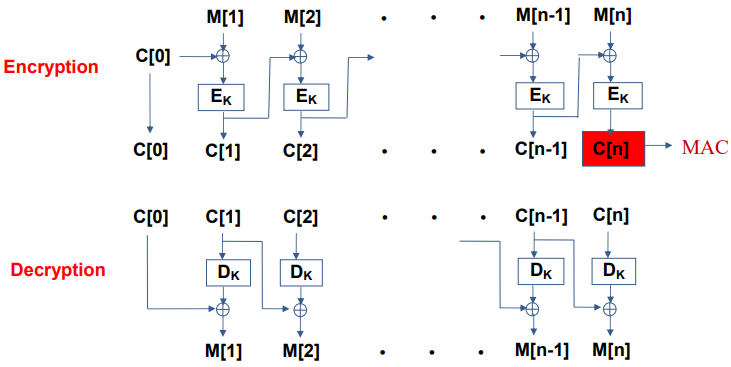
CBC MAC

MDC와 마찬가지로 위의 Forgery Game에서 안전한 형태의 MAC으로 주로 사용하는 형태가 있다.
다음과 같이 CBC 형태로 평문을 암호화 한 후에 마지막에 나온 값을 MAC으로 사용하는 방법이다.

---

HMAC

공유키와 MDC Hash function으로 MAC의 역할을 하는 함수를 만들수도 있다.

$MAC_k(m) = H(k \Vert m)$으로 설정하면 $m \Vert H(k \Vert m)$이 되기 때문에 Receiver는 자신의 key와 함께 message를 hash해 보는 방식으로 인증 작업을 거칠 수 있다.

---

3. Asymmetric Key Ciphers

비대칭 키를 사용한 암호 체계에는 대표적으로 Public-Private Key 구조를 사용하는 방식이 있다.

AES등 Symmetric Encryption의 경우 매우 암호화/복호화 속도가 매우 빠르고, 키의 길이가 짧다는 장점이 있지만 다음과 같은 단점이 존재한다.

• Key distribution problems: 임의의 다른 사람들과 비밀리에 소통하는 것이 불가능하다.
• Key management problems: Key의 개수가 통신에 참여하는 사람들의 수에 따라 달라진다.

※ 이외에도 전자 서명이 불가능하기 때문에 부인 방지가 불가능하다는 문제가 있다.

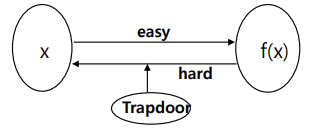
이 때문에 속도와 Key 길이에 대한 장점을 포기하고 Symmetric Encryption의 단점을 보완하는 다음과 같은 One-way function에 대한 필요가 발생하였다.

즉, 공개키 시스템에서는 $f^{-1}$을 구하는 것이 얼나 어려운지에 따라 이 암호의 Security가 결정된다.

1) RSA

1) 원리

정수론에 기반해 매우 큰 수의 소인수 분해 문제를 이용하는 방식이다. 하드웨어 성능이 발전함에 따라서 RSA는 사용하는 비트 수를 늘려가며 계산을 복잡하게 만드는 방식으로 지금까지 쓰이고 있고, 현재는 Key로 최소 2048 bit를 사용하고 있다.

Euler’s Theorem

만약 $\gcd(a, n) = 1$(n과 a가 서로소)이면,
$a^{\Phi(n)} \equiv 1 (\bmod n)$ 이다.

※ $\Phi(n)$는 n과 서로소인 숫자들의 수

---

2) Key 생성

ⅰ. 소수 2개를 선택한다
$\quad$ (e.g. p=2, q=7)

ⅱ. 공개키 $n = p \times q$를 구한다
$\quad$ (e.g. n = 14)

ⅲ. $\Phi(n) = (p-1)(q-1)$을 구한다.
$\quad$ (e.g. $\Phi(n) = 6$)

ⅳ. $n$과 서로소이면서 $1 < e < \Phi(n)$인 공개키(e)를 선택한다.
$\quad$ (e.g. $e = 5$ 선택)

ⅴ. $d \times e \times mod \, \Phi(n) = 1$ 인 비밀키(d) 를 선택한다.
$\quad$ (e.g. $d = 5$ 선택)

---

3) 암호화/복호화

• 암호화
  $c = m^e \bmod n$

• 복호화
  $m = c^d \bmod n$

※ CRT (Chinese Remainder Theorem)를 사용하면 더 빠르게 복호화가 가능하다. v

복호화 증명

1. 우선 암호문은 다음과 같다.
   \(c^d \, \bmod n \equiv m^{ed} (\bmod pq)\)

2. 즉, $m^{ed} \equiv m \, (\bmod p), \quad m^{ed} \equiv m \, (\bmod q)$ 임을 증명하면,
   $m^{ed} \equiv m \, (\bmod pq)$ 을 증명할 수 있다.

3. $m^{ed} \equiv m \, (\bmod p)$ 임을 먼저 증명해보자.
   $p$가 소수이기 때문에 $\gcd(m, p)$는 다음 두가지 경우로만 나누어진다.

① $gcd(m, p) = 1 \rightarrow m^{\Phi(p)} \equiv 1 \, (\text{mod }p)$	② $gcd(m, p) = p \rightarrow m = kp$
\(m^{ed} = m^{1 + k\Phi(n)} = m^{1 + k(p-1)(q-1)} \\ = m \cdot (m^{\Phi(p)})^{k(q-1)} \\ \equiv m \cdot 1^{k(q-1)} \, (\bmod p) \\ \equiv m \, (\bmod p)\)	\(m^{ed} \\ = (kp)^{ed} \\ \equiv 0 \, (\bmod p) \\ \equiv m \, (\bmod p)\)

※ $m^{ed} \equiv m \, (\bmod q)$ 또한 같은 방식으로 증명 가능하다.

---

4) 취약점

• Factorization Attack: 인수분해 공격
  

  n을 빠르게 인수분해 하는 알고리즘을 사용하면 공격 성공
  → 충분히 긴 키를 사용해야 함

• CCA(Chosen Ciphertext Attack)
  

  공격자가 Decryption oracle의 상황일 경우 임의의 공개키 $r$을 이용해 복호화 가능
  → OAEP와 같은 패딩 기법을 사용해야 함

• Small e + Same small message + Different n’s
  

  여러 수신자와 위 조건을 만족하며 통신하는 경우 CRT를 이용해 원문을 복원할 수 있음

• Circular Encryption Attack
  

  암호문과 평문은 1대 1 대응이다. 또한 Modular 연산을 사용하기 때문에, 암호화 연산을 반복하면 순환이 생김
  즉, 이를 따라가면 원문을 역추적 할 수 있음
  (e.g. $c=m^e \bmod n \;, c_1 = c^e \bmod n \;, … c_k - c_{k-1}^e \bmod n = c$ 인 경우)

※ CCA 예시

ⅰ. 주어진 암호문
$c = m^e \bmod n$

ⅱ. 공격자는 $\gcd(r,n)=1$ 이면서 $r \in (0,n-1)$ 인 임의의 값 $r$을 선택
$r^{\Phi(n)} \equiv 1 \pmod n$

ⅲ. 공격자는 공개키 $e$를 이용해 다음과 같은 변형 암호문을 만듦
$c^\ast = r^e \cdot c \bmod{n}$

ⅳ. 공격자는 복호화 오라클에 $c^\ast$를 전송하고, 복호화 결과 $(c^\ast)^d \bmod n$를 받아옴
\(c^{\ast d} \bmod n \\ \equiv (r^e \cdot c)^d \pmod n \\ \equiv r^{ed} \cdot c^d \pmod n \\ \equiv r^{1+k\Phi(n)} \cdot c^d \pmod n \\ \equiv r \cdot r^{k\Phi(n)} \cdot c^d \pmod n \\ \equiv rm \pmod n \\\)

ⅴ. 즉, 복호화 오라클에서 받아온 값에 $\frac{1}{r}$을 곱하면 원문을 구할 수 있음

---

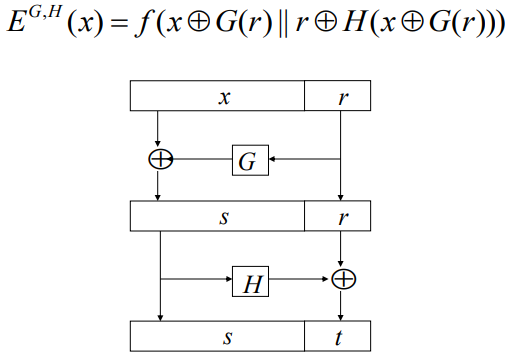
5) 방어기법(OAEP) v

기호	의미	설명
$x$	메시지 블록	평문에서 일부 잘라낸 블록
$r$	랜덤 시드(random seed)	매 암호화 시마다 새로 생성되는 난수
$G$	Mask Generation Function	입력된 시드 $r$로부터 $x$ 크기의 마스크를 생성
$H$	Hash Function	마찬가지로 입력된 마스크된 (x)에서 시드 크기의 마스크를 생성
$\oplus$	XOR 연산	비트 단위 XOR (마스킹/언마스킹에 사용됨)
$\parallel$	Concatenate (연결)	두 블록을 이어 붙이는 연산

2) Elgamal

이산 대수 문제를 이용하는 방식이다.

---

1) Key 생성

ⅰ. 매우 큰 소수 n 선택

ⅱ. $d \in [1, n-1], e_1 \in \mathbf{Z}_n^\ast$ 선택

ⅲ. $e_2 = e_1^d \bmod n$

• $\text{Public Key} = [e1, e2, n]$
• $\text{Private Key} = [d]$

---

2) 암호화/복호화

• 암호화
  

  $c = [c_1, c_2] = [e_1^k \bmod n, me_2^k \bmod n]$
  $\quad (k \in [1, n-2])$ 인 임의의 정수

• 복호화
  

  $m = c_2 c_1^{-d} \bmod n$

4. Digital Signature

MAC은 대칭키 시스템을 사용하기 때문에 Signature역할을 하지 못한다. 하지만 비대칭 키 시스템을 사용한다면 디지털 서명의 역할을 하는 메시지를 만들 수 있다.

• MAC: 비공개 환경에서 두 사람 사이에서만 유효한 서명
• Digital Signature: 공개 환경에서 누구에게나 증명 가능한 서명

생성 과정은 Private Key를 갖고 있는 사람이 sign을 하면 다른 사람이 Public Key를 가지고 복호화 하여 확인하는 방식이다.
(공개키 암호화 과정이랑 반대이다.)

1) RSA Signature

• Signing algorithm
  $s = H(m)^d \bmod n$

• Verification algorithm
  $s^e \equiv H(m)^e \pmod n$

※ Public Key: [e, n]
※ Private Key: [d, n]

Strong Unforgeability

이때, Hash 함수가 위에서 설명했던 3가지 특성을 만족하지 못하면 Strong Unforgeability를 만족하지 못한다.
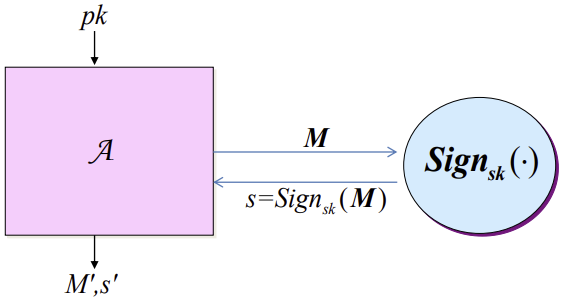
이를 살펴보기 위해 Digital Signature의 Security Model을 살펴보자.

여기서, 공격자의 조건은 다음과 같다

• 위조하고자 하는 대상의 Public Key를 알고 있다.
• 위조하고자 하는 대상의 Signing oracle을 가지고 있다.
  (최종 제출 메시지를 제외한 메시지에 대한 Signature를 알 수 있다.)
• 최종 제출한 $M’, S’$에 대해 Verify 알고리즘을 통과해야 한다.

만약 Hash 함수가 Second Pre-image Resistance를 만족하지 못한다고 하자. 그러면 공격자는 입력 $m$과 동일한 해시값을 갖는 입력 $m’$을 찾을 수 있다. 즉, 최종 제출시 $m’, s$를 내놓으면 Verify 알고리즘을 통과하여 Strong Unforgeability를 깰 수 있게 된다.

2) DSA Signature

• Signing algorithm
  ⅰ) $k \in [1, n-1]$이고, $\gcd(k, n-1) = 1$ (n-1과 서로소인 k)를 선택
  ⅱ) $r \equiv e_1^k \bmod n$ 계산
  ⅲ) $s = (h(m) - dr)k^{-1} \bmod (n - 1)$ 계산
  $\Rightarrow$ Signature = $(r, s)$

• Verifying algorithm
  

  $e_1^{h(m)} \equiv e_2^rr^s \bmod n$인지 확인

※ Elgamal을 이용한 Signature

3) 변형들

Blind Signature

E-cash, CBDC에서 사용

중앙 은행이 있는 구조

• 발행: 중앙은행의 서명이 있는 화폐 → 서명시 Custommer의 Account에서 1을 감소
• 확인: 중앙은행의 서명이 있는지 확인 → Shop의 Account에 1을 증가

1. 고객 준비 (Blinding)

   • 고객은 새 전자화폐의 식별자(serial number) (m)을 만듦
   • 그리고 블라인딩 계수 (r) 를 이용해 메시지를 가림
     \(m' = m \cdot r^e \pmod{n}\)
     (여기서 (e, n)은 중앙은행 공개키, (r)은 고객만 아는 무작위 수)

2. 중앙은행 서명 (Signing)

   • 중앙은행은 고객이 보낸 (m’)에 자신의 비밀키 (d) 로 서명
     \(s' = (m')^d \pmod{n}\)
   • 이때 중앙은행은 실제 (m)의 내용은 볼 수 없음(블라인드되어 있기 때문).

3. 고객의 언블라인드 (Unblinding)

   • 고객은 받은 (s’)에서 자신의 블라인딩 계수를 제거
     \(s = s' \cdot r^{-1} \pmod{n}\)
   • 그럼 최종적으로 ($s = m^d \pmod{n}$), 즉 정상적인 중앙은행의 서명된 전자화폐가 완성

4. 결과: 고객은 중앙은행으로부터 유효한 전자화폐(은행 서명 포함)를 받았지만,
   중앙은행은 누구에게 어떤 지폐를 서명해줬는지 알 수 없음.