포스트

7. Machine Learning

게시 업데이트
By UI-JIN KIM 13 분읽는 시간

Machine Learning

Machine Learning에는 크게 2가지 종류가 존재한다.

  1. Deductive Learning
    규칙들을 분석해 새로운 규칙을 찾아내는 것

  2. Inductive Learning
    데이터에 기반해 규칙을 찾아내는 것

    • Supervised Learning(지도학습)
      label(정답)이 있는 학습과정
      $\rightarrow$ Classification(분류), Regression(함수값 예측)
    • Self-Supervised Learning
      label(정답)을 임의로 만들어 Embedding(representation)을 학습하는 것
      (후에 학습 된 representation를 활용하여 모델이 좋은 성능을 가지게 할 수 있음)
      $\rightarrow$ Self-Prediction, Contrastive Learning
    • Unsupervised Learning(비지도 학습)
      label(정답)이 없는 학습과정
      $\rightarrow$ Clustering
    • Reinforcement Learning
      label(정답)이 없고 보상을 통해 행동을 학습하는 것

1. Hypotheses

1) Hypothesis

Machine Learning의 목표는 미래의 Data(Test Data)에 대해서 잘 작동하는 함수를 찾는 것이다. 이를 위해서 다음과 같은 개념이 도입된다.

  • Target Function
    Input에 대해 우리의 Task에 알맞은 Output을 내는 목표함수
    (즉, Target Function은 “Unknown”이다.)
  • Hypothesis Function
    Train Data를 관찰한 결과 Target Function일 것이라고 가정한 함수
  • Generalization
    Train에서 학습한 모델이 Test Data에서도 잘 동작하도록 하는 것

즉, 우리의 목표는 Generalization이 잘 된 Hypothesis Function을 찾는 것이다.

Bias & Variance

alt text

  • Bias
    Hypothesis Space와 실제 Target Function과의 거리를 의미한다.
  • Variance
    Hypothesis Space의 범위를 의미한다.
    범위가 너무 크면 Target Function뿐만 아니라 다른 Noise들도 배우기 때문에 문제가 발생한다.

Error는 Bias와 Variance의 합으로 표현할 수 있다.

2) Hypothesis Spaces

가능한 모든 Hypothesis Function이 속한 공간을 의미한다.

즉, 이 Hypothesis Space에서 Target Function과 가장 유사한 Hypothesis Function을 찾아야 한다.

주의점

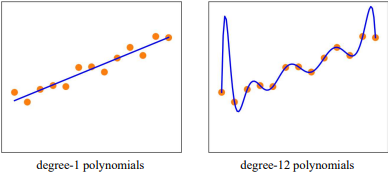
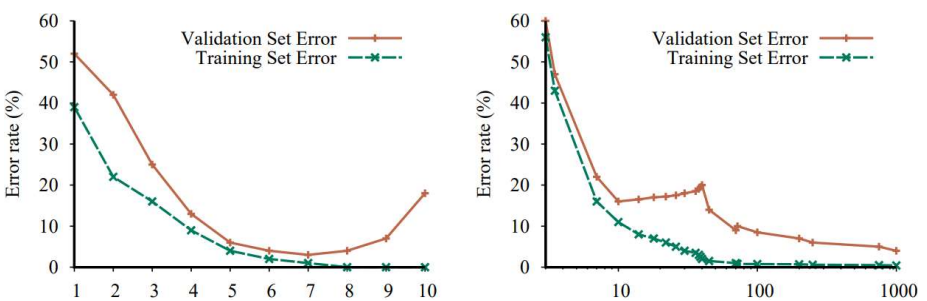
  • Under Fitting
    train data으로 학습할 때, Target Function을 찾지 못해 발생하는 상황이다.
    $\rightarrow \quad \because$ Bias
  • Over Fitting
    Target Function은 찾았지만 Generalization이 되지 않은 상황이다.
    $\rightarrow \quad \because$ Variance

이러한 Under Fitting과 Over Fitting현상을 막기위해서는 적절한 Complexity를 갖는 Model을 사용하는 것이 중요하다.

※ Ockham’s Razor
$\quad$ Ockham’s Razor는 필요 이상의 복잡한 가설(모델)을 사용하지 말자는 일종의 철학을 말한다.

Probable Hypothesis

그럼 이제 이 Hypothesis Space에서, 어떻게 Best Hypothesis Function을 찾을 수 있을까?
이 문제를 풀기 위해 Bayes’ Rule을 적용해보자

우리는 데이터가 주어졌고 가설 h가 있을 때, h는 간단하게 정의되어 있을 확률이 높으므로 h가 작을 때 $P(h)$는 커진다고 정의하자.

$h^* = \text{arg}\max \limits_{h \in \mathcal{H}} P(h | data)$
$\quad\; = \text{arg}\max \limits_{h \in \mathcal{H}} \frac{P(data | h)P(h)}{P(data)}$
$\quad\; = \text{arg}\max \limits_{h \in \mathcal{H}} P(data | h)P(h)$

즉, 최적의 가설 $h^*$는 데이터를 잘 설명하면서, 가장 간단한 가설이 된다.

2. Model

1) Loss Function

Error Rate

예측값과 정답이 다른 비율을 의미한다.

$E(h) = \frac{1}{N} \sum \limits_{i=1}^N [[h(x) \neq y]]$

Loss Function

Loss Function이란 최적의 상황에서의 Utility랑 현재 상황에서 Uitlity의 차이를 의미한다.
$L(x, y, \hat{y}) = Utility(x, y) - Utility(x, \hat{y})$

참고로 이때, $L(a, b) \neq L(b, a)$임을 주의하자.

ⅰ. 0/1 Loss
\(\qquad L_{0/1}(y, \hat{y}) = \begin{cases} 0, \quad (y=\hat{y}) \\ 1, \quad (otherwise) \end{cases}\)

ⅱ. Absolute-Value Loss
\(\qquad L_1(y, \hat{y}) = \vert y-\hat{y} \vert\)

ⅰ. Squared-Error Loss
\(\qquad L_2(y, \hat{y}) = (y-\hat{y})^2\)

Generalization Loss

위의 Loss Function을 정의하고 난 후, 우리는 Utility의 기댓값인 Generalization Loss를 정의할 수 있다.

\[\text{GenLoss}_L(h) = \sum \limits_{(x, y) \in \epsilon} P(x, y)L(y, h(x))\]

이때, $P(x, y)$를 알 수 없으므로 이를 $\frac{1}{N}$으로 두고 계산하기도 한다.
즉, 인공지능은 다음의 식을 풀게 된다.

\[h^* = \text{arg}\min \limits_{h \in \mathcal{H}} \text{EmpLoss}_L(h) = \text{arg}\min \limits_{h \in \mathcal{H}} \frac{1}{N} \sum \limits_{(x, y) \in \epsilon} L(y, h(x))\]

※ 우리는 Data가 iid(independent identically distributed)라고 가정한다.
\(\quad P(E_j) = P(E_j \| E_{j-1}, E_{j-2}, ...) \\ \quad P(E_j) = P(E_{j+1}) = P(E_{j+2})\)

2) Model Selection

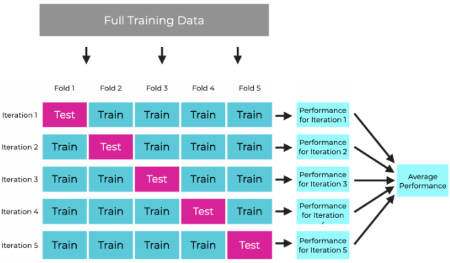
alt text

Cross-Validation

alt text

Train과 Validation을 동시에 하면서, Validation error가 가장 작을 때의 모델을 고르는 것

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def model_selection(learner, examples, k):
  err = []
  train, test = examples.split()
  for size in range(1, 1e9):
      err[size] = cross_validation(learner, size, train, k)
      if err[size] > err[size-1]:
          best = min(err[:size-1])
          h = learner(best, train)
          return h, error_rate(h, test)

def cross_validation(learner, size, examples, k):
  N = len(examples) 
  err = 0
  for i in range(k):
      valid = examples[(i-1)*N/k : i*N/k]
      train = examples - valid
      h = learner(size, train)
      err = err + error_rate(h, valid)
  return err / k

※ LOOCV(Leave-One-Out Cross Validation): Validation은 Sample 1개로만 하는 것

Hyperparameter Tuning

1. Hand-Tuning직관을 사용해 조정
　
2. Grid Search몇몇 Hyperparameter들에 대해 가능한 값들을 설정하고
이 값들의 모든 조합에 대해 최적의 값을 찾는 방식
ex. param_grid = {'n_estimators': [100, 150, 200],
$\qquad\qquad\quad\qquad$ 'max_depth' = [None, 6, 9, 12], }
　
3. Random Searchrandom하게 Hyperparameter들을 정해 최적의 값을 찾는 방식
　
4. Bayesian Optimizationvalidation data에서 각 Hyperparameter에 대한 성능을 평가하고
이를 통해 Hyperparamter($x$)와 성능($y$)간의 함수 $y=f(x)$를 추정하는 방식
　
5. Population-based Trainingⅰ. Sequential Search: Bayesian Optimization
ⅱ. Parallel Search: Random Search
두 종류의 방법은 장단점이 있으므로 두 방법을 연결하여 사용해보자
　

3) Regularization

alt text

Noise

실제 우리가 구한 가설($\hat{h}^*$)과 실제 결과인 target function($f$)가 차이나는 이유는 다음과 같다.

  • Training Data의 Variance
  • f에 존재하는 Noise까지 학습
  • H의 Complexity의 한계로 인한 구현 불가($f \notin \mathcal{H} $)

이 문제를 해결하기 위해 Regularization이 필요하다.

Regularization

Regularization은 가설공간 $\mathcal{H}$에 추가적인 제약을 걸어 Variance를 줄여주는 역할을 한다.

\[\mathbf{w}^* = \text{arg} \min \limits_\mathbf{w} (\text{Loss}(h_\mathbf{w}) + \lambda \text{Complexity}(h_\mathbf{w})\]
  • Complexity
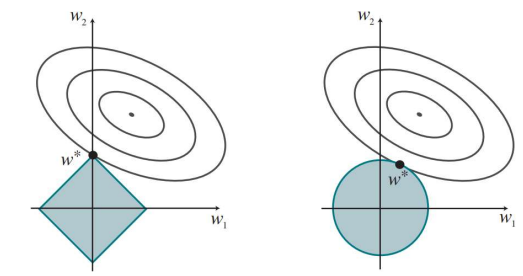
    • L1 Regularization: $\text{Complexity}(h_\mathbf{w}) = \sum \limits_i \vert w_i \vert$
    • L2 Regularization: $\text{Complexity}(h_\mathbf{w}) = \sum \limits_i w_i^2$
    • $\lambda \propto$ Regularization 정도

※ 만약 Complexity를 L1-Norm으로 한다면 Feature Selection 효과를 얻을 수 있다.

Linear Model

1. Regression

1) Linear Regression

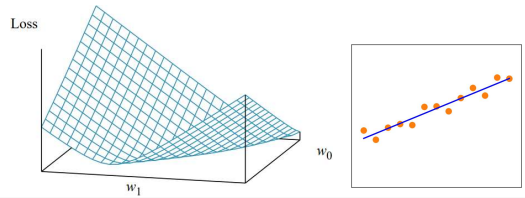
alt text

Univariate Linear Regression

\[h_\mathbf{w}(x) = w_1x + w_0\]

Loss함수를 L2-Norm으로 정했을 때, 이 함수는 Convex함수이므로 미분값이 0이 되는 지점에서 최소값을 갖는다.

\(\text{Loss}(h_\mathbf{w}) = \frac{1}{N} \sum \limits_{(x, y)} L_2(y, h_\mathbf{w}(x)) = \frac{1}{N} \sum \limits_{(x, y)}(y-h_\mathbf{w}(x))^2 \\ \\ \nabla_\mathbf{w_0} = -2 \sum \limits_{(x, y)}(y-h_\mathbf{w}(x))\nabla_{w_0}h_\mathbf{w}(x) = 0\\ \nabla_\mathbf{w_1} = -2 \sum \limits_{(x, y)}(y-h_\mathbf{w}(x))\nabla_{w_1}h_\mathbf{w}(x) = 0\\\)
$\therefore w_1 = \frac{N\sum \limits_{(x, y)}xy - (\sum \limits_x x)(\sum \limits_y y)}{N \sum \limits_x x^2 - (\sum \limits_x x)^2}\qquad w_0 = \frac{\sum \limits_y y - w_1 \sum \limits_x x}{N}$

Multivariable Linear Regression

\[h_\mathbf{w}(x) = \mathbf{w} \cdot \mathbf{x} \qquad (\mathbf{w} = \begin{bmatrix}w_0 \\ \vdots \\ w_n\end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix}x_0=1 \\ \vdots \\ x_n\end{bmatrix})\]

Univariate와 마찬가지로 미분값이 0이되는 부분을 찾아보자

\(\text{Loss}(h_\mathbf{w}) = \frac{1}{N} \sum \limits_{(\mathbf{x}, y)} L_2(y, h_\mathbf{w}(\mathbf{x})) = \frac{1}{N} \sum \limits_{(\mathbf{x}, y)}(y-\mathbf{w}^T\mathbf{x})^2 = \frac{1}{N} \Vert \mathbf{y} - W^T X \Vert^2\\ \qquad \qquad = \frac{1}{N}(\mathbf{y} - W^TX)^T(\mathbf{y} - W^TX) \\ \qquad \qquad = \frac{1}{N}(\mathbf{y}^T\mathbf{y} -2W^TX^T\mathbf{y} + W^TX^TXW) \\ \nabla_\mathbf{w}\text{Loss}(h_\mathbf{w}) = \nabla_\mathbf{w} \frac{1}{N} \Vert \mathbf{y} - W^T X \Vert^2 \\ \qquad \qquad \quad \; = \frac{1}{N}(- 2X^T\mathbf{y} + 2X^TXW) = 0\\ \rightarrow X^T\mathbf{y} = X^TXW\)
$\therefore W = (X^TX)^{-1}X^T\mathbf{y}$

2) Gradient Descent

alt text

위의 Linear Regression에서 Loss를 구하는 과정을 보면, (1024 $\times$ 1024) Image만 생각하더라도 엄청난 양의 연산량이 필요하다는 것을 알 수 있다.
이렇게 Input $X$의 크기가 커지면 한번에 최적점을 구하는 것이 아닌 Iterative하게 구하는 방법이 필요하다.

\[\nabla_\mathbf{w}\text{Loss}(h_\mathbf{w})=0 \qquad \rightarrow \qquad W = W - \alpha \nabla_\mathbf{w}\text{Loss}(h_\mathbf{w})\]

즉, 다음과 같은 알고리즘을 설계해볼 수 있다.

1
2

for i in range(N):
    w[i] = w[i] + lr * sum(y - w@x) * x[i]

Stochastic Gradient Descent

또, 단 하나의 Sample을 Random하게 골라 loss를 확인하는 방법이 있다.
$\rightarrow$ each $(\mathbf{x}, y) \in \mathcal{D}$ in random
이렇게 기다리지 않고 데이터에 대해 바로 학습하기 때문에 Online Gradient Descent라고도 불린다.

1
2
3

j = randint(N)
for i in range(N):
    w[i] = w[i] + lr * (y[j] - w@x[j]) * x[i]

장점

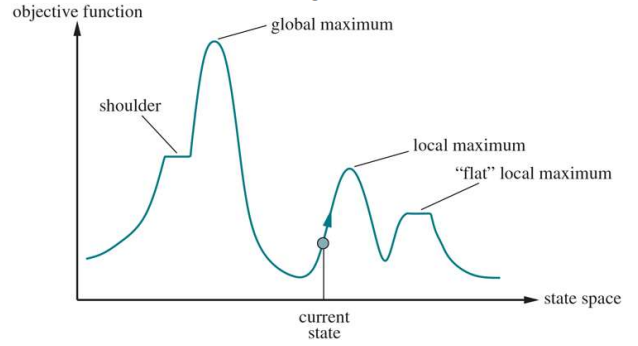
  • Non Convex한 Object Function을 갖고있을 경우 Batch Gradient Descent는 Local Minimum을 빠져나올 수 없다
    $\rightarrow$ SGD는 전체가 아닌 하나의 Sample에 대해서만 Loss를 구하기 때문에 빠져 나올 기회를 줄 수 있다.

단점

  • Global Minimum 또한 빠져나올 수 있다.
    $\rightarrow$ 시간에 따라 Learning Rate를 조절하여 수렴하게 만든다.

Mini-Batch Stochastic Gradient Descent

몇개의 Sample을 Random하게 골라 loss의 평균을 확인하는 방법
$\rightarrow$ each $(\mathbf{x}, y) \in \mathcal{D}^{batch_size}$ in random
즉, Stochastic Gradient Descent + Batch Gradient Descent인 것이다.

장점

  • 빠른 시간안에 수행할 수 있다.
    (GPU의 parallel processing이 가능하다.)

Batch의 Size를 키울수록 수행 시간이 빨라지고 Batch Size = Data Size일 경우 Batch Gardient Descent와 같아진다.

즉, Batch의 크기를 키울수록, Local Minimum에 빠질 확률이 늘어난다.

2. Classification

1) Linear Classification

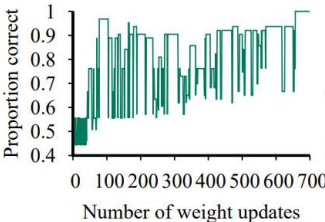
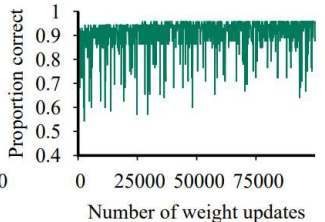
alt text

\[h_\mathbf{w}(\mathbf{x}) = \text{Threshold}(\mathbf{w} \cdot \mathbf{x}) = \begin{cases} 1, \qquad (\mathbf{w}^T\mathbf{x} > 0)\\ 0 \qquad \text{otherwise}\end{cases}\]

PLA (Perceptron Learning Algorithm)

1
2
3
4

h = max(weight=w, threshold=0)
j = randint(N)
for i in range(N):
    w[i] = w[i] + lr * (y[j] - h(x[j])) * x[i]
Linearly SeperableLinearly UnseperableLinearly Unseperable
alt textalt textalt text
PLA를 사용하면
정답률이 1로 수렴한다.		PLA를 사용해도
정답률이 1이 되지 않는다.		Learning Rate를 점차 줄일 경우
Oscillation을 줄일 수 있다.

2) Logistic Regression

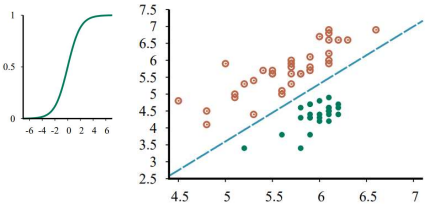
alt text

\[h_\mathbf{w}(\mathbf{x}) = \text{Logistic}(\mathbf{w} \cdot \mathbf{x}) = \frac{1}{1+e^{-\mathbf{w}^T\mathbf{x}}}\]

※ Logistic(Sigmoid) Function을 사용하는 이유
\(\quad g(z) = \frac{1}{1+e^{-z}} \quad \rightarrow \quad \nabla_z g(z) = g(z)(1-g(z))\)
$\quad$ 즉, 미분값을 쉽게 구할 수 있다.

Loss

\(\text{Loss}(h_\mathbf{w}) = L_2(y, h_\mathbf{w}(\mathbf{x})) = (y- h_\mathbf{w}(\mathbf{x}))^2\\ \\ \nabla_\mathbf{w_i}\text{Loss}(h_\mathbf{w}) = \nabla_\mathbf{w_i} (y - h_\mathbf{w}(\mathbf{x}))^2 \\ \qquad \qquad \quad \;\; = -2(y-h_\mathbf{w}(\mathbf{x})) \nabla_{\mathbf{w}_i} h_\mathbf{w}(\mathbf{x}) \\ \qquad \qquad \quad \;\; = -2(y-h_\mathbf{w}(x))h(\mathbf{x})(1-h_\mathbf{w}(\mathbf{x})) \nabla_{\mathbf{w}_i} (\mathbf{w} \cdot \mathbf{x}) \\ \qquad \qquad \quad \;\; = -2(y-h_\mathbf{w}(x))h(\mathbf{x})(1-h_\mathbf{w}(\mathbf{x})) x_i\)
$\therefore W = (X^TX)^{-1}X^T\mathbf{y}$

Learning

1
2
3
4

h = sigmoid(weight = w)
j = randint(N)
for i in range(N):
    w[i] = w[i] + lr * (y[j] - h(x)) * h(x) * (1-h(x)) * x[i]

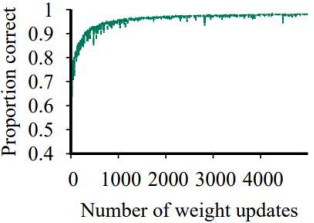
PLA에서 $h(x) * (1-h(x))$항만 추가된 것을 확인할 수 있다.
즉, Logistic Regression은 PLA의 Soft한 버전이다.

Linearly SeperableLinearly UnseperableLinearly Unseperable
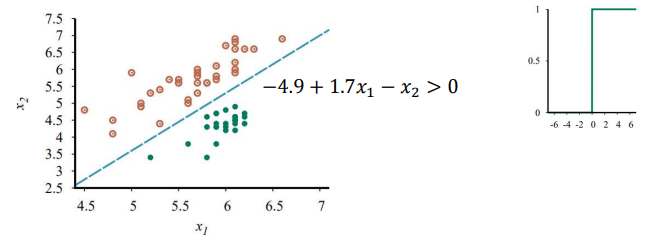
alt textalt textalt text
시간이 오래걸리지만
정답률이 1로 수렴한다.		정답률이 1이 되지 않지만
거의 수렴한다.		정답률이 1이 되지 않지만
더 빨리 더 가까이 수렴한다.
Artificial Intelligence, AI
ai linear regression linear classification
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.