4. KKT Condition
1. Duality
\[\text{minimize} \quad \quad \;\; f_0(\mathbf{x}) \\ \text{subject to} \quad f_i(\mathbf{x}) \leq 0, \\ \qquad \qquad \quad h_i(\mathbf{x}) = 0\]Standard Form Problem(=Primal Problem)
1) Lagrangian Function
\[L(\mathbf{x}, \lambda, \nu) = f_0(\mathbf{x}) + \sum \limits_{i=1}^m \lambda_i f_i(\mathbf{x}) + \sum \limits_{i=1}^p \nu_i h_i(\mathbf{x})\]- $\mathbf{x} \in \mathbb{R}^n, \lambda \in \mathbb{R}^m, \nu \in \mathbb{R}^p$
- $L: \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R}^p \rightarrow \mathbb{R}$
Primal Problem의 제약조건을 Irritation으로 해석해 보자.
이 경우 Primal Problem은 다음의 Unconstrained 문제로 바꿀 수 있다
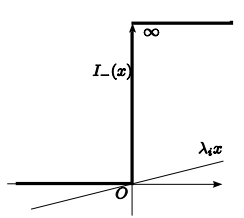
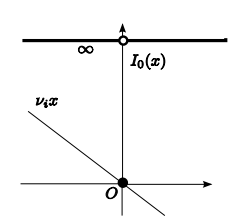
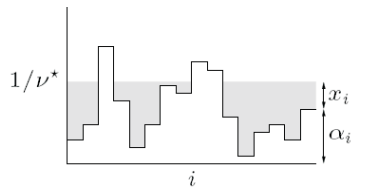
“Primal Problem = $f_0(\mathbf{x}) + \sum \limits_i I_-(f_i(\mathbf{x})) + \sum \limits_i I_0(h_i(\mathbf{x}))$”
$I_-(x)$ $I_0(x)$ $I_-(x) \geq \lambda x \geq 0$ $I_0(x) \geq \nu x$ 이때, 위의 그림과 같이 모든 $\mathbf{x}$에 대해
$f_0(\mathbf{x}) + \sum \limits_i I_-(f_i(\mathbf{x})) + \sum \limits_i I_0(h_i(\mathbf{x})) \geq f_0(\mathbf{x}) + \sum \limits_i \lambda_i f_i(\mathbf{x}) + \sum \limits_i \nu_i h_i(\mathbf{x})$
이 성립하는 것을 알 수 있다.즉, $\tilde{x}$가 Primal Problem에서 Feasible $(f_i(\tilde{x}) \leq 0, h_i(\tilde{x})=0)$하고, $\lambda \geq 0$이면,
$f_0(\tilde{x}) \geq L(\tilde{x}, \lambda, \nu) \geq \inf \limits_{\mathbf{x} \in \mathbb{R}^n} L(\mathbf{x}, \lambda, \nu) = g(\lambda, \nu)$
이 성립한다.즉, Primal Problem의 해를 $p^*$라고 하고, Dual Problem의 해를 $d^*$라고 하면,
$d^* \leq p^*$를 항상 만족하는 것을 알 수 있다.
2) Lagrangian Dual Function
\[g(\lambda, \nu) = \inf \limits_{\mathbf{x} \in \mathbb{R}^n} L(\mathbf{x}, \lambda, \nu)\]- $g: \mathbb{R}^m \times \mathbb{R}^p \rightarrow \mathbb{R}$
위의 $d^*$를 정의하기 위한 문제를 Lagrangian Dual Function이라고 부른다.
Lagrangian Dual Function의 특징
- 원래 함수 $f$관계없이 $\lambda, \nu$에 대해 항상 Concave함수이다.
($\mathbf{x}$에 대해 affine function들의 Pointwise Infimum이기 때문)- lower bound property
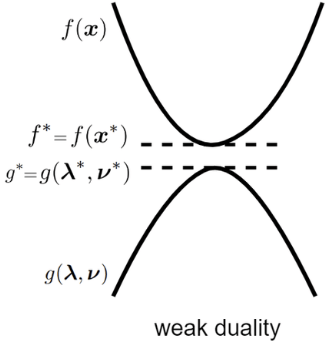
$g(\lambda, \nu) \leq f(\mathbf{x}^*) \qquad , if \;\; \lambda \geq 0$Weak & Strong Duality
Lower Bound Property는 Primal Function과 Dual Function의 관계를 나타낸다.
이를 더 자세히 살펴보자.
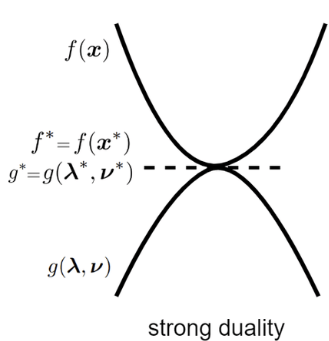
Weak Duality Strong Duality DualityGap $d^* \leq p^*$ $d^* = p^*$ Condition Any Slater’s Constraint
($f_i(\mathbf{x})$는 Convex)(Duality Gap: $d^* - p^*$ )
Lagrangian Dual Problem
\[\text{maximize} \quad g(\lambda, \nu)\\ \text{subject to} \quad\; \lambda \geq 0\]즉, Lagrangian Dual Problem을 풀면, 원래 문제의 정답을 어느정도 알 수 있게 된다.
3) Examples:
| Problem | Dual Function |
|---|---|
| ⅰ. Least-Norm Solution \(\quad \text{minimize} \quad\; \mathbf{x}^T\mathbf{x} \\\quad \text{subject to} \quad A\mathbf{x} = \mathbf{b}\) | \(\mathcal{L}(\mathbf{x}, \nu) = \mathbf{x}^T\mathbf{x} + \nu^T(A\mathbf{x} - \mathbf{b}) \\ \nabla_\mathbf{x} \mathcal{L}(\mathbf{x}, \nu) = 2\mathbf{x} + A^T \nu = 0 \\ \qquad \qquad \; \rightarrow \therefore \mathbf{x} = -\frac{1}{2A^T\nu} \\ g(\nu) = \mathcal{L}(\mathbf{x} = -\frac{1}{2A^T\nu}, \nu) = -\frac{1}{4\nu^TAA^T\nu} - \mathbf{b}^T\nu\) |
| ⅱ. Linear Programming \(\quad \text{minimize} \quad\; \mathbf{c}^T\mathbf{x} \\ \quad \text{subject to} \quad A\mathbf{x} = \mathbf{b}, \\ \qquad \qquad \qquad\; -\mathbf{x} \leq 0\) | \(\mathcal{L}(\mathbf{x}, \lambda, \nu) = \mathbf{c}^T\mathbf{x} + \nu^T(A\mathbf{x} - \mathbf{b}) - \lambda^T \mathbf{x} \\ \qquad \qquad = -\mathbf{b}^T \nu + (\mathbf{c} + A^T\nu - \lambda)^T \mathbf{x} \\ \qquad \qquad \rightarrow \mathbf{x}\text{에 대한 1차함수} \\ g(\nu) = \inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \lambda, \nu) = \begin{cases} -\mathbf{b}^T \nu, \quad (\mathbf{c} + A^T\nu - \lambda = 0) \\ -\infty, \quad\quad (\text{otherwise})\end{cases}\) |
| ⅲ. Equality Constrained Norm \(\quad \text{minimize} \quad\; \Vert \mathbf{x} \Vert \\\quad \text{subject to} \quad A\mathbf{x} = \mathbf{b}\) | \(\mathcal{L}(\mathbf{x}, \nu) = \Vert \mathbf{x} \Vert + \nu^T(A\mathbf{x} - \mathbf{b}) \\ \qquad \quad \geq \Vert \mathbf{x} \Vert + \Vert A^T \nu \Vert_* \Vert \mathbf{x} \Vert - \mathbf{b}^T\nu \\ \qquad \quad \geq (1-\Vert A^T \nu \Vert_* ) \Vert \mathbf{x} \Vert - \mathbf{b}^T \nu \\ \qquad \quad \rightarrow \mathbf{x}\text{에 대한 2차함수} \\ g(\nu) = \inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \nu) = \begin{cases} -\mathbf{b}^T \nu, \quad (\Vert A^T \nu \Vert_* \leq 1) \\ -\infty, \quad\quad (\text{otherwise})\end{cases}\) |
| ⅳ. Entropy Maximization \(\quad \text{minimize} \quad\; \sum \limits_{i=1}^n x_i log(x_i) \\ \quad \text{subject to} \quad \textbf{1}^T \mathbf{x} = 1, \\ \qquad \qquad \qquad\; A\mathbf{x} \leq \mathbf{b}\) | \(\mathcal{L}(\mathbf{x}, \lambda, \nu) = \sum \limits_{i=1}^n x_i log(x_i) + \nu^T(\textbf{1}^T\mathbf{x} - 1) + \lambda^T(A\mathbf{x} - \mathbf{b}) \\ \nabla_{x_i} \mathcal{L}(\mathbf{x}, \lambda, \nu) = log(x_i) + 1 + \nu^T + \lambda^T \mathbf{a}_i = 0 \\ \qquad \qquad \quad \;\; \rightarrow \therefore x_i = e^{-(1+\nu^T + \lambda^T \mathbf{a}_i)}\\ g(\lambda, \nu) = \inf \limits_x \mathcal{L}(\mathbf{x}, \lambda, \nu) = -\nu - \lambda^T \mathbf{b} - \sum \limits_{i=1}^n e^{-(1+ \nu + \mathbf{a}_i^T \lambda)}\\ ---------- \\ \text{Dual Problem} \\ \text{Maximize:} \quad g(\lambda, \nu) = -\nu - \lambda^T \mathbf{b} - \sum \limits_{i=1}^n e^{-(1+ \nu + \mathbf{a}_i^T \lambda)} \\ \lambda \geq 0 \text{이지만 } \nu \text{에 대해서는 제약 조건 존재 X} \\ \rightarrow \nu \text{에 대해서 먼저 Maximize} \\ \rightarrow \nabla_\nu g(\lambda, \nu) = 0 \\ \rightarrow \text{Maximize:} \quad -\mathbf{b}^T \lambda - log(\sum \limits_{i=1}^m e^{-\mathbf{a_i}^T \lambda})\) |
| ⅴ. Two Way Partitioning \(\quad \text{minimize} \quad\; \mathbf{x}^TW\mathbf{x} \\ \quad \text{subject to} \quad x_i^2 = 1\) ※ $\mathbf{x}^TW\mathbf{x} = \sum \limits_{(i, j)} x_i x_j w_{i, j}$ | \(\mathcal{L}(\mathbf{x}, \nu) = \mathbf{x}^TW\mathbf{x} + \nu^T \sum \limits_i(x_i^2-1) \\ \qquad \quad = \mathbf{x}^T W \mathbf{x} + \nu^T \sum \limits_i x_i^2 - \textbf{1}^T \nu \\ \qquad \quad = \mathbf{x}^T W \mathbf{x} + \mathbf{x}^T diag(\nu) \mathbf{x} - \textbf{1}^T \nu \\ \qquad \quad = \mathbf{x}^T (W + diag(\nu)) \mathbf{x} - \textbf{1}^T \nu \\ \qquad \quad \rightarrow \mathbf{x}\text{에 대한 2차함수}\\ g(\nu) = \inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \nu) = \begin{cases} -\mathbf{1}^T \nu, \quad (W + diag(\nu) \succeq 0) \\ -\infty, \quad\quad (\text{otherwise})\end{cases} \\ ---------- \\ \text{Dual Problem} \\ W + diag(\nu) = U \Lambda U^T - diag(\nu)I \\ \qquad \qquad \quad\;\, = U \Lambda U^T - diag(\nu) UU^T \\ \qquad \qquad \quad\;\, = U(\Lambda - diag(\nu))U^T \\ \qquad \qquad \quad\;\, \rightarrow diag(\nu) = \lambda_{\text{min}}I \text{일 때 PSD (}\lambda_\text{min}\text{은 W의 최소 고유값)} \\ \therefore g(\nu) = -\textbf{1} \cdot \lambda_\text{min} I = n \lambda_\text{min}\) |
※ Dual Norm
$\Vert x \Vert$의 Dual Norm은 $\Vert x \Vert_*$로 나타낸다.
- Dual Norm의 정의
- $\Vert x \Vert_p$와 $\Vert x \Vert_q$가 $\frac{1}{p} + \frac{1}{q} = 1$일 때, 두 Norm은 Dual Norm 관계이다.
- Dual Norm의 정의
- Dual Norm의 특징
- $\mathbf{c}^T \mathbf{x} \leq \Vert \mathbf{c} \Vert_* \Vert \mathbf{x} \Vert$
- Dual Norm의 특징
※ 위의 이유로 LP문제와 QP문제의 Dual Problem은 각각 LP와 QP이다.
2. KKT Condition
Karush-Kuhn-Tucker Conditions
1) 정의
| 1 | Primal Constraints | $f_i(\mathbf{x}) \leq 0$ |
| 2 | Dual Constraints | $\lambda \geq 0$ |
| 3 | Complementary Slackness | $\lambda_i f_i(\mathbf{x}) = 0$ |
| 4 | Gradient of Lagrangian | $\nabla_\mathbf{x} \mathcal{L} = 0$ |
이때, 원래의 문제가 Strong Duality를 만족하고 $\mathcal{L}(\mathbf{x}, \lambda, \nu)$가 Convex함수라고 할 때,
\[\text{KKT Condition Hold} \Leftrightarrow \text{Optimal}\]다시말해, $\mathbf{x}^*, \lambda^*, \nu^*$가 KKT Condition을 만족한다는 것은 원래 문제의 해,
즉 Optimal이라는 것과 필요 충분 조건이다.Complementary Slackness
Strong Duality를 만족한다고 하자.
$f_0(\mathbf{x}^*) = g(\lambda^*, \nu^*) = \inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \lambda^*, \nu^*) = \inf \limits_\mathbf{x} (f_0(\mathbf{x}) + \sum \limits_{i=1}^m \lambda_i^* f_i(\mathbf{x}) + \sum \limits_{i=1}^p \nu_i^* h_i(\mathbf{x}))$이때, $\inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \lambda^*, \nu^*) \leq \mathcal{L}(\mathbf{x}^*, \lambda^*, \nu^*) (= f_0(\mathbf{x}^*) + \sum \limits_{i=1}^m \lambda_i^* f_i(\mathbf{x}^*) + \sum \limits_{i=1}^p \nu_i^* h_i(\mathbf{x}^*))$ 이고,
$\lambda_i \geq 0, f_i(\mathbf{x}) \leq 0, h_i(\mathbf{x}) = 0$이므로 $\mathcal{L}(\mathbf{x}^*, \lambda^*, \nu^*) \leq f_0(\mathbf{x}^*)$가 성립된다.즉 $f_0(\mathbf{x}^*) \leq \mathcal{L}(\mathbf{x}^*, \lambda^*, \nu^*) \leq f_0(\mathbf{x}^*)$ 이므로, $f_0(\mathbf{x}^*) = \mathcal{L}(\mathbf{x}^*, \lambda^*, \nu^*)$ 이고
결과적으로 $\lambda_i^* f_i(\mathbf{x}^*) = 0$이 항상 성립한다.
(이는 $\lambda_i$와 $f_i(\mathbf{x}^*)$가 모두 0이 아닌 경우는 없다는 것을 의미한다.)Gradient of Lagrangian
$\inf \limits_\mathbf{x} \mathcal{L}(\mathbf{x}, \lambda^*, \nu^*) = \mathcal{L}(\mathbf{x}^*, \lambda^*, \nu^*)$이고, $f_i(\mathbf{x})$는 Convex Function이므로
이 문제는 Unconstrained Minimization Problem이다.즉, Strong Duality가 Hold될 경우 $\nabla_\mathbf{x} \mathcal{L} = 0$ 이 성립되어야 한다.
2) Examples
| Problem | KKT Condition ($\mathbf{x}^*, \lambda^*, \nu^*$ 구하기) |
|---|---|
| ⅰ. Equality Constrained QP \(\quad \text{minimize} \quad\; \frac{1}{2}\mathbf{x}^TP\mathbf{x} + q^T \mathbf{x} + r \\ \quad \text{subject to} \quad A\mathbf{x} = \mathbf{b}\) | \(1. \text{Primal Feasible} \\ \quad \rightarrow A\mathbf{x}^* = \mathbf{b} \\ 2. \text{Dual Feasible} \\ \quad \rightarrow (\text{Inequality 조건 없음}) \\ 3. \text{Complementary Slackness} \\ \quad \rightarrow (\text{Inequality 조건 없음}) \\ 4. \text{Gradient of Lagrangian} \\ \quad \rightarrow P\mathbf{x}^* + q + A^T \nu^* = 0\) |
| ⅱ. Waterfilling \(\quad \text{minimize} \quad\; -\sum \limits_{i=1}^n log(x_i + \alpha_i)\\ \quad \text{subject to} \quad \mathbf{x} \geq 0, \\ \qquad \qquad \qquad \mathbf{1}^T \mathbf{x} = 1\) ※ $\mathbf{x}$는 나누어 주는 Resource, $\quad \alpha$는 초기 자산이라고 생각할 때, $\quad$ 효용($log(x_i + \alpha_i)$)을 $\quad$ 최대화 하는 문제로 생각 가능 $\quad$(최대 다수의 최대 행복) ※ 참고그림  | \(1. \text{Primal Feasible} \\ \quad \rightarrow \mathbf{x}^* \geq 0, \; \mathbf{1}^T \mathbf{x}^* = 1 \\ 2. \text{Dual Feasible} \\ \quad \rightarrow \lambda \geq 0 \\ 3. \text{Complementary Slackness} \\ \quad \rightarrow \lambda_i x_i = 0 \\ 4. \text{Gradient of Lagrangian} \\ \quad \rightarrow \nabla_{x_i} \mathcal{L} = \nabla_{x_i}(-\sum \limits_{i=1}^n log(x_i + \alpha_i) - \lambda^T \mathbf{x} + \nu^T(\textbf{1}^T\mathbf{x} - 1))\\ \qquad \qquad \;\;\, = -\frac{1}{x_i + \alpha_i} - \lambda_i + \nu = 0 \\ \quad \text{ⅰ.} \nu < \frac{1}{\alpha_i} \text{일 경우} \rightarrow \lambda_i = 0, x_i = \frac{1}{\nu} - \alpha_i \\ \quad \quad (\because \text{if }\; \lambda_i > 0 \overset{KKT-3}{\rightarrow} x_i = 0 \overset{KKT-4}{\rightarrow} \nu = \frac{1}{\alpha_i} + \lambda_i \overset{\text{모순}}{\rightarrow} \lambda_i = 0)\) \(\quad \text{ⅱ.} \nu \geq \frac{1}{\alpha_i} \text{일 경우} \rightarrow x_i = 0 \\ \quad \quad (\because \text{if }\; x_i > 0 \overset{KKT-3}{\rightarrow} \lambda_i = 0 \overset{KKT-4}{\rightarrow} \nu = \frac{1}{\alpha_i + x_i} \overset{\text{모순}}{\rightarrow} x_i = 0)\) $\Rightarrow x_i = \max(0, \frac{1}{\nu} - \alpha_i) = [\frac{1}{\nu} - \alpha_i]^+$ |
| ⅲ. Norm Minimization \(\quad \text{minimize} \quad\; \Vert A\mathbf{x} + \mathbf{b}\Vert \\ \qquad \Downarrow \\ \;\;\, \text{minimize} \quad\; \Vert \mathbf{y} \Vert \\ \quad \text{subject to} \quad \mathbf{y} = A\mathbf{x} + \mathbf{b}\) | [과제 예제] |
※ Maximize문제는 항상 Minimize문제로 바꾸어 풀자
※ Constraint가 없어서 Duality를 활용할 수 없을 경우 새로운 변수를 통해 Equality Constrained문제로 바꿀 수 있다.
$\quad \rightarrow$이때, Dual Problem의 infimum은 두 변수를 동시에 최소화 하도록 함