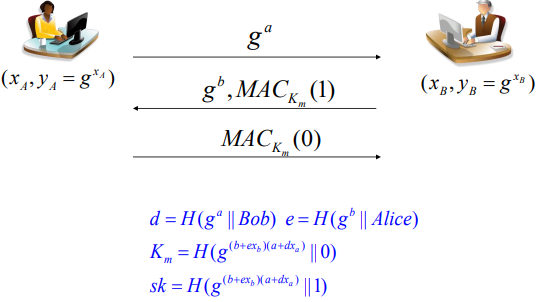포스트

6. Key Exchange & Public Key Infrastructure

게시
By UI-JIN KIM 19 분읽는 시간

1. Key Exchange

안전한 통신을 위해 두 당사자가 암호화 키를 어떻게 공유하는지, 그리고 그 안전성을 평가하는 기준과 관련 프로토콜들을 알아보자.

1) Concept

alt text

은행-사용자와 같이 서로 떨어진 당사자간의 통신 메시지를 암호화 하기 위해 사용할 Session Key($Sk$)를 안전하게 나누어 갖는 상황을 말한다.

Adversary

공격자는 다음과 같은 능력을 지녔다고 가정한다.

  • Send: 메시지를 가로채거나 조작하여 전송
    $\quad \rightarrow \text{Send}(\pi_i^j, M)$
  • Corrupt: 사용자의 개인 키 탈취
    $\quad \rightarrow \text{Corrupt}(P_i)$
  • Reveal: 특정 세션 키 탈취
    $\quad \rightarrow \text{Reveal}(\pi_i^j)$
  • Test: 키가 진짜인지 랜덤인지 구별 가능
    $\quad \rightarrow \text{Test}(\pi_i^j)$

※ $\pi_i^j$: 사용자 i의 j번째 세션(인스턴스).

Security Notation

키 교환 프로토콜이 안전성은 다음 5가지 조건을 얼마나 만족하는지에 따라 달라진다.

  • IA(Implicit Authentication): 지정된 당사자만 세션 키를 얻을 수 있어야 함
  • KI(Key Independence): 과거의 세션 키가 노출되어도 다른 세션 키는 안전해야 함
  • UKS(Unknown Key Share): A와 통신한다고 생각했는데, 실제로는 B와 키를 공유하며 통신하는 상황이 없어야 함
  • FS(Forward Secrecy): 개인키가 탈취당해도 과거의 세션키를 얻을 수 없어야 함
  • SSR(Session State Reveal): 키를 만드는 과정에서 사용된 난수가 노출되어도 최종 세션 키는 안전해야 함

Types of Key Exchange

  • Key Transfer: 한쪽이 키를 생성해 암호화하여 상대방에게 보내주는 방식
  • Key Agreement: 양쪽이 정보를 주고받아 공동으로 키를 생성하는 방식(Diffie-Hellman)
  • 패스워드 기반, 공개키 기반, 그룹 키 교환 등…

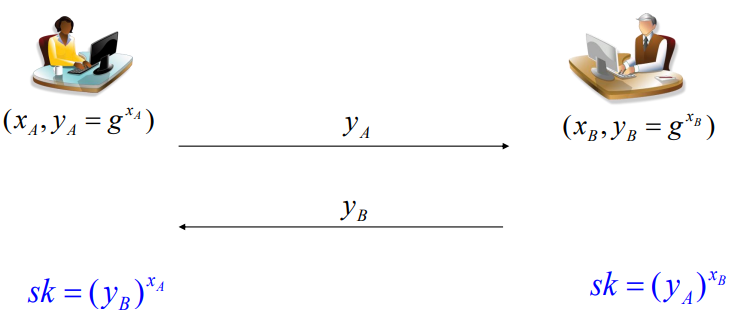
2) Diffie-Hellman

Diffie-HellmanEncrypted Key Exchange
alt textalt text
  1. Alice
    $x_A$를 개인 키로하여 $y_A = g^{x_A}$를 Bob에게 전송한다.
  2. Bob
    $x_B$를 개인 키로하여 $y_B = g^{x_B}$를 Alice에게 전송한다.
  3. Session key 생성
    Alice는 $Sk = (y_B)^{x_A} = g^{x_A \cdot x_B}$로 키를 생성한다.
    Bob은 $Sk = (y_A)^{x_B} = g^{x_A \cdot x_B}$로 키를 생성한다.
  • 취약점
    FS: 이러한 방식은 개인 키가 탈취당하면 세션 키를 곧바로 만들어낼 수 있기 때문에 FS에 취약하다.
    UKS: 신원 확인 정보가 키 교환에 포함되어 있지 않기 때문에, UKS 공격에도 취약하다.

Encrypted Key Exchange

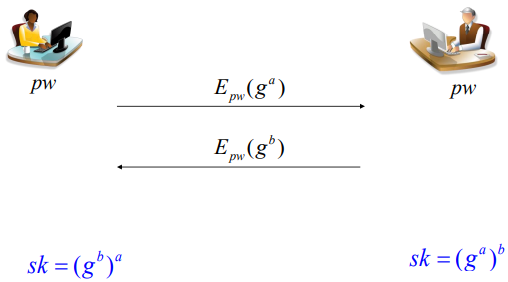
만약 두 사람이 공유된 대칭 키를 가지고 있으면 다음과 같은 방식으로 FS에 강인한 키 교환 프로토콜을 만들 수 있다.

  1. Alice
    $E_{sk}(g^a)$를 계산하여 Bob에게 전송(a는 Alice가 선택한 랜덤 값)
  2. Bob
    $E_{sk}(g^b)$를 계산하여 Alice에게 전송(b는 Bob이 선택한 랜덤 값)
  3. Session Key 생성
    Alice는 $Sk = (g^b)^a$로 키를 생성한다.
    Bob은 $Sk = (g^a)^b$로 키를 생성한다.

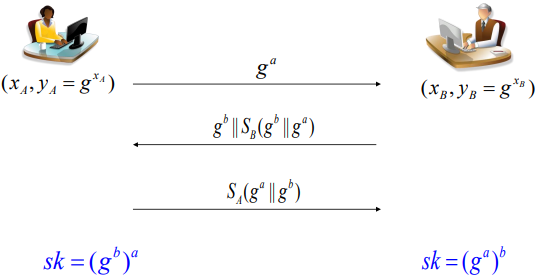
3) BCK(STOC98)

BCK(STOC98)HMQV-C(Crypto05)
alt textalt text

BCK 프로토콜은 기본 Diffie-Hellman에 전자서명과 임시 키(a/b)를 도입하여 Forward Secrecy를 보장하는 방식이다.
($x_A, x_B$는 서명에 사용되는 장기 비밀키이고, $a, b$는 세션마다 바뀌는 임시 비밀값)

  1. Alice
    임시 비밀값(난수) $a$를 선택하여 $g^a$를 Bob에게 전송
  2. Bob
    임시 비밀값(난수) $b$를 선택하고, $g^b$와 함께, 자신이 생성한 전자서명 $S_{x_B}(g^b \Vert g^a)$를 Alice에게 전송
  3. Alice
    Bob의 서명을 확인한 후, 자신의 전자서명 $S_{x_A}(g^a \Vert g^b)$를 Bob에게 전송
  4. Session Key 생성
    Alice는 $sk = (g^b)^a = g^{ab}$로 키를 생성
    Bob은 $sk = (g^a)^b = g^{ab}$로 키를 생성

이때, a, b, 는 바로 삭제되기 때문에 $x_A, x_B$가 노출되어도 $sk$를 알 수 없다.

  • 취약점
    SSR: 키를 만드는 과정에서 사용된 난수가 노출되면 session key를 쉽게 복원당할 수 있다.

HMQV-C(Crypto05)

HMQV-C는 해시 함수를 이용해 인증을 수행하며, FS와 SSR을 모두 만족하는 매우 안전한 프로토콜이다.

  1. Alice
    임시 비밀값(난수) $a$를 선택하여 $g^a$를 Bob에게 전송한다.
  2. Bob
    임시 비밀값(난수) $b$를 선택하여 $g^b$를 만들어 Alice에게 전송한다.
    (이때, 대칭키를 활용해 데이터의 무결성을 보장하기 위한 $MAC_{K_m}(1)$을 함께 보냄)

  3. Session Key 생성
    ⅰ) 보조 값 계산 (Hash): $d = H(g^a || \text{Bob})$, $e = H(g^b || \text{Alice})$
    ⅱ) Alice는 다음과 같이 키를 생성
    $\quad$: 공유 비밀값 $\sigma = (g^b \cdot y_B^e)^{a + d x_A} = g^{(b + e x_B)(a + d x_A)}$
    $\quad$: 세션 키 $sk = H(\sigma || 1)$

  4. Bob은 다음과 같이 키를 생성
    $\quad$: 공유 비밀값 $\sigma = (g^a \cdot y_A^d)^{b + e x_B} = g^{(a + d x_A)(b + e x_B)}$ $\quad$: 세션 키 $sk = H(\sigma || 1)$

이 경우, 세션 키를 생성할 때 난수와 비밀키를 같이 활용하기 때문에 SSR에 안전하다.

※ 만약 난수와 비밀키를 동시에 탈취당할 경우 공격을 당할수는 있다.

2. Public Key Infrastructure

공개키의 문제점은, 단순히 공개키를 게시판에 올려두면 공격자가 키를 바꿔치기해도 사용자가 이를 알아챌 수 없다는 점이다. 즉, 사용자가 잘못된 공개키로 메시지를 암호화 한다면, 공격자에 의해 쉽게 복호화될 수 있다.

이를 위해, 신뢰할 수 있는 제 3자(인증기관, CA)가 ‘이 공개키는 A의 것이 맞다’라고 보증하는 전자서명이 필요하고, 이러한 기반 시설이 필요하다.

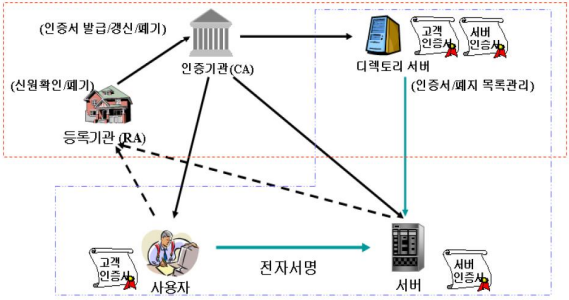
1) PKI Structure

alt text

  • 인증기관(CA, Certification Authority)
    인증서를 발급(생성), 갱신, 폐기 및 관리의 주체
  • 등록기관 (RA, Registration Authority)
    사용자의 신분을 확인(대면 확인 등)하고 CA와 사용자 사이의 인터페이스 역할
  • 디렉토리 (Directory)
    인증서와 CRL(폐기 목록)이 저장되어 공개되는 저장소

PKI Topology

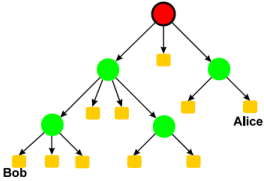
alt textalt text
  • Hierarchical Infrastructure
    최상위 root CA를 정점으로 트리 형태로 연결된 구조(★ root의 서명은 모두가 알고 있다고 가정해야 한다.)
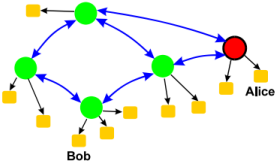
  • Mesh Infrastructure
    CA들끼리 상호 인증을 통해 그물망처럼 연결된 구조

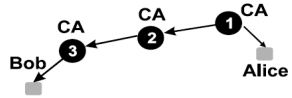
2) Certificate Authentication Path

alt textalt text

사용자(Alice)가 다른 사용자(Bob)의 공개키가 진짜인지 믿기 위해서는, 자신이 신뢰하는 최상위 기관(Root CA)부터 Bob까지 이어지는 인증 경로 검증을 거쳐야 한다.

예를 들어 Alice가 CA1을 Trust Anchor로 설정해 두었다고 하자.
그리고 Bob의 인증서를 발급해준 CA3의 인증서가 믿을만한지 확인하기 위해 CA3부터 CA1까지 이어지는지를 확인하면 된다.
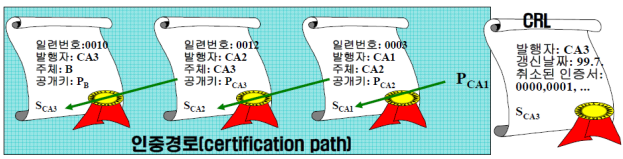
또한 root CA의 경우, 자신의 신원을 보증해줄 CA가 없기 때문에 스스로 자신의 공개키($P_{CA1}$)에 대한 서명($S_{CA1}$)을 스스로 한다. 이를 self-certificate라고 한다.

이때, 검증해야할 내용은 다음과 같다.

  • 전자서명 검증
  • 유효기관 확인
  • 발급자 및 소유자 확인
  • 인증서 상태 확인(CLR)을 조회하여 폐기 목록에 있는지 확인
  • 정책필드 및 확장필드 확인

이때, OCSP(Online Certificate Status Protocol)을 확인하여 실시간 상태를 확인해볼수도 있다.

1단계: CA 구축 (Implementation)

  • 핵심: 인증기관(CA) 자체의 신뢰성 확보.
  • 내용: 물리적 통제 구역 내에 정책 관리 시스템과 암호 모듈(HSM)을 설치하여 CA의 키와 자체 인증서를 안전하게 생성하고, 이를 디렉토리(공개 저장소)에 게시

2단계: 등록 및 발급 (Registration & Issuing)

  • 핵심: 사용자의 신원 확인과 키 소유 검증.
  • 내용: 사용자(A)가 ⅰ) 인증서를 요구하면, ⅱ) 등록기관(RA)은 A의 신원을 확인하고, 해당 공개키에 대한 비밀키를 실제 소유했는지 확인한다. ⅲ) 그리고 인증서를 발행하고 자신의 서명과 함께 공개 디렉토리에 보관한다.

3단계: 사용 및 검증 (Digital Signatures)

  • 핵심: 상대방 인증서의 유효성(폐기 여부 포함) 검사
  • 내용: 사용자(B)는 A의 서명을 검증할 때, 디렉토리에서 CRL(폐기 목록)과 인증 경로(상위 CA 인증서들)를 다운로드하여 서명의 유효성, 만료 여부, 폐기 여부를 최종 확인

3. Public Key Cryptography

위의 PKI는 다음과 같은 문제점을 가지고 있다.

  • 인증서 관리 및 검증 문제
    CRL을 관리하기 위해 많은 비용이 소모되고, 주기적인 인증서 갱신 작업은 편의성이 떨어짐
  • 인증기관 권한 문제
    CA의 권한이 지나치기 때문에, CA가 공격당할 경우 보안 사고의 규모가 커짐
  • 저성능 기기 문제
    인증서 검증과 같은 부가적인 연산은 저성능 기기에서는 수행될 수 없음

이를 위해 인증서 없이 사용자의 ID나 속성을 활용하는 암호 기술들이 등장하였다.

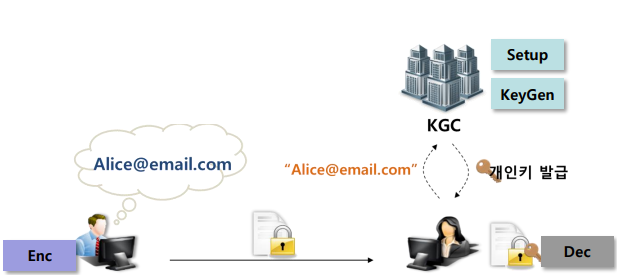
1) ID 기반 암호 (IBC, Identity-Based Cryptography)

alt text

사용자의 이메일 주소, 학번 등 신원정보(ID) 자체를 공개키로 사용하는 방식

Identity-Based Encryption from the Weil Pairing

IBE에서는 KGC(Key Generation Center)라는 기관이 존재한다. 여기서는 사용자의 ID를 기반으로 개인키를 발급하는 역할을 한다.

  • KGC
    자산: Public Key($P_{pub}$)와 Secret Key($s$)를 가지고 있음
    역할: 사용자의 ID와 자신의 Secret Key를 가지고 사용자의 Secret Key($sk$)를 발급

  • 송신자
    자산: 임의의 난수($r$)를 생성하여 사용 역할: KGC의 Public Key와 사용자의 ID, 난수 r을 가지고 메시지를 암호화

  • 수신자(사용자)
    자산: Secret Key($sk$)를 가지고 있음
    역할: 상대가 보낸 암호문을 Secret Key를 가지고 복호화

  1. Setup
    Parameter(PP) = $[e, H_1, H_2, P, P_{pub}]$ (사용 함수들, Public Key($P_{pub} = sP$))
    Master Key(MSK) = $s$
  2. Secret Key Generation
    $sk = s \cdot H_1(ID)$
  3. Encryption
    $C = [C_1, C_2] = [rP, M \oplus H_2(e(H_1(ID), P_{pub})^r)]$
  4. Decryption
    $M = C_2 \oplus H_2(e(C_1, sk))$

※ Encryption 원리

  • Bilinear Map 함수: $e(aP, bQ) = e(P, Q)^{ab}$

Bilinear함수를 활용하면 $e(H_1(ID), P_{pub})^r = e(H_1(ID), sP)^r = e(sH_1(ID), P)^r = e(sk, P)^r = e(sk, rP) = e(sk, C_1)$ 이 성립한다.

이때, r은 일회적으로 사용하는 무작위 랜덤 값이다. 즉, 상대방은 public Key만을 활용해 암호문을 계산할 수 있다.
하지만 이를 복호화 해야하는 공격자 입장에서는 r을 알지 못하기 때문에 이를 다시 계산하는 것은 불가능에 가깝다.
반면에 수신자는 Bilinear Map의 특성을 이용해 secret key만 알고 있다면 이를 쉽게 복호화할 수 있다.

결과적으로 데이터를 보내려는 사람은 해당 Public Key가 Alice의 키가 맞는 키인지 검증할 필요가 없고, 기관의 Key만 있으면 된다.

특징

  • 전자서명
    사용자가 자신의 sk를 가지고 서명하면, 검증자가 사용자의 ID를 가지고 복호화 하는 방식으로 서명 알고리즘을 설계할 수 있다.
  • 계층적 ID기반 암호
    PKI와 마찬가지로, 계층적으로 KGC를 구성할 수도 있다. 이 경우 ID는 상위 KGC를 점차 포함하게끔 설정해야한다.
    (KGC1 - KGC2 - USER1일 경우 $\rightarrow$ ID = $[ID_{KGC2}, ID_{USER1}]$)

문제점

  • Key Escrow문제: MSK로부터 개인키가 생성되기 때문에, KGC는 모든 사용자에 대한 개인키를 복제할 수 있음
  • Key 폐기 문제: 사용자가 탈퇴할 경우 발급된 키를 폐기하는게 불가능

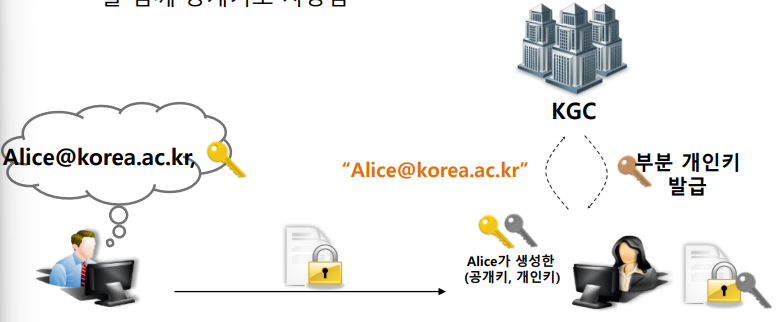
2) 무인증서 암호 (CLC, Certificateless Cryptography)

alt text

PKI의 인증서 관리 문제와 IBC의 키 위탁 문제를 동시에 해결하기 위해 제안된 방식

  • 키 생성 방식
    • 공개키: 사용자의 ID + 사용자가 직접 생성한 난수
    • 개인키: KGC가 준 부분 개인키 + 사용자가 만든 비밀 정보를 결합하여 생성
  • 장점
    • KGC는 부분적인 키만 알고 있으므로 사용자의 최종 개인키를 알 수 없어 키 위탁 문제 해결 가능
  • 한계점
    • 여전히 키 폐기 문제와 효율성 문제가 남아 있음

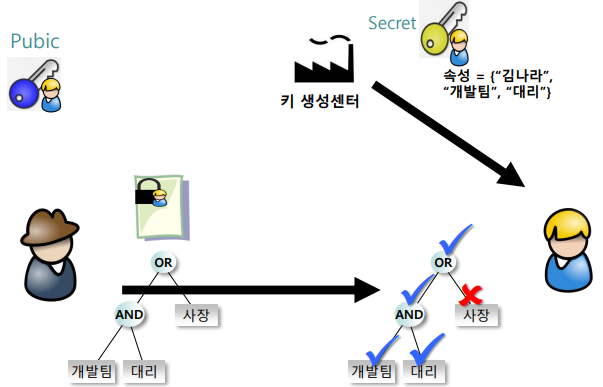
3) 속성 기반 암호 (ABC, Attribute-Based Cryptography)

alt text

특정 ID가 아니라, 사용자의 속성(Attribute)과 접근 제어 정책(Access Policy)을 기반으로 암호화 및 복호화를 수행

  • 작동 원리
    • 예: “개발팀” AND (“대리” OR “과장”)과 같은 조건을 만족하는 사용자만 복호화할 수 있도록 설정

장점 - 복잡한 환경에서 유연한 접근 제어가 가능합니다. - 클라우드 검색: 암호화된 데이터에 대해 익명성을 유지하며 키워드 검색을 수행하는 데 활용

Math, Cryptography
cryptography key exchange public key infrastructure pki
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.