3. Generative Model

Generative Model

Unsupervised Learning

생성형 모델은 Unsupervised Learning중 한 종류이다.
즉, Training Data에 Label이 존재하지 않다.

그렇다면 어떻게 학습을 진행할 수 있을까?

생성형 모델의 가장 기본적인 Concept는 입력값에 대한 Latent(잠재) Vector를 학습하는 것이다.
즉, 입력값을 잘 표현할 수 있는 잠재적인 정보를 학습하고, 이를 생성에 활용할 수 있도록 한다.

\[\mathbb{P(\mathbf{x})} = \int \mathbb{P}_w(\mathbf{x}, z) dz\]

※ $\mathbf{x}$: Input (ex. 말, 단어, 목소리, … 등 “형태”)
$\quad z$: Latent Vector (ex. 생각, … 등 “개념”)

PPCA

즉, 생성형 모델은 아래와 같이 모델링 할 수 있다.

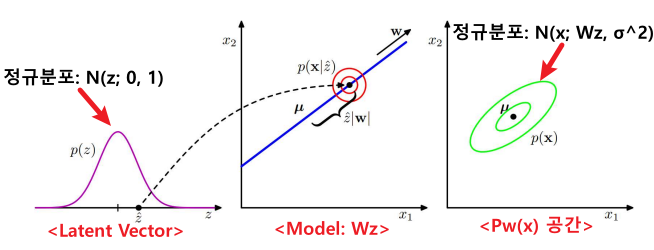
$\mathbf{z}$	$P_w(\mathbf{x} \vert \mathbf{z})$ (Generation)	$P_w(x)$
잠재벡터 $\mathbf{z}$는 정규분포라고 가정한다.	잠재벡터에 대한 출력값(=입력값)을 $\mathbf{W} \cdot \mathbf{z}$로 모델링한다. 이 때, 가우시안 잡음이 추가된다. (가우시안 잡음 = $\sigma^2 I$)	Marginalization $P_w(x) = \int P_w(\mathbf{x}, \mathbf{z}) d\mathbf{z}$ $\qquad \;\;\; = \int P_w(\mathbf{x} \vert \mathbf{z})P(\mathbf{z}) d\mathbf{z}$ $\qquad \;\;\; = \mathcal{N}(\mathbf{x}; 0, \mathbf{WW}^T + \sigma^2I)$
$P(\mathbf{z}) = \mathcal{N}(\mathbf{z}; 0, I)$	$P_w(\mathbf{x} \vert \mathbf{z}) = \mathcal{N}(\mathbf{x}; \mathbf{W}\mathbf{z}, \sigma^2I)$	$P_w(x) = \mathcal{N}(\mathbf{x}; 0, \mathbf{WW}^T + \sigma^2I)$

• Generation
  

  Latent Vector로 Input을 복원하는 것 ($\mathbb{P}_w(\mathbf{x} \vert z)$)

• Training
  

  $\text{log}(P_w(x)) = \text{log}(\mathcal{N}(\mathbf{x}; 0, \mathbf{WW}^T + \sigma^2I))$ 를 Maximize하므로써 진행된다.

• Inference
  

  Input에서 Latent Vector를 추론하는 것 ($\mathbb{P}(z \vert \mathbf{x})$)
  $\rightarrow \hat{z} = \int P_w(\mathbf{z} \vert \mathbf{x}) \mathbf{x} d\mathbf{x}$

---

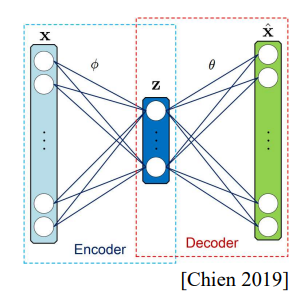
1. VAE

Auto Encoder	Variational Auto Encoder
입력 $\mathbf{x}$을 Encoder에 넣어Latent Vector $\mathbf{z}$, $(dim(\mathbf{z}) \ll dim(\mathbf{x}))$로 압축(손실압축)하고, ecoder에서는 이 Latent Vector $\mathbf{z}$를 다시 원래의 입력값 $\mathbf{x}$를 생성하도록 학습한다.	Auto Encoder는 항상 입력과 같은 벡터를 생성하도록 학습된다. 이에 확률의 개념을 도입해 출력이 함수값을 갖도록 학습하여 다양한 결과를 생성할 수 있도록 한다.
Encoder(Inference) $\qquad \hat{\mathbf{z}} = \mathbf{W}\mathbf{x}$	Encoder $\qquad \hat{\mathbf{z}} = Q_\phi(\mathbf{z} \vert \mathbf{x})$ $\qquad$($\mathbf{x}$가 주어졌을 때 $\mathbf{z}$의 확률분포) $\qquad \qquad \Downarrow$ 확률 분포에서 하나를 Sampling
Decoder(Generation) $\qquad \mathbf{x} = \mathbf{W}^{-1} \hat{\mathbf{z}}$	Decoder $\qquad \mathbf{x} = P_\theta(\mathbf{x} \vert \mathbf{z})$ $\qquad$($\mathbf{z}$가 주어졌을 때 $\mathbf{x}$의 확률분포)

VAE는 확률분포를 학습하는 만큼 기존의 Loss Function을 사용할 수 없다.
이에 ELBO(Evidence Lower Bound) 라고 불리는 Variational Lower Bound를 사용한다.

\[\text{Maximize: }\quad \mathbb{E}_{\mathbf{z} \sim Q_\phi(\mathbf{z} \vert \mathbf{x})}[log P_\theta (\mathbf{x} \vert \mathbf{z})] - \mathbb{D}_{KL}(Q_\phi(\mathbf{z} \vert \mathbf{x}) \Vert P(\mathbf{z}))\]

이제 한 항씩 살펴보자.

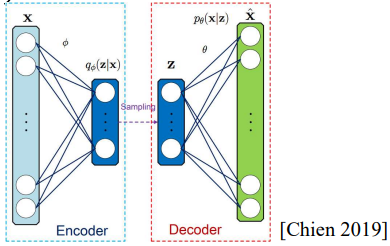
• \(\mathbb{E}_{\mathbf{z} \sim Q_\phi(\mathbf{z} \vert \mathbf{x})}[log P_\theta (\mathbf{x} \vert \mathbf{z})]\qquad \rightarrow \text{- Cross Entropy}\)
  

  $Q_\phi(\mathbf{z} \vert \mathbf{x})$, 즉 Encoder에서 Latent Vector $\mathbf{z}$를 Sampling하고
  이 $\mathbf{z}$에 대해 $\mathbf{x}$와의 -Cross Entropy(거리)를 Maximize,
  즉, $P$와 $Q$의 거리를 Minimize하는 것을 의미한다.

  • ※ Cross Entropy: $-\sum \limits_{i=1}^n q(x_i) log(p(x_i))$

• \(-\mathbb{D}_{KL}(Q_\phi(\mathbf{z} \vert \mathbf{x}) \Vert P(\mathbf{z})) \qquad \rightarrow \text{- KL Divergence}\)
  

  \(-\mathbb{D}_{KL}(Q_\phi(\mathbf{z} \vert \mathbf{x}) \Vert P(\mathbf{z})) = -\mathbb{E}_{\mathbf{z} \sim P(\mathbf{z})}[log(\frac{Q(\mathbf{z} \vert \mathbf{x})}{P(\mathbf{z})})] = - (\mathbb{E}_{\mathbf{z} \sim P(\mathbf{z})}[log(Q(\mathbf{z} \vert \mathbf{x}))] - \mathbb{E}_{\mathbf{z} \sim P(\mathbf{z})}[log(P(\mathbf{z}))])\)
  즉, $P$를 기준으로 $P$와 $Q$의 분포도 차이를 Minimize하는 것을 의미한다.

$\therefore$ 다시말해 $P$와 $Q$사이의 거리와 분포도를 비슷하게끔 만들자는 뜻이다.

---

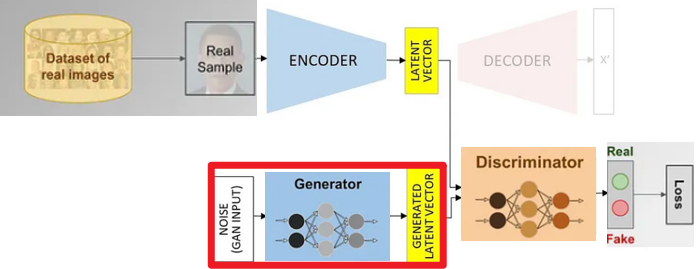
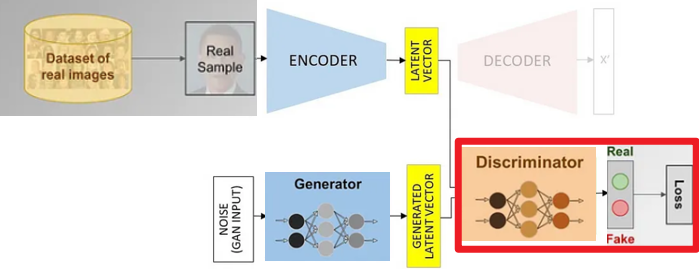
2. GAN

Generative Adversarial Network

Generator	Discriminator
Random Noise로부터 이미지를 생성한다.	Generator에서 생성된 이미지와 실제 이미지의 Latent Vector를 비교한다.

GAN은 Discriminator라는 새로운 개념을 도입한 만큼 새로운 Loss Function을 정의했다.
이 VAE와 마찬가지로 GAN Loss를 살펴보면 GAN에 대해서 이해하기 쉬울 것이다.

\[\min \limits_\theta \max \limits_\phi V(G_\theta, D_\phi) = \mathbb{E}_{\mathbf{x} \sim \mathbf{p}_{data}}[log(D_\phi(\mathbf{x}))] + \mathbb{E}_{\mathbf{z} \sim p(\mathbf{z})}[log(1-D_\phi(G_\theta(\mathbf{z})))]\]

$\theta \rightarrow \text{Generator 관련}$
$\phi \rightarrow \text{Discriminator 관련}$

이제 한 항씩 살펴보자

• \(\mathbb{E}_{\mathbf{x} \sim \mathbf{p}_{data}}[log(D_\phi(\mathbf{x}))] \qquad \rightarrow \text{- Cross Entropy}\)
  

  실제 데이터의 분포와 이 데이터를 Discriminate한 결과의 -Cross Entropy(거리)를 Maximize
  즉, 실제 데이터와 Discriminator와의 거리를 Minimize하는 것을 의미
  ($\phi$에 대해서는 Maximize 문제이므로)

• \(\mathbb{E}_{\mathbf{z} \sim p(\mathbf{z})}[log(1-D_\phi(G_\theta(\mathbf{z})))] \qquad \rightarrow \text{Cross Entropy}\)
  

  • $\phi$ 입장
    

    가짜 데이터의 Latent Vector($\mathbf{z}$) 분포와 이 데이터를 Discriminate한 결과의 Cross Entropy(거리)를 Maximize
    

  • $\theta$ 입장
    

    가짜 데이터의 Latent Vector($\mathbf{z}$) 분포에서 생성한 데이터와 이 데이터를 Discriminate한 결과의 Cross Entropy(거리)를 Minimize

$\therefore\;$ 다시말해 Discriminator는 가짜데이터를 잘 분류하도록,
$\quad$ Generator는 Discriminator가 가짜를 구분하지 못하도록 학습한다.

3. Diffusion