6. First-Order Logic

First-Order Logic

1. BackGround

propositional logic은 이 세상의 모든 문제를 Propositinoal Symbol로 나타내고 이는 오직 True/False만을 갖는다.

이 때문에 이 세상의 Object들을 표현하기에 부족한 면이 있는데, 가령 {1, 1}에 바람이 불면 주변에 함정이 있다는 사실과 {2, 2}에 바람이 불면 주변에 함정이 있다는 사실은 다르게 표현된다.

First-Order logic은 모든 문장을 Object과 Relation이 두개만으로 World를 표현하여 일반적인 상식들을 나타내기에 좋다.

1) 표현

First-Order Logic은 모든 문장을 Object과 Relation이 두개만으로 World를 표현한다.

Symbol	First-Order Logic	Propositional Logic
Constant Symbol	Object 　: 그 자체로 정의되어 있는 것 　(ex. 괴물, 금, John)
Predicate Symbol (서술)	Relation 　: True, False를 판단할 수 있는 것 　(ex. love(x), under(x), ….)	$\sim$ Proposition Symbol 　: True, False를 판단할 수 있는 Symbol 　(ex. P, Q, R)
Function Symbol	함수 　: output의 결과가 Object인 것 　(ex. Mother(x))

이 Symbol들과 변수는 아래의 Term(인자, argument)들과 같이 문장을 구성한다.

Ground Term	$John, Mother(John)$과 같이 Variable이 없는 문장
Complex Term	함수를 이용한 Term (Mother(John), Mother(Mother(Jon))과 같은 문장은 Ground Term이면서 Complex Term이다)
Atomic Sentence	Predicate가 반드시 하나 이상 있는 문장
Complex Sentence	논리 접속사들을 사용해서 Atomic Sentence를 연결한 문장

---

Model

PL과는 다르게 First Order Logic에서는 Truth Table을 그릴 수 없다. 즉, Truth Table의 한 행이었던 Model을 다시 정의해야 한다.

FL에서 Model은 Vocabulary와 Object의 Mapping을 의미한다. 이 그림에서는 2개의 Constant Symbol이 있고, Object는 총 5개이다. (Person, Person_king, leftleg(Person), leftleg(Person_king), Crown) 즉, Constant Symbol을 Object에 연결하는데에만 $5^2$개의 Model이 생긴다. (실제 모든 경우의 수를 다 계산하면 137506194466개 이다)

---

Quantifier

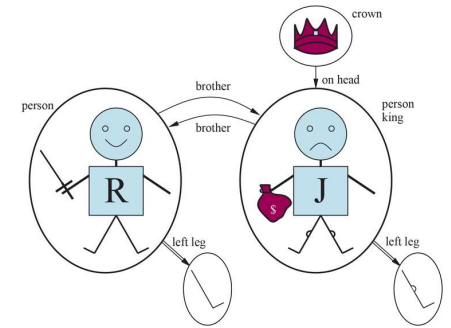
$\forall x$	모든 x에 대해 문장이 True여야 함	”$\Rightarrow$”와 잘어울린다. $\forall x King(x) \Rightarrow Person(x)$ ($x$가 King이 아니면 $King(x)$는 False이지만 Implication에 의해 전체 문장은 True가 되기 때문 만약 $\wedge$를 썼으면 전체문장은 False이다.)
$\exists x$	어떤 x에 대해 True인게 하나만 있으면 됨	”$\wedge$”와 잘어울린다. $\exists x Crown(x) \wedge onHead(x, John)$ (x가 Crown이 아니어도, 이미 만족하는 경우가 하나 존재하기 때문 만약 $\Rightarrow$를 썼으면 전체문장은 False이다.)
$\neg$	드모르간 법칙 ⅰ. $\neg \forall x \neg Loves(x, A) \equiv \exists x Loves(x, A)$ ⅱ. $\neg \exists x \neg Loves(x, A) \equiv \forall x Loves(x, A)$

Rule

Propositional Logic과 First-Order Logic의 다른점은 변수뿐이다.
즉, 이 변수를 없애주면 Propositinal Logic을 적용할 수 있다.

Propositionalization

1. Universal Instantiation
   

   FOL문장에서 $\forall$이 포함된 변수는 Ground Term으로 치환가능하다.

2. Existential Instantiation
   

   FOL문장에서 $\exists$가 포함된 변수는 KB에 한번도 쓰이지 않은 Constant Symbol로 치환가능하다.

먼저 위 두가지 규칙을 통해 변수와 Quantifier를 없앨 수 있다.

만약 sentence가 FOL에 의해 KB에 Entail된다면 Complete 알고리즘이다.
(x, f(x)에서 f(f(x))이렇게 무한하게 늘어날 수 있다.)