포스트

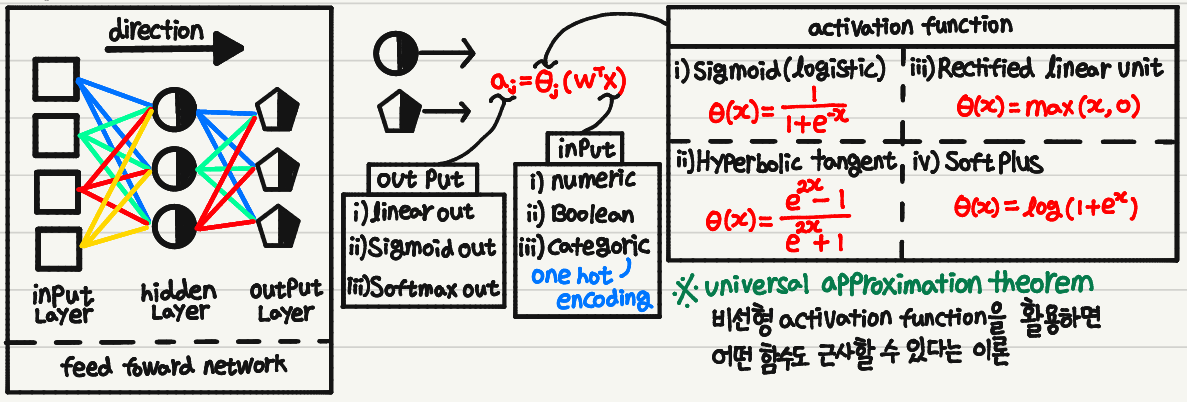
1. Feedfoward Neural Network

게시 업데이트
By UI-JIN KIM 12 분읽는 시간

Feedfoward Neural Network

1. 구조

alt text

2. Train

1) Loss Function

종류

대표적인 Loss Function들에는 다음이 있다.

Squared ErrorNegative Log LikelihoodCross Entropy
$L(\mathbf{y}, h_w(\mathbf{x})) = \sum \limits_{i=1}^n (y_i - \hat{y}_i)^2$$L(\mathbf{y}, h_w(\mathbf{x})) = - log (P_w(\mathbf{y} \vert \mathbf{x}))$\(\mathbb{H}(P, Q) = - \mathbb{E}_{\mathbf{z \sim P(\mathbf{z})}}[log(Q(\mathbf{z}))] \\ \qquad \quad \;\; = - \int P(\mathbf{z}) log(Q(\mathbf{z})) \\ \mathbb{H}(\mathbf{y}, \hat{\mathbf{y}}) = - \sum \limits_i y_i log(\hat{y}_i)\)
예측값과 정답사이의 L2-Norm입출력 관계를 얼마나 잘 설명하는지P의 분포와 Q의 분포사이의 거리

Minimization

  • 직접 계산
    $\mathbf{W}^* = \text{arg}\min \limits_\mathbf{W} \sum \limits_{\mathbf{x, y} \in \mathcal{D}} L(\mathbf{y}, \mathbf{h}_\mathbf{W}(\mathbf{x}))$
  • Gradient Descent
    $\mathbf{W} = \mathbf{W} - \alpha \nabla \text{Loss}(\mathbf{W})$

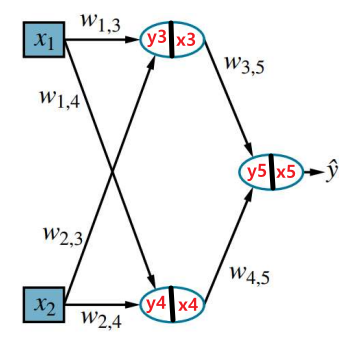
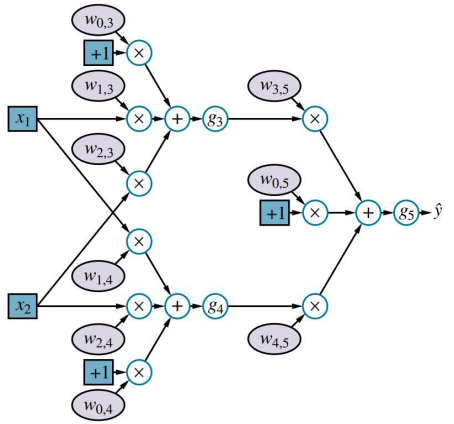
2) Backpropagation

그렇다면 각 Layer마다 Loss의 Gradient는 어떻게 구할 수 있을까??

alt text
$\text{Loss}(\mathbf{W}) = L_2(y, h_\mathbf{W}(\mathbf{x})) = (y-\hat{y})^2$
$\text{act}(y) = \text{Sigmoid}(y) = \frac{1}{1+e^{-y}}$		ⅰ. $w_{3, 5}$의 Gradient 계산 $\rightarrow \frac{\partial \text{Loss}(\mathbf{W})}{\partial w_{3, 5}}$
$\quad$ ※ $y_5 = \text{bias} + x_3w_{3, 5} + x_4w_{4, 5}$
$\quad$ ※ $\hat{y} = x_5 = \text{act}(y_5)$

\(\frac{\partial \text{Loss}(\mathbf{W})}{\partial w_{3, 5}} \\ = \frac{\partial (y-\hat{y})^2}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial w_{3, 5}} \\ = \frac{\partial (y-\hat{y})^2}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial y_5} \times \frac{\partial y_5}{\partial w_{3, 5}} \\ = -2(y-\hat{y}) \times \hat{y}' \times x_3 \\ = \;\vartriangle_5 \times x_3\)

ⅱ. $w_{1, 3}$의 Gradient계산 $\rightarrow \frac{\partial Loss(W)}{\partial w_{1, 3}}$
$\quad$※ $y_5 = \text{bias} + x_3w_{3, 5} + x_4w_{4, 5}$
$\quad$※ $y_3 = \text{bias} + x_1 w_{1, 3} + x_2 w_{2, 3}$
$\quad$※ $\hat{y} = x_5 = \text{act}(y_5)$
$\quad$※ $x_3 = \text{act}(y_3)$

\(\frac{\partial \text{Loss}(\mathbf{W})}{\partial w_{1, 3}} \\ = \frac{\partial (y-\hat{y})^2}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial w_{1, 3}} \\ = \frac{\partial (y-\hat{y})^2}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial y_5} \times \frac{\partial y_5}{\partial x_3} \times \frac{\partial x_3}{\partial y_3} \times \frac{\partial y_3}{w_{1, 3}} \\ = -2(y-\hat{y}) \times \hat{y}' \times w_{3, 5} \times \hat{y}' \times x_1 \\ =\; \vartriangle_3 \times x_1\)

위의 계산과정을 보면 알 수 있듯이 층마다 Gradient가 계속 곱해지는 것을 알 수 있다.

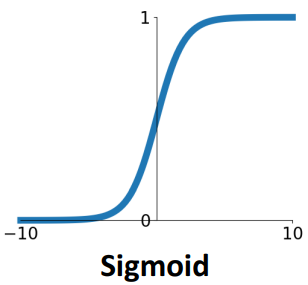
이때, Sigmoid같은 경우는 미분값이 최대 0.25기 때문에 깊은 층일수록 Gradient의 변화가 매우 작아질 수 밖에 없음을 알 수 있다.
이러한 현상을 Gradient Vanishing현상이라고 한다.

방지 대책

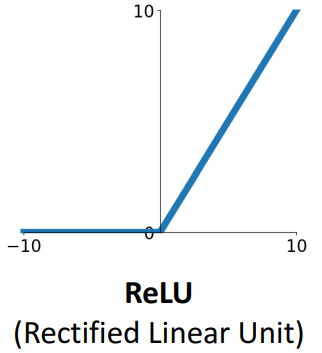
  • ReLU
    Gradient가 1이 되도록 하여 깊은 층에서도 작아지지 않게 하는 방법
    • 단점: 층이 깊어질 수록 입력값이 0이되는 경우가 많아져 Dying ReLU현상이 발생한다.
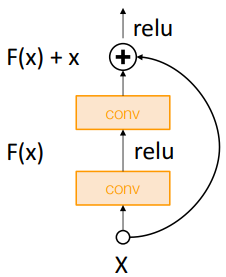
  • Skip Connection
    별도의 Connection을 통해 깊은 층에서도 Gradient를 유지하는 방법

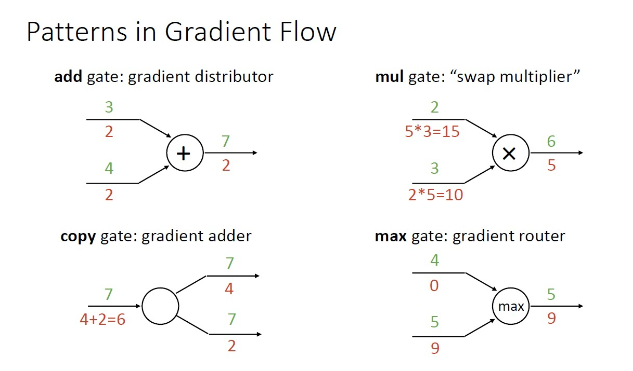
Gradient Flow

alt textalt text

Backpropagation을 Graph로 정리해보면 위와 같다.

3) Optimization

SGD

Algorithm

alt text

장점

  • Stochasticity를 유지할 수 있다. (Local Minimum 탈출 가능)
  • Parallelism하게 동작할 수 있다.

3. Generalization

복잡한 가설에는 Penalty를 주는 방법

1) Weight Decay

$\text{arg} \min \limits_\mathbf{W}(\sum \limits_{(x, y)}L(\mathbf{y}, h_\mathbf{W}(\mathbf{x}))+ \lambda \sum \limits_{i, j} W_{i, j}^2)$

alt text

Weight Decay는 MAP로써도 해석할 수 있다.

2) Drop Out

몇몇 노드를 일정 확률로 비활성화하여 각 노드들이 더 많은 정보를 학습할 수 있도록 하는 것

  • 매 학습마다 다른 구조의 모델이 학습되는데 때문에 Ensemble(Bagging)의 효과를 얻을 수 있다는 해석도 존재

※ Drop Connect: Node가 아닌 Weight를 Drop하는 방법

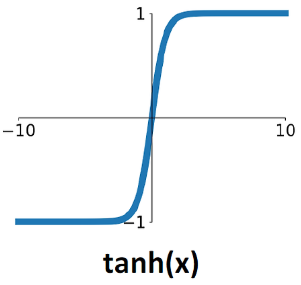
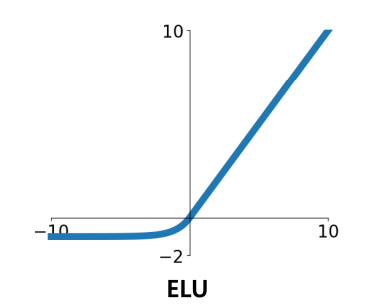
4. Activation Function

Activation Function장점단점
alt text
\(\sigma(x) = \frac{1}{1+e^{-x}}\)		- 입력 값을 [0, 1]로 압축
- 출력을 확률로 해석 가능		- Saturated Gradient
- Not Zero centered output
- Computationally Expensive
alt text- Zero centered output- Saturated Gradient
- Computationally Expensive
alt text
\(\sigma(x) = \max(0, x)\)		- Computationally Efficient
- Converge속도가 빠름		- Not Zero centered output
- Saturated Gradient ($if < 0$)
- 0에서 미분 불가능
alt text
$\sigma(x) = \max(0.01x, x)$		- Computationally Efficient
- Converge속도가 빠름
- Not saturated gradient		- 하이퍼 파라미터가 존재
- 0에서 미분 불가능

※ PReLU
$\sigma(x) = \max(\alpha x, x)$
$\rightarrow$ learnable parameter도입
alt text
\(\sigma(x) = \begin{cases}x & \text{if. } x > 0 \\ \alpha(e^x - 1) & \text{if. } x \leq 0\end{cases}\)		- 0에서 미분 가능
- Zero centered output
- Converge속도가 빠름
- Not saturated gradient

※ 변형된 버전으로 자동으로
normalize효과를 주는
SELU 활성화 함수도 있다.		- Computationally Expensive

※ 활성화 함수는 단조 증가의 형태를 갖게 되는데, 이 이유는 활성화 함수가 단조 증가/감소가 아닐 경우 여러 Output을 가질 수 있고, 이는 Input의 정보를 파괴할 수 있기 때문이다.

하지만 GELU에서는 단조 증가/감소함수가 아닌데, 이 이유에 대해서는 논문에 자세히 나와있다. (Normalize와 관련된 내용인듯?)

위의 Activation Function의 핵심은 다음을 고려해야 한다는 것 같다.

ⅰ) Gradient가 0으로 Saturated되는 부분을 줄여야 한다.

만약 Gradient가 0, 혹은 0에 매우 가까울 경운 경우가 많다면 이는 Shallow network에서는 상관 없을 수는 있지만 Deep network에서는 backpropagation되는 gradient가 점점 작아져 input에 가까운 neuron은 정보를 전달받지 못하게 된다.

ⅱ) Output이 Zero Center를 가져야 한다.

이 점은 대부분의 딥러닝 process가 mini-batch를 사용하기 때문에 큰 영향이 없을 수 있다. 하지만 이론적으로 알아두면 좋을 것 같다.

핵심은 Zero Center가 아닌 경우, 즉 Output이 항상 양수이거나 음수인 경우에는 모든 Weight의 Gradient가 같은 부호를 갖는다는 것이다. Backpropagation의 경우 $\frac{\partial \mathcal{L}}{\partial W} = \frac{\partial \mathcal{L}}{\partial z} \times \frac{\partial z}{\partial W}$와 같이 Chain rule을 사용한다. 예를들어 Sigmoid의 경우 위 식은 $\sigma(z)(1-\sigma(z))(y_{pred} - y_{true})$와 같이 나타낼 수 있는데, $\sigma(z)(1-\sigma(z))$는 항상 양수가 되므로 $\frac{\partial \mathcal{L}}{\partial W}$는 $y_{pred} - y_{true}$와 부호가 같다는 것을 알 수 있다. 즉 sample이 1개일 때는 모든 weight가 같은 방향으로 update가 되고 결국 optimal weight까지 지그재그로 갈수밖에 없다. (하지만 batch의 경우 각각의 sample에 의해 부호가 결국 달라진다.)

※ Model의 입력 전, Data processing과정 중 input이 zero center를 갖도록 Normalize해주는 이유도 이와 같은 이유이다.

ⅲ) 적은 연산량을 가져야 한다.

Exponential함수는 연산량이 많아진다.

ⅳ) 미분 가능해야 한다.

5. Weight Initialization

Weight를 초기화 하는 방법에 대해 알아보기 전에 먼저 다음의 경우를 생각해 보아야 한다.

Weight와 Bias가 0인 경우Weight와 Bias가 c인 경우
레이어의 입력과 별개로 출력은 항상 0이다.
Chain rule에 의해 Gradient도 항상 0이다.		모든 Gradient가 동일한 값을 갖는다.

즉 위와 같이 초기화 하는 경우 학습시작할 수 없게된다.

Weight Initialization의 목적은 모델이 Global Minimum을 갖도록 하기 위해 사용하는 것이 아니다. 모델이 학습을 잘 시작하게끔 하는 것이 목적이다. 이를 위해서는 모든 Weight가 Gradient를 갖게끔 하는 것이 중요하다.

1) Random Initialization

alt text

1

W = 0.01 * np.random.randn(Din, Dout)

ⅰ) 평균은 0 표준편차는 0.01인 매우 작은 값으로 가우시안 분포로 초기화 하는 방법

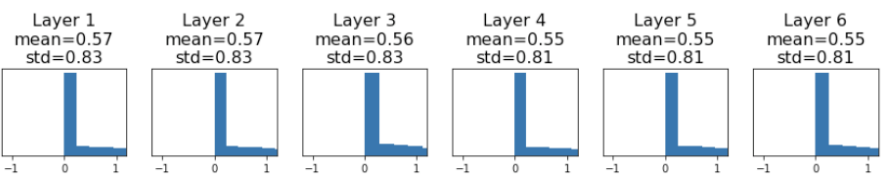
이 경우 Shallow network에서는 잘 동작하지만 Deep network에서는 잘 동작하지 않는다. 위의 그림을 보면 알 수 있듯이 layer를 지날수록 Weight들의 분산은 점점 작아지게 되기 때문이다.

(※ 위의 예시는 tanh를 활성화 함수로 정했을 때의 예시이다.)

alt text

1

W = 0.05 * np.random.randn(Din, Dout)

ⅱ) 평균은 0 표준편차는 0.05로 표준편차를 더 키워 초기화 하는 방법

위와 마찬가지로 Shallow network에서는 잘 동작하지만 Deep network에서는 잘 동작하지 않는다. 활성화 함수로 어떤 것을 사용하는지에 따라 달라지겠지만 tanh를 예시로 들 경우 위의 그림처럼 layer를 지날수록 이번에는 점점 모든 값들이 1또는 -1로 모이게 되기 때문이다.

2) Xavier Initialization

alt text

1

W = (1 / np.sqrt(Din)) * np.random.randn(Din, Dout)

ⅰ) Layer의 입력과 출력의 분산이 동일하도록 설정하는 방법

위의 문제들은 대부분 입력과 출력의 분산이 달라진다는 것이 문제가 되었다. 따라서 다음과 같은 식을 활용할 수 있다.

\[y = Wx \\ y_i = \sum^{Din}_{j=1}x_jw_j \\ \text{var}(y_i) = \text{Din} \times \text{var}(x_iw_i) = \text{Din} \times \text{var}(x_i) \times \text{var}(w_i)\]

즉, $\text{var}(w_i) = \frac{1}{\text{Din}}$일 경우 입력과 출력의 분산은 같아진다는 것을 알 수 있다.

※ CNN의 경우 $\text{Din} = \text{Input channels} \times \text{kenel size}^2$

alt text

하지만 Xavier Initialization도 활성화 함수로 Tanh가 아니라 ReLU를 사용하면 위와 같은 형태를 보이게 된다는 문제점이 있다.

3) Kaiming Initialization

alt text

1

W = (2 / np.sqrt(Din)) * np.random.randn(Din, Dout)

ⅰ) 출력의 분산을 입력의 2배로 설정하는 방법

Xavier를 ReLU와 함께 사용할 때 발생하는 문제점을 해결하기 위해 단순히 분산을 늘려준 구조를 말한다. 이를 통해 0에 모여있던 값들을 더 고르게 분포하도록 만들 수 있다.

 ※ Skip connection에서의 initialization
alt textCNN에서 주로 사용하는 Residual Network에서는
$\text{Var}(F(x) + x) > \text{Var}(x)$이기 때문에
kaiming initialization을 사용하면 분산이 계속 증가한다.
따라서 2번째 conv layer의 값은 모두 0으로 초기화 해야 한다.
이 경우 $\text{Var}(F(x) + x) = \text{Var}(x)$가 성립한다.
Artificial Intelligence, Deep Learning(Basic)
ai
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.