3. Eigenvalues
Eigenvalues
1. 고윳값 분해(EigenValue Decomposition)
1) 고윳값, 고유벡터
$A\mathbb{x} = \lambda \mathbb{x}$
※ $A$: 행렬, $\mathbb{x}$: 0이 아닌 벡터, $\lambda$: 스칼라
- $\mathbb{x}$ = 고유 벡터
- $\lambda$ = 고유값
0이 아닌 어떤 벡터 $\mathbb{x}$에 대해 행렬 A에 의한 선형 변환의 결과가 자기 자신의 상수배가 될 때(즉, 방향이 변하지 않을 때) 상수값과 벡터를 말한다.
고유값
$(\lambda - A) \mathbb{x} = 0$이 $\mathbb{x} \neq 0$인 해(자명하지 않은 해)를 가져야 한다.
만약 $(A-\lambda I)$의 역행렬이 존재한다고 하면 $\mathbb{x}=0$만을 해로 가지기 때문에 처음 가정과 모순이다.따라서 특성방정식 $det(\lambda I - A) = 0$ 을 만족하는 λ가 고유값이다.
또, 이 고윳값으로 대각합과 행렬식을 구할 수 있다,
- $det(A) = \prod \limits_{i=1}^N \lambda_i$
- $tr(A) = \sum \limits_{i=1}^N \lambda_i$
고유벡터
고유값 λ 를 먼저 구한 후,
$(\lambda - A) \mathbb{x} = 0$에 대입하여 $\mathbb{x}$를 구한다.
2) 대각화
어떤 행렬 $A$의 고유값과 고유벡터를 알아내면 대각화를 쉽게 할 수 있다.
즉, 이로써 계산상의 이점을 얻을 수 있다.대각화가능성 및 대각화
고유값과 고유벡터로 부터 행렬얼 어떻게 대각화 할 수 있는지 알아보자.
ⅰ. 행렬 A의 고유값과 고유벡터가 각각 $(\lambda_1, \lambda_2, … , \lambda_n), \quad (\mathbf{v}_1, \mathbf{v}_2, …, \mathbf{v}_n)$ 이라고 하자.
ⅱ. 고유값과 고유벡터의 정의에 의해 다음과 같이 쓸 수 있다.
\(\begin{pmatrix} \mathbf{Av}_1 = \lambda_1 \mathbf{v}_1\\ \mathbf{Av}_2 = \lambda_2 \mathbf{v}_2\\ \vdots \\ \mathbf{Av}_n = \lambda_n \mathbf{v}_n \end{pmatrix} \rightarrow \mathbf{A} \begin{pmatrix} \mathbf{v}_1\\ \mathbf{v}_2\\ \vdots \\ \mathbf{v}_n \end{pmatrix}^T = \begin{pmatrix} \mathbf{v}_1\\ \mathbf{v}_2\\ \vdots \\ \mathbf{v}_n \end{pmatrix}^T \begin{pmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \lambda_n \end{pmatrix}\)
($\mathbf{v}_i$는 열벡터임을 주의)ⅲ. 이때, $P = \begin{pmatrix} \mathbf{v}_1 & \mathbf{v}_2 & … & \mathbf{v}_n \end{pmatrix}$ 의 역행렬이 존재하기 위해서는 원소들이 선형 독립이어야 한다.
ⅳ. 만약 $P$의 역행렬이 존재한다고 하면 다음과 같이 쓸 수 있다. \(\mathbf{A} \mathbf{P} = \mathbf{P} \mathbf{\Lambda} \rightarrow \mathbf{A} = \mathbf{P} \mathbf{\Lambda} \mathbf{P}^{-1} \\ \&\quad \mathbf{P} = \begin{pmatrix} \mathbf{v}_1 & \mathbf{v}_2 & ... & \mathbf{v}_n \end{pmatrix} \\ \&\quad \mathbf{\Lambda} = \begin{pmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \lambda_n \end{pmatrix}\)
활용
이 대각화의 결과($A = P^{-1} D P$)는 닮음과도 관련이 있다.
$\rightarrow$ 닮음: $AP = PB$, 즉 두 정사각행렬이 같은 선형 변환의 서로 다른 기저에 대한 표현임을 나타내는 관계행렬 A를 대각화하면 다음과 같은 식을 활용할 수도 있다.
$A^n = (P^{-1} \Lambda P) … (P^{-1} \Lambda P) = (P^{-1} \Lambda^n P)$
3) 직교대각화
\[A = \mathbf{U \Lambda U}^T = \begin{pmatrix}u_1 & u_2 & ... & u_n\end{pmatrix} \begin{pmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \lambda_n \end{pmatrix} \begin{pmatrix} u_1^T \\ u_2^T \\ \vdots \\ u_N^T \end{pmatrix} \\\]
- 직교대각화란 고유벡터($\mathbf{U} = \begin{bmatrix}\mathbf{u}_1 & \mathbf{u}_2 & … & \mathbf{u}_n \end{bmatrix}$)들이 모두 직교 한다는 뜻이다.
ⅰ. $(if \; i\neq j) \qquad \mathbf{u}_i^T\mathbf{u}_j = 0$
ⅱ. $(if \; i=j) \qquad \mathbf{u}_i^T\mathbf{u}_j = 1$직교행렬의 성질
$Q^TQ = QQ^T = I \quad \rightarrow Q^{-1} = Q^T$
$Q^T$또한 직교행렬이다.
직교행렬 $Q$에 의한 곱셈변환은 길이가 보존된다.(내적보존)
$\Vert Q\mathbf{x} \Vert = (Q\mathbf{x})^TQ\mathbf{x} = \mathbf{x}^TQ^TQ\mathbf{x} = \mathbf{x}^T\mathbf{x} = \Vert \mathbf{x} \Vert$대칭행렬($A^T=A$)의 성질
고유값이 항상 실수이다.
고유벡터는 모두 직교한다.
$\rightarrow $ 대칭행렬의 대각화와 직교대각화는 동치동치인 명제들
ⅰ. 만약 PSD (Positive Semi Definite)이면 $\rightleftarrows$ 모든 고유값 $\lambda_i \geq 0$
ⅱ. 만약 PD (Positive Definite)이면 $\rightleftarrows$ 모든 고유값 $\lambda_i > 0$
ⅲ. 역행렬이 존재한다 $\rightleftarrows$ 모든 고유값 $\lambda_i \neq 0$
$\rightarrow \quad A^{-1}=\mathbf{U} \Lambda^{-1} \mathbf{U}^T$
\(\qquad \Lambda^{-1} = \begin{pmatrix} \frac{1}{\lambda_1} & 0 & ... & 0 \\ 0 & \frac{1}{\lambda_2} & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \frac{1}{\lambda_n} \end{pmatrix}\)직교대각화
$A$가 대칭행렬이라면, 대각화시 직교대각화를 할 수 있고,
$A = \mathbf{U \Lambda U}^T$ 이다.
Rank-1 matrix 분해
\(A = \mathbf{U \Lambda U}^T = \begin{pmatrix}u_1 & u_2 & ... & u_n\end{pmatrix} \begin{pmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \lambda_n \end{pmatrix} \begin{pmatrix} u_1^T \\ u_2^T \\ \vdots \\ u_N^T \end{pmatrix} \\ = \begin{pmatrix} \lambda_1 u_1 & \lambda_2 u_2 ... \lambda_n u_n\end{pmatrix} \begin{pmatrix} u_1^T \\ u_2^T \\ \vdots \\ u_N^T \end{pmatrix} \\ = \sum \limits_{i=1}^n \lambda_i u_i u_i^T\)
$\rightarrow$ 즉, $\lambda_i$ 는 단위벡터 $u_i$ 방향에 대한 Gain으로 생각할 수 있다.Ellisoid(타원체) = $\begin{Bmatrix} \mathbf{x} | \mathbf{x}^T Q \mathbf{x} \leq 1 \end{Bmatrix}$
\(\mathbf{x}^T Q \mathbf{x} = \sum \limits_i \lambda_i \hat{x}_i^2 = \sum \limits_i \frac{\hat{x}_i^2}{(\frac{1}{\sqrt{\lambda_i}})^2} \leq 1\)
$\because$ Positive Definite이 대칭행렬이므로 $\lambda_i =(\frac{1}{\sqrt{\lambda_i}})^2$PSD인 경우 $Q=I$이면 Norm으로 사용 가능하다.
2. Quadratic Form
1) 정의
Linear Form
$f(\mathbf{x}) = \mathbf{a}^T\mathbf{x}$(a는 벡터)
$= a_1x_1 + a_2x_2 + … + a_nx_n$1차항으로만 이루어진 x벡터와의 선형결합을 나타내는 식
Bilinear Form
$f(\mathbf{x, y}) = \mathbf{x}^TA\mathbf{y}$(A는 행렬)
$ = a_{11}x_1y_1 + a_{21}x_2y_1 + … + a_{mn}x_my_n$1차항으로 이루어진 2개의 벡터 x,y의 선형결합으로 이루어진 식
Quadratic Form
$f(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} = \sum_{i=1}^n \sum_{j=1}^n q_{ij} \mathbf{x}_i \mathbf{x}_j$(A는 행렬)
$ = a_{11}x_1x_1 + a_{21}x_2x_1 + … + a_{mn}x_mx_n$Bilinear Form에서 $y=x$인 Special Form으로 벡터 x의 linear function($f: \mathbb{R}^n \rightarrow \mathbb{R}$)을 의미하는 식
(2차함수의 Vector버전을 나타냄)Symmetric
우리는 행렬 $A$는 항상 Symmetic행렬일 것으로 가정할 것이다.
이는 다음과 같이 Quadratic Form에서는 항상 A를 Symmetric행렬로 바꿀 수 있기 때문이다.ⅰ. 우선 $f(x)$의 결과는 Scalar이기 때문에 항상 $f(x) = f(x)^T$이다.
ⅱ. 즉, $\mathbf{x}^TA\mathbf{x} = (\mathbf{x}^TA\mathbf{x})^T = \mathbf{x}^TA^T\mathbf{x}$ 이다.
ⅲ. 따라서 다음과 같이 같은 $A$와 결과를 내는 Symmetric행렬을 만들 수 있다.
\(\therefore f(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} = \frac{\mathbf{x}^TA\mathbf{x}}{2} + \frac{\mathbf{x}^TA\mathbf{x}}{2} = \frac{\mathbf{x}^TA\mathbf{x}}{2} + \frac{\mathbf{x}^TA^T\mathbf{x}}{2} = \mathbf{x}^T \frac{(A+A^T)}{2} \mathbf{x}\)
2) PSD, PD
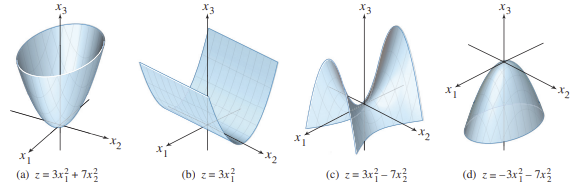
Quadratic Form이 가질 수 있는 형태는 다음 5가지와 같다.
- ⅰ. Positive Definite(밑으로 볼록)
- $\mathbf{x} = \begin{Bmatrix}0, …, 0\end{Bmatrix}$인 점을 제외한 모든 $\mathbf{x} \in \mathbb{R}^n$에 대해 $\mathbf{x}^TQ\mathbf{x}>0$이 성립하는 $Q$
- ⅱ. Positive Semidefinite(밑으로 볼록)
- 모든 $\mathbf{x} \in \mathbb{R}^n$에 대해 $\mathbf{x}^TQ\mathbf{x} \geq 0$이 성립하는 $Q$
- ⅲ. Negative Defineite(위로 볼록)
- $\mathbf{x} = \begin{Bmatrix}0, …, 0\end{Bmatrix}$인 점을 제외한 모든 $\mathbf{x} \in \mathbb{R}^n$에 대해 $\mathbf{x}^TQ\mathbf{x}>0$이 성립하는 $Q$
- ⅳ. Negative Semidefinite(위로 볼록)
- 모든 $\mathbf{x} \in \mathbb{R}^n$에 대해 $\mathbf{x}^TQ\mathbf{x} \geq 0$이 성립하는 $Q$
- ⅴ. Indefinite(위로 볼록 + 아래로 볼록)
- 위의 그림에서 “(c)”와 같이 자르는 단면 $\mathbf{x}$에 따라 위로볼록과 아래로볼록이 달라지는 형태의 $Q$
$\rightarrow$ 즉, 최대 최소가 존재하지 않는다.
$\rightarrow \mathbf{x}^TA\mathbf{x}$는 $\infty$와 $-\infty$로 모두 발산한다.모양 판별
- 위에서 살펴보았듯이 $f(\mathbf{x}) = \mathbf{x}^TA\mathbf{x}$에서 A는 항상 Symmetric Matrix로 가정할 수 있다.
- $\therefore A = U \Lambda U^T$
- 즉, $f(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} = \mathbf{x}^T ( U \Lambda U^T ) \mathbf{x} = y^T \Lambda y$
\(y = U^T \mathbf{x} \\ \Lambda = \begin{pmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & ... & \lambda_n \end{pmatrix}\)따라서, $\mathbf{x}^TA\mathbf{x} = \sum_{i=1}^n \sum_{j=1}^n q_{ij} \mathbf{x}_i \mathbf{x}_j$ 이므로
$\therefore f(\mathbf{x})=y^T \Lambda y=\sum \limits_i \lambda_i y_i^2$ⅰ. 만약 PSD (Positive Semi Definite)이면 $\rightleftarrows A$의 모든 고유값 $\lambda_i \geq 0$
ⅱ. 만약 PD (Positive Definite)이면 $\rightleftarrows A$의 모든 고유값 $\lambda_i > 0$
ⅲ. 만약 Indefinite이면 $\rightleftarrows A$의 고유값이 양수와 음수를 모두 가짐
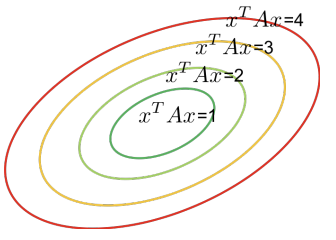
3) Ellipse
위의 내용들에 따라 Quadratic Form은 항상 다음과 같은 형태를 갖는다.
$f(\mathbf{x})=\mathbf{x}^TA\mathbf{x} = y^T \Lambda y=\sum_i \lambda_i y_i^2$
※ $y=U^T \mathbf{x}$, $\quad U$는 A의 EigenVector, $\quad \Lambda$는 A의 EigenValues이때, f가 PSD인 Quadratic Form이고, 항상 c를 지난다고 하면
$f(\mathbf{x})=y^T \Lambda y=\sum \limits_i \lambda_i y_i^2 = \sum \limits_i \frac{y_i^2}{(\sqrt{\frac{1}{\lambda_i}})^2} = c$즉, 다음을 만족하는 타원의 방정식으로 변형할 수 있다.
- 좌표계(기저벡터): $\begin{pmatrix}y_1 & y_2 & … & y_n \end{pmatrix}$
- 축의 길이: $\begin{pmatrix}\frac{1}{\sqrt{\lambda_1}} & \frac{1}{\sqrt{\lambda_2}} & … & \frac{1}{\sqrt{\lambda_n}} \end{pmatrix}$
※ 큰 Eigenvalue를 갖는 방향이 더 짧은 축에 해당된다.
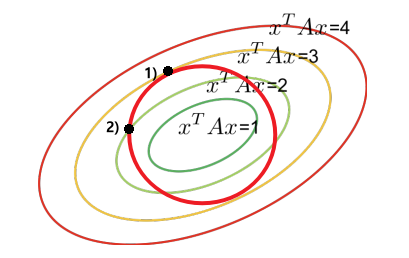
Rayleigh Quotient
Rayleigh Quotient란?
$A$가 PSD일 때, $R(A, \mathbf{x}) = \frac{\mathbf{x}^T A \mathbf{x}}{\mathbf{x}^T\mathbf{x}}$Maximize $R(A, \mathbf{x})$?
ⅰ. $\mathbf{x}^T \mathbf{x}$는 원이다$(= \mathbf{x}^T I \mathbf{x})$
ⅱ. $\mathbf{x}^T A \mathbf{x}$는 타원이다.
$\rightarrow$ 즉, $\mathbf{x}^T \mathbf{x}$가 어떤 방향을 가리켜야 타원이 최대가 되는지 찾는 문제이다.위의 그림에서 1번점과 2번점을 살펴보자.
1번점은 $\mathbf{x}^T A \mathbf{x}=3$인 점을 지나고 2번점은 $\mathbf{x}^T A \mathbf{x}=2$인 점을 지난다.즉, 원이 $\mathbf{x}^T A \mathbf{x}$의 단축방향 일수록(Eigenvalue $\lambda$ 가 클수록) 더 큰 값을 갖게 된다.
- 수식적 증명
$\begin{pmatrix}\frac{\lambda_{min} \sum_{i=1}^n y_i^2}{\sum_{i=1}^n y_i^2} = \lambda_{min} \end{pmatrix} \leq \frac{\mathbf{x}^T A \mathbf{x}}{\mathbf{x}^T\mathbf{x}} = \frac{\sum_{i=0}^n \lambda_i y_i^2}{\sum_{i=0}^n y_i^2} \leq \begin{pmatrix} \frac{\lambda_{max} \sum_{i=1}^n y_i^2}{\sum_{i=1}^n y_i^2} = \lambda_{max} \end{pmatrix}$
3. 특이값 분해(Singular Value Decomposition)
사용분야: 알고리즘, 자료압축
1) 특이값
고유값은 정방행렬에서만 정의 되었기 때문에, 정방행렬이 아닌 $A_{M \times N}$행렬에서는 정방행렬과 같은 방법으로는 대각행렬을 찾을 수 없다.
$A^TA$의 성질
1. Symmetric Matrics이다 2. Positive Semidefinite하다. 증명 $(A^TA)^T = A^T(A^T)^T = A^TA$ $\mathbf{x}^T \;A^TA \;\mathbf{x} = (A\mathbf{x})^T A\mathbf{x} = \Vert A\mathbf{x} \Vert^2 \geq 0$ 특징 ⅰ. Square Matrix이다
ⅱ. 고유값이 항상 실수이다.
ⅲ. 고유벡터가 모두 직교한다.
(직교대각화가 가능)ⅰ. $A^TA$의 모든 고유값 $\lambda_i \geq 0$
ⅱ. Scalar의 $x^2$와 같은 역할을 한다$(f: \mathbb{R}^n \rightarrow \mathbb{R} \geq 0)$
$\rightarrow$ 참고: 행렬의 $A^2$은 PSD를 보장하지 않는다.
$\rightarrow$단, A가 Symmetric일 경우는 제외
ⅲ. 만약 모든 Column이 선형 독립이면 Positive Definite이다.특이값
$A^TA$의 고유값을 $\lambda_1, \lambda_2, …, \lambda_n$이라고 할 때,
$\sigma_1 = \sqrt{\lambda_1},$
$\sigma_2 = \sqrt{\lambda_2},$
…
$\sigma_n = \sqrt{\lambda_n}$
을 행렬 $A$의 특이값이라고 한다.특이행렬
2) 특이값 분해
대각화: $A = P^{-1} D P$ (단, A는 정방행렬)
직교대각화: $A = U\sum V^T$ (단, A는 $M \times N$의 행렬)
대각화
대각화는 정방행렬 $A와$ 닮음,
즉 $A= P^{-1} D P$를 만족하는 대각행렬을 찾는 문제였다.
- $D$
- $A$의 고유값들로 이루어진 대각행렬
- $P$
- $D$의 고유값에 대응하는 열벡터 $\vec{p}$들로 이루어진 행렬
직교 대각화
직교대각화는 $A$와 직교적으로 닮음,
즉, $A = P^{T} D P$를 만족하는 대각행렬을 찾는 문제이다.이때, 위 식은 $A = U\sum V^T$로 분해할 수 있다.
- $\sum$
- $A$의 특이값이 주대각에 있고 나머지 원소가 0인 $M \times N$행렬
- $\sigma_1 > \sigma_2 > … > \sigma_n$을 만족하도록 배열되어 있음
- $V^T$
- $\sum$의 각 특이값에 대응하는 고유열벡터 $V={\vec{v_1}, \vec{v_2}, …, \vec{v_n}}$의 전치행렬
※ $AV = US$
Rank-r 근사
행렬 A에 대해 특이값 분해를 수행하여 $A = U\sum V^T$를 얻었을 때, 열 행 전개를 이용하면
$A = \sigma_1 \vec{u_1} {v_1}^T + \sigma_2 \vec{u_2} {v_2}^T + … + \sigma_n \vec{u_n} {v_n}^T$로 표현 가능하다.
이때, $\sigma_1 > \sigma_2 > … > \sigma_n$이므로 r번째 이하의 σ를 0으로 취급하여 행렬을 압축하는 것을 Rank-r근사라고 한다.
이때, Rank-r근사에 의한 최소제곱오차는
$\underset{rank{\hat{A}} \leq{r}}{min} \Vert A- \hat{A} \Vert_F = \sqrt{\sigma_{r+1}^2 + \sigma_{r+2}^2 + … + \sigma_{m}^2}$이다.
1. LU-분해
사용분야: 컴퓨터 알고리즘
이유
연립 1차 방정식을 풀 때, 가우스 소거법(행사다리꼴 이용) 이나 가우스-요르단 소거법(기약 행 사다리꼴 이용) 을 사용하였다.
하지만 이 방법은 다음과 같은 특징을 갖는 데이터에서 문제가 있다.
- 컴퓨터 반올림 오차
- 메모리 사용
- 속도
따라서 위와 같은 문제점을 중요하게 여겨야 하는 큰 규모의 문제들을 푸는 데는 적합하지 않다.
2. 거듭제곱법
사용분야: 검색엔진
이유
정방행렬의 고유값을 구하기 위해서는 특성방정식을 풀어야 한다.
하지만 이 과정은 계산상 복잡하고 어렵기 때문에 대부분의 응용에서 직접 이용하기 힘들다.
4) 활용
LU분해
QR분해
그람-슈미트 과정