[Paper Review] Dropout Reduces Underfitting
Source
Contents
0. Abstract
2012년 Hinton이 소개한 dropout은 인공신경망에서 Overfitting을 예방하는 regularizer로써 오랫동안 사용되어 왔다. 본 연구에서는 dropout이 훈련 초기에 사용될 때, underfitting또한 완화할 수 있음을 증명하였다. 우리는 훈련 초기 단계에 dropout은 batch간 gradient의 분산의 방향을 줄이고 batch의 gradient가 전체 데이터셋의 gradient와 정렬되도록 돕든다는 것을 발견했다. 이것은 SGD의 무작위성을 상쇄하고 개별 batch가 훈련에 미치는 영향을 제한하는데 도움을 준다. 우리의 연구 결과로 Underfitting모델의 성능을 향상시키는 방법인 Early Dropout을 제안한다. 이는 Dropout을 훈련 초기에만 적용하고 이후에는 비활성화하는 방식이다. 이를 적용한 모델은 Dropout을 적용하지 않은 모델에 비해 더 낮은 loss를 갖는 것을 확인했다. 또한 우리는 이와 대칭적인 방법인 dropout을 훈련 후반에만 적용하는 late dropout에 대해서도 연구했다. ImageNet 및 다양한 Vision task에 대한 실험에서 우리의 기법이 일반화 정확도를 꾸준히 향상시킨다는 것을 입증했다. 우리의 실험 결과는 딥러닝에서 Regularization에 대한 연구를 활성화 시킬 것이고 우리의 방법은 많은 데이터를 사용하는 미래의 인공신경망 학습에 유용한 도구가 될 것이다.
Dropout의 장점
- SGD의 단점 중 하나인 과도한 Batch의존성을 줄인다.
- Batch의 Gradient를 전체 Dataset의 Gradient와 비슷하게 만든다.
- 초기 훈련에서 gradient의 분산을 줄인다.
- Overfitting방지
- Underfitting방지
1. Introduction
Previous Works
2022년은 딥러닝 시대를 연 AlexNet이후의 10년이 되는 해이다. 이는 AlexNet에서 Overfitting을 방지하기 위해 사용되며 ILSVRC2021의 우승에 중요한 역할을 했던, Dropout도 마찬가지로 10년이 되는 해이다. Dropout이 없었다면 딥러닝의 발전도 수년간 지연되었을 지도 모른다.
Dropout은 딥러닝에서 Overfitting을 방지하기 위한 Regularizer로 사용되었다. 이는 무작위로 neuron을 확률적으로 비활성화하는 방식으로 서로 다른 특징들이 상호 의존하는 것을 막는다. (특정 neuron의 역할이 커지는 것을 막는다는 뜻인듯 함) Dropout을 적용한 이후 train loss는 대부분 증가하지만 test loss는 하락하며 모델의 generalization gap을 줄인다.
Deep learning은 놀라운 속도로 발전해 왔다. 새로운 기술과 architecture들이 꾸준이 소개되었고, 응용 분야가 확장되고 벤치마크도 변화하며 심지어 Convolution도 사라지고 있다. 하지만 dropout은 여전히 사용되고 있다. 이것은 Alphafold와 DALL-E2를 비롯한 최신 AI에서 꾸준히 사용되며 유용함과 효과성을 입증하였다.
Problem(문제 제기)
Dropout의 지속적인 인기에도 불구하고, dropout 비율인 “p”는 꾸준히 감소해왔다. 초기의 dropout의 비율은 0.5로 사용되었지만, BERT나 ViT같은 최근 연구에서는 더 작은 0.1같은 dropout비율이 사용되고 있다.
이러한 trend를 이끄는 주된 요인은 training data가 증가하여 Overfit을 막을 수 있었기 때문이다. 게다가 data augmentation기법과 label이 없거나 wekly-labeled data를 훈련에 사용하는 알고리즘의 발전으로 data를 더 늘릴 수 있었다.그 결과 우리는 overfitting보다는 underfitting문제에 직면하였다.
<dropout의 장점: mini-batch와 full-batch의 alignment>
이 상황에서 dropout의 중요성은 사라질까? 우리의 연구에서는 underfitting을 막기 위한 dropout의 대안적 활용 방법을 제시한다. 우리는 gradient norm에 대한 흥미로운 관찰에서 시작해 droupout의 훈련 역학에 대해 조사했고 실험적 발견에 도달했다. 이것은 초기 훈련에서 dropout은 batch의 gradient의 분산을 줄이고, 모델이 일관된 방향으로 update되도록 유도한다는 것이다. 또한 이 방향은 전체 dataset에 대한 gradient방향과 일치했다. 결과적으로 model은 개별 batch의 영향을 받는 대신, 전체 dataset에 대한 training loss를 더 효과적 최적화할 수 있었다. 한편 dropout은 SGD의 단점을 보완하고, 학습 초기에 무작위적인 sampling때문에 발생하는 과도한 Regularization을 막는다.
Approaches
<dropout의 종류>
이러한 통찰을 기반으로 우리는 학습 초기에만 dropout을 사용해 underfit된 모델을 더 fit하게 도와주는 early dropout을 도입한다. early dropout은 dropout을 사용하지 않거나 표준 dropout을 사용하는 것에 비해 더 낮은 training loss를 갖게 만든다. 반대로 이미 표준 dropout을 사용 했던 모델의 경우 우리는 초기 훈련동안은 dropout을 제거하여 overfitting을 완화하는 방안을 제안한다. 우리는 이 접근 법을 late dropout이라고 부르며 큰 모델에서 generalization성능을 증가시킨다는 것을 입증하였다.
Result
우리는 다양한 모델에서 image classification과 downstream task에서 early dropout과 late dropout을 평가했다. 우리의 방법은 꾸준히 standard dropout이나 dropout을 사용하지 않는 것보다 더 좋은 결과가 있었다. 우리는 우리의 발견이 dropout과 overfitting에 대한 새로운 통찰을 주고 인공 신경망의 regularizer의 발전에 더 좋은 영향을 주기 바란다.
2. Revisiting Overfitting vs. Underfitting
Overfitting
Overfitting은 모델이 train data에 과도하게 지고 unseen data에 대해서는 generalize가 되지 않을 때 발생한다. 모델의 capacity와 dataset의 크기는 training length와 함께 overfitting을 결정 짓는 주요한 요인이다. 큰 모델과 작은 dataset은 overfitting을 일으킬 가능성이 크다. 우리는 이러한 경향을 명확히 하는 간단한 실험들을 진행했다.
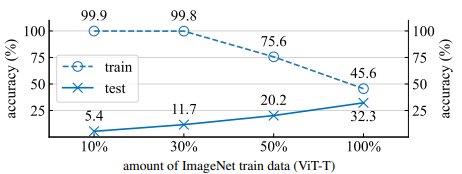
우선 같은 모델에 대해 dataset의 크기를 더 작게 했을 때 train accuracy와 test accuracy의 차이가 증가하는 overfitting을 일으키는 경향을 확인했다. 위 그림은 ViT-Tiny/32로 ImageNet을 학습시킨 결과로 이를 입증하고 있다.
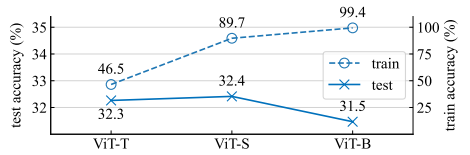
또한 같은 데이터 셋에 대해 모델의 capacity가 증가할 때도 마찬가지로 이러한 차이가 넓어지는 것을 확인할 수 있다. 위 그림은 ViT-T/32, ViT-S/32, ViT-B/32로 ImageNet을 전부 학습시킨 결과이다. 우리는 모든 모델을 data augmentation없이 4000 iteration동안 학습시켰다.
Dropout
우리는 dropout에 대한 간단한 리뷰를 할 예정이다. 각 training iteration동안 dropout layer는 무작위로 각 neuron을 input tensor에 대해 특정 확률로 0으로 만든다. inference동안 모든 neuron들은 활성화 되지만 훈련 단계와 동일한 scale을 유지하기 위해 coefficient로 scaling된다. 각 sample들은 서로 다른 sub-network에 의해 훈련되기 때문에 dropout은 매우 많은 모델에 대한 암묵적 ensemble로써 볼 수 있다. 이것은 딥러닝의 기본적인 구성 요소로 다양한 architecture와 application에서 overfitting을 방지하기 위해 사용되어 왔다.
Stochastic Depth
dropout의 다양한 변형 기법들이 설계되어져 왔다. 이 연구에서는 residual network의 regularizing을 위해 설계된 stochastic depth라고도 불리는 dropout의 변형 또한 고려할 것이다. 각각의 sample과 minibatch에 대해 network는 무작위적으로 residual block의 일부를 생략한다. 이를 통해 model을 더 얕아지게 만들기 때문에 “stochastic depth”라는 이름이 붙게 되었다. 이는 DeiT나 ConvNeXT, MLP-Mixer와 같은 현대의 대부분의 vision network에서 사용되어져왔다. 몇몇 최근 model들은 이를 dropout과 함께 사용한다. stochastic depth는 dropout이 residual block level로 특화된 것으로 볼 수 있고, 우리가 후에 사용하는 dropout은 문맥에 따라 stochastic depth를 포함할 수 있다.
Drop rate
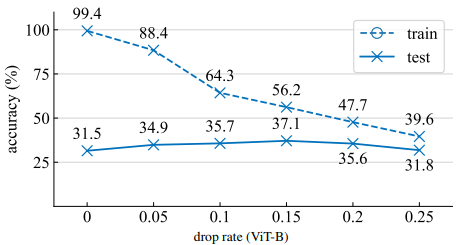
dropout에서 neuron을 0으로 만들 확률은 drop rate p라고 하며 이는 매우 중요한 하이퍼파라미터이다. 예를 들어 Swin Transformers와 ConvNeXt에서는 모델의 크기에 따라 변화하는 유일한 하이퍼 파라미터가 stochastic depth drop rate이다. 우리는 ViT-B를 regularizer하기 위해 dropout을 적용하고 서로 다른 drop rate에 대한 실험을 진행했다. 위 그림에서 볼 수 있듯이 drop rate를 너무 낮게 설정하는 것은 overfitting을 막는데 효과적이지 않고, drop rate를 너무 높게 설정하면 over-regularization되어 test accurary가 낮아진다. 위의 경우, 최적의 drop rate는 0.15였다.
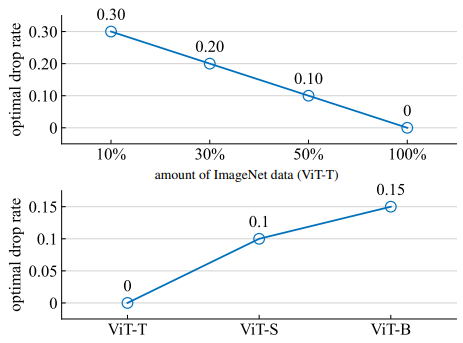
서로 다른 model architecture는 서로 다른 drop rate를 사용하고, 이때 최적의 drop rate p는 model의 size와 dataset의 size에 매우 의존한다. 위 그림은 model과 datasetting별 최적의 drop rate 설정값을 나타낸다. 우리는 0.05간격으로 하이퍼 파라미터 탐색을 수행했다. 위 그림에서 우리는 data가 너무 큰 경우나 model이 너무 작은 경우 최적의 drop rate는 0인 것을 확인했다. 이는 dropout을 사용하는 것이 불필요하고 사용할 경우 model이 underfitting되어 generalization 정확도를 해친다는 것을 의미한다.
Underfitting
문헌에 따르면 dropout에서 사용되는 drop rate는 시간이 지남에 따라 전반적으로 감소해 왔다. VGG나 GoogleNet과 같은 초기 모델들은 0.5나 이보다 더 높은 drop rate를 사용했지만, ViT는 ImageNet에서 이를 0.1로 조정하고 JFT-300M과 같은 큰 dataset으로 pretraining할 때는 dropout을 사용하지 않았다. 또한 최근의 CLIP(language-supervised), MAE(self-supervised)모델에서는 dropout을 사용하지 않았다. 이것은 dataset의 크기증가에 따른 경향이다. model은 대용량 데이터에서는 쉽게 overfit되지 않기 때문이다.
전 세계적으로 생성되고 배포되는 데이터의 양이 급격히 증가하면서 이용 가능한 데이터의 규모는 우리가 훈련하는 모델의 용량을 초과할 가능성이 있다. 하루에 quintillion byte의 데이터가 생성되는 동안 model은 여전히 server나 data center, 모바일 기기와 같은 유한한 물리적 장치에 저장되고 실행되어야 한다. 이러한 상황에서는 미래의 모델들은 데이터에 overfit되기 보다는 적절히 fitting하는 것이 더 어려울 수 있다. 우리의 실험에 따르면 이러한 상황에서 일반적인 dropout은 generalization을 도와주는 regularizer로써 역할을 하지 못한다. 대신에 우리는 model이 대용량의 data에 더 fit하고 underfitting을 줄이는 도구기 필요하다.
3. How Dropout Can Reduce Underfitting
이 연구에서 우리는 dropout이 underfittng을 막을 수 있는 도구처럼 사용될 수 있는지 살펴볼 것이다. 마지막에는 우리가 제안한 도구와 평가방법을 사용해 dropout의 훈련 역학에 대해 자세하 분석을 수행할 것이다. 우리는 두 ViT-T/16(하나는 dropout이 없는 baseline, 다른 하나는 훈련에서 dropout rate가 0.1로 설정된 모델)의 ImageNet에서의 훈련 과정을 비교할 것이다.
Gradient Norm & Model distance
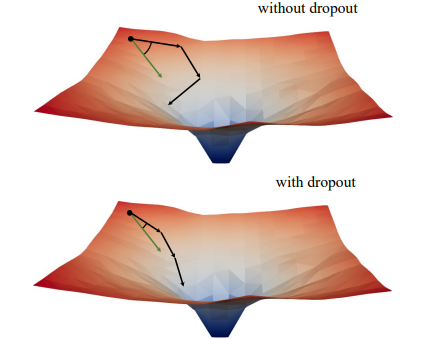
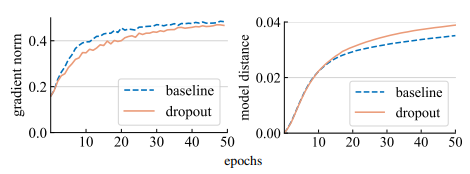
우리는 $L_2 \text{norm} \Vert g \Vert_2$를 측정하여 dropout이 gradient g의 강도에 미치는 영향을 분석하기 시작했다. 우리는 dropout model에서는 비록 일부의 가중치가 비활성화 되었을지라도 전체 모델의 gradient를 측정하였다. 그림(왼쪽)에서 볼 수 있듯이 dropout model은 더 작은 norm의 gradient를 생성하고, 이는 각 gradient의 update마다 더 작은 step을 갖도록 한다는 것을 말한다.
Gradient step이 더 작다면 우리는 dropout model이 baseline model보다 초기 지점에서 더 작은 거리를 움직인 다는 것을 알 수 있다. 이를 측정하기 위해 우리는 $L_2 norm, (\Vert W_1 - W_2 \Vert_2)$으로 두 모델간의 이동 거리를 측정하였다. 그림(오른쪽)에 보면 우리는 random하게 초기화 되었던 각 모델의 이동 거리를 표시하였다. 그러나 Gradient norm을 바탕으로 한 초기 예상과 달리 dropout model이 baseline model보다 더 큰 거리를 이동했다는 점이 놀라웠다.
두 사람이 걷는 상황을 상상해 보자. 한 사람은큰 걸음을 걷고 다른 사람은 작은 걸음을 걷는다. 그럼에도 불구하고 작은 걸음을 걷는 사람이 같은시간 동안 시작점에서 더 먼 거리를 이동할 수 있다. 왜 그런가? 이는 작은 걸음을 걷는 사람이 더 일관된 방향으로 걷는 반면에 큰 걸음을 걷는 사람은 무작위로 방향을 바꾸며 진전이 없기 때문일 수 있다.
Gradient direction variance
우리는 두 모델에 대해 dropout model이 mini batch간 더 일관된 gradient방향을 생성한다는 가설을 새웠다. 이를 평가하기 위해서 우리는 random하게 선택된 batch에서 모델의 checkpoint를 학습시키며 gradient G의 집합을 수집했다. 우리는 평균 Cosine거리를 계산하여 gradient의 방향에 대한 분산을 측정하는 방법인 GDV를 제안한다.
\[GDV = \frac{2}{\vert G \vert \cdot (\vert G \vert - 1)}\sum_{g_i, g_j \in G \\ i \neq j} \frac{1}{2} (1 - \frac{<g_i, g_j>}{\Vert g_i \Vert_2 \cdot \Vert g_j \Vert_2})\]
- $\frac{2}{\vert G \vert \cdot (\vert G \vert - 1)}$
- $\rightarrow$ 1 / (G에서 사용 가능한 gradient 쌍의 개수)
- $\sum_{g_i, g_j \in G \ i \neq j} \frac{1}{2} (1 - \frac{<g_i, g_j>}{\Vert g_i \Vert_2 \cdot \Vert g_j \Vert_2})$
- $\rightarrow$ 두 gradient가 가까우면 0, 멀면 1이 되도록 변형한 식
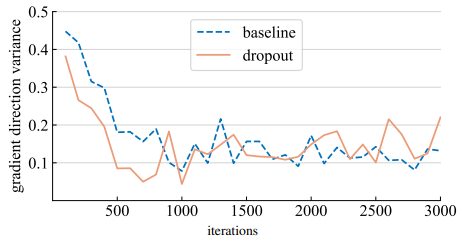
위 그림은 우리의 가설에 힘을 실어주는 분산 비교 결과이다. 거의 1000 iteration까지 dropout 모델은 더 작은 gradient분산을 나타내고 더 일관된 방향으로 움직인다. 주목할 만하게도 앞선 연구들은 gradient의 분산을 측정하거나 gradient의 분산을 줄이기 위한 방법을 제안했다. 하지만 우리의 측정 지표는 오직 gradient의 방향만을 고려하고 각각의 gradient가 전체 측정에서 동등하게 기여한다는 점에서 이와 다르다.
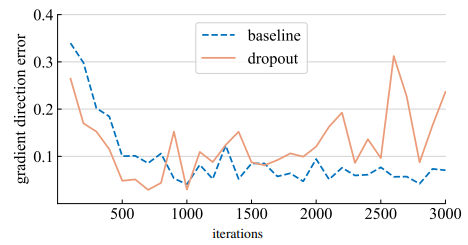
Gradient direction error
\[GDE = \frac{1}{\vert G \vert} \sum_{g_{step} \in G} \frac{1}{2}(1-\frac{<g_{step}, \hat{g}>}{\Vert g_{step} \Vert_2 \cdot \Vert \hat{g} \Vert_2})\]그러나 아직 “올바른 Gradient의 방향은 무엇인가?”라는 질문은 해결되지 않았다. training data에 fit하기 위해서는 objective function이 mini-batch가 아니라 full-batch에 대해 loss를 minimize해야 한다. 우리는 주어진 모델에 dropout을 inference모드로 변경한 후 전체 training set에 대한 gradient를 계산했다. 이제 우리는 실제 mini-batch gradient $g_{step}$이 전체 dataset에 대한 “ground truth” gradient인 $\hat{g}$와 얼마나 먼지 평가해야 한다. 우리는 $g_{step}$의 $\hat{g}$와의 평균 cosine거리를 grident 방향 오류(GDE)로 정의한다.
우리는 이 GDE를 계산한 후에 위의 그림에 표시하였다. 훈련 초기에 dropout model의 mini-batch gradient는 full-batch gradient보다 더 작은 편차를 갖고 있었다. 이는 총 training loss를 최적화 하는데 더 적합한 방향으로 이동하고 있음을 나타낸다. 그러나 거의 1000 iteration이후 dropout model은 전체 gradient로 부터 더 멀어진 gradient를 생성한다. 이는 dropout이 underfitting을 줄이는 것에서 overfitting을 줄이는 것으로 전환되는 전환점일 수 있다.
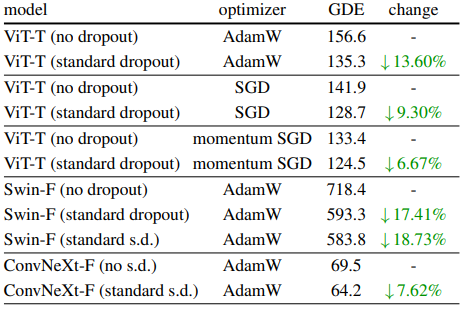
위의 실험은 ViT와 AdamW를 사용해 최적화한 결과이다. 우리는 이러한 관찰 결과가 다른 optimizer와 architecture에서 일관되게 나타나는지 살펴보았다. GDE감소에 대한 영향을 정량화하기 위해 우리는 GDE와 Iteration 그래프에서 처음 1500번의 반복동안 곡선 아래 면적(AUC)을 측정했다. 이는 이 기간동안 평균 GDE를 나타내며 AUC값이 클수록 초기에 GDE가 더 컸음을 의미한다. 위 표는 그 결과이고 GDE의 감소는 다른 Optimizer(SGD)와 architecture(Swin)사이에서도 발생한 것을 확인할 수 있다.
Bias and Variance for gradient estimation
초기 학습에서의 이러한 분석은 bias-variance tradeoff의 관점에서도 해석할 수 있다. dropout이 없는 모델들은 SGD mini-batch는 전체 데이터셋 gradient에 대한 편향이 없는 추정치를 제공한다. 이는 mini-batch의 gradient가 전체 dataset의 gradient와 일치하고 각 mini-batch가 동일한 network를 통과하기 때문이다. 그러나 dropout을 사용하면 mini-batch gradient는 서로 다른 sub-network에 의해 생성되기 때문에 이 추정치는 편향을 갖게된다. 따라서 full-batch gradient와는 다른 값을 갖게 되는데, 그럼에도 불구하고 우리의 실험에서는 이 gradient varience가 상당히 줄어들었다. 직관적으로 이 variance와 error의 감소는 model이 많은 변화를 겪는 훈련 초기에, 특정 batch에 overfitting되는 것을 막아준다고 생각할 수 있다.
4. Approach
위에서 분석한 것을 바탕으로 우리는 dropout을 일찍 사용하는 것은 model이 training data에 fit 능력을 잠재적으로 향상시켜준 다는 것을 알 수 있다. 이를 바탕으로 다음과 같은 접근법을 제안한다.
Underfitting and overfitting regime
훈련 데이터를 더 fit 하는 것이 바람직한지는 모델이 underfitting된 상태인지 overfitting된 상태인지에 따라 달라지고, 이를 정확히 정의하는 것은 어렵다. 이 연구에서 우리는 다음과 같은 기준을 사용하고 이것이 우리의 목표에 효과적임을 발견했다.
- Overfitting
- 표준 dropout을 사용했을 때 성능이 더 나아질 경우
- Overfitting
- Underfitting
- 표준 dropout을 사용하지 않고도 성능이 더 나아질 경우
- Underfitting
모델의 상태는 모델 아키텍처뿐만 아니라 사용된 데이터셋과 기타 훈련 매개변수에도 의존한다.
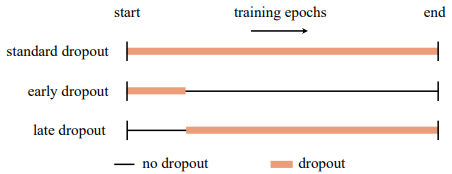
Early dropout
기본 설정에서 underfitting상태에 있는 모델은 dropout을 사용하지 않는다. 훈련 데이터를 더 fit하게 하는 능력을 향상시키기 위해 early dropout을 제안한다. 이는 특정 iteration까지 dropout을 사용하고 이후에는 비활성화 하는 방식이다. 우리의 실험은 earl dropout이 최종 훈련 손실을 줄이고 정확도를 향상시킨다는 것을 보여준다.
Late dropout
overfitting된 모델은 이미 표준 dropout을 훈련 설정에 포함하고 있다. 훈련 초기 단계에서는 dropout이 의도치 않게 overfitting을 유발할 수 있고 이는 바람직하지 않다. overfitting을 줄이기 위해 우리는 late dropout을 제안한다.이는 특정 iteration까지 dropout을 사용하지 않고 이후 훈련에서 사용한다. 이는 early dropout과 대칭적인 방법이다.
Hyper-parameters
우리의 방법은 개념적인 면과 구현적인 면에서 모두 간단하다. 이는 2가지 하이퍼 파라미터가 필요하다.
- dropout을 활성화하거나 비활성화하기 전에 기다리는 epoch 수
$\rightarrow$ 1%와 50% 사이에서 robust하게 동작한다. - drop rate p
내 결론
훈련 초기에는 underfitting을 막는 용도 → gradient의 방향을 일치 시키는 효과(일관된 방향, 안정적 학습) 때문에 → gradient방향일치 효과 > regularization
훈련 후기에는 overfitting을 막는 용도 → gradient의 방향을 일치시키는 효과보다 서로다른 sub-network를 사용해 암묵적 ensemble의 효과가 더 커짐 → gradeint방향일치 효과 < regularization
역할1: gradient의 방향 일치 역할2: 암묵적 ensemble(regularization)