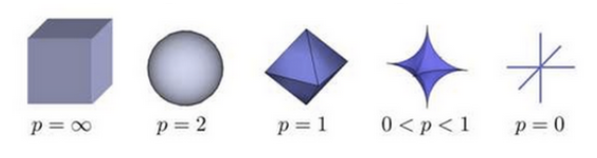포스트

1. Convex Set

게시 업데이트
By UI-JIN KIM 12 분읽는 시간

Convex Optimization

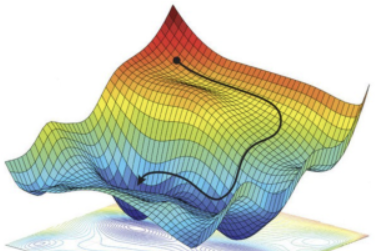
1. Optimization

1) 정의

alt text

Object Function을 주어진 Constraints하에, Minimize하는 것.
(이를 “Programming, 계획법”이라고도 함. (Coding을 의미하는 것이 아님))

  • 주로 이때, Minimize하는 정의역의 값(변수 값)을 찾는 것이 목표

Maximize

“$f(x)$”를 Maximize하는 문제는 “$-f(x)$”를 Minimize하는 문제로 변환이 가능하다.
즉, Maximize문제와 Minimize문제는 근본적으로 같은 문제이다.

Example

$f_0(x) = x^2-2x+4$, $(0 \leq x \leq 5)$ 일 때,
$f_0(x)$를 최소화 하는 x 찾기

2) 특징

모든 문제는 최적화 문제로 변환이 가능하다.

하지만 아래의 예시들을 보면 알 수 있듯이 Constraints의 존재 때문에 Optimization을 하는 것은 대부분 매우 어렵다.

ex1. Machine Learning

  • Object Function
    Minimize Loss Function
  • Constraints
    가중치의 수, Layer의 수, Input Dimension, Output Class의 수, …

ex2. Resource Planning

  • Object Function
    Minimize Total Cost
  • Constraints
    재료의 비용, 운송 비용, 시간적 한계, …

ex3. Physics

  • Object Function
    Maximize Entropy
  • Constraints
    초기 온도, 에너지 보존법칙, …

3) Convex Optimization

alt text

What?

Convex Optimization은 무엇일까?
Optimization 상황에서 다음과 같은 상황에 해당하는 경우를 의미한다.

  • Optimization Function $\rightarrow$ Convex Function
  • Constraints $\rightarrow$ Convex Set

Why?

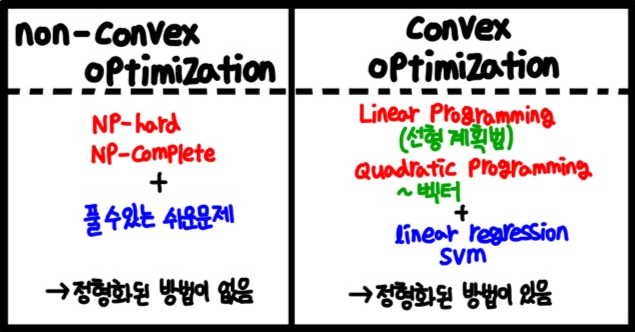
그렇다면 Convex Optimization을 공부하는 이유는 무엇일까?

대부분의 최적화 문제들은 풀기 어렵다고 알려져 있지만,
이 중 Convex Optimization 문제들은 정형화된 방법(Known Algorithm)으로 푸는 것이 가능하다.

즉, 만약 Convex Optimization 문제가 아니라고 하더라도 다음과 같이 풀 수 있다.

  • Convex Optimization문제가 되도록 변형한다.
  • 최적의 해는 아니더라도 좋은 해(차선의 해)를 찾는다.

다시말해, 이 문제가 풀 수 있는 문제인지를 알기 위해
이 문제가 Convex Optimization문제인지 먼저 판단하는 것이 중요하다.

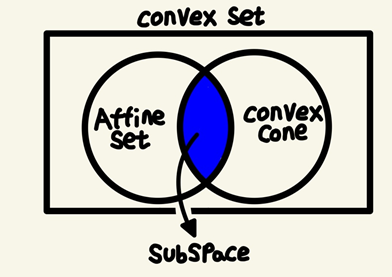
2. Some Sets

alt text

Convex Set은 Convex Function의 정의역 역할을 한다.
이 챕터에서는 Convex Set의 정의를 알아보기 위해 몇가지 집합들의 공간에 대해 살펴보자.

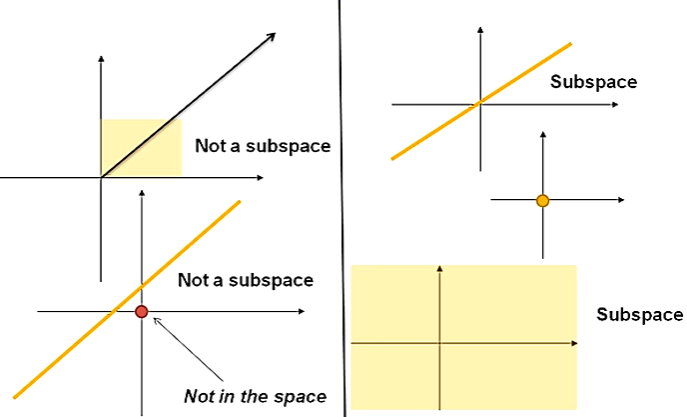
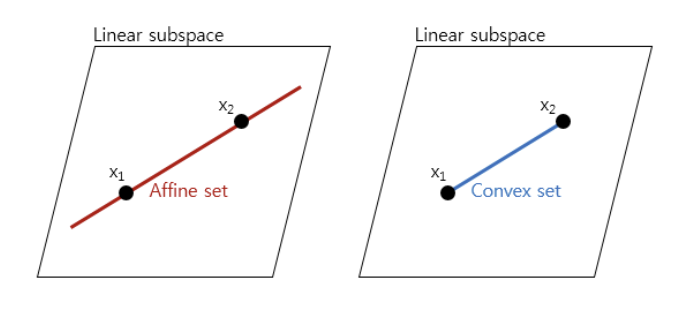
1) Subspace

alt text

ⅰ. Plane

$\begin{Bmatrix}\theta_1 \textbf{x}_1 + \theta_2 \textbf{x}_2 | \theta \in \mathbb{R} \end{Bmatrix}$

위와 같이 여러 벡터들의 Linear Combination의 형태를 갖는다.

  • 이 공간을 최소한의 수의 벡터로 표현할 때, 이 벡터들을 기저벡터라고 한다.

ⅱ. Subspace

조건-

Linear Combination 이란?

  • $\begin{Bmatrix}\textbf{x} = \theta_1 x_1 + \theta_2 x_2 + … + \theta_n x_n | \theta \in \mathbb{R} \end{Bmatrix}$

2) Affine Sets

alt text

ⅰ. Lines

$\begin{Bmatrix}\theta \textbf{x}_1 + (1-\theta)\textbf{x}_2 | \theta \in \mathbb{R} \end{Bmatrix}$

위와 같이 가중치의 합이 1이되는 점들의 Linear Combination은 하나의 Line의 형태를 갖는다.

  1. 증명
    • $\textbf{x}_2 + \theta(\textbf{x}_1 - \textbf{x}_2)$로 변환 가능
      → $\textbf{x}_2$ 를 지나고 $ (\textbf{x}_1 - \textbf{x}_2)$ 와 평행한 점들의 모임

ⅱ. Affine Sets

$\begin{Bmatrix}\theta \textbf{x}_1 + (1-\theta)\textbf{x}_2 \in \mathcal{A} | (x_1, x_2) \in \mathcal{A}, \theta \in \mathbb{R} \end{Bmatrix}$

즉, $\mathcal{A}$ 의 원소 2개를 이어 만든 직선이 전부 $\mathcal{A}$ 에 속해야 한다.

  1. 예시
    • $\textbf{x}$ 의 범위가 주어지지 않은 평면
    • $\textbf{x}$ 의 범위가 주어지지 않은 직선
    • $S = \begin{Bmatrix} \textbf{x} | A\textbf{x}=\textbf{b} \end{Bmatrix}$
  2. 예시 3 증명
    • $\textbf{x}_1, \textbf{x}_2 \in S$ 라고 할 때, $\theta \textbf{x}_1 + (1-\theta) \textbf{x}_2$ 에 대하여
      $A \begin{Bmatrix} \theta \textbf{x}_1 + (1-\theta) \textbf{x}_2 \end{Bmatrix} = \theta A \textbf{x}_1 + A\textbf{x}_2 -\theta A \textbf{x}_2 = \theta \textbf{b} + \textbf{b} - \theta \textbf{b} = \textbf{b}$ 이기 때문에,
      $\theta \textbf{x}_1 + (1-\theta) \textbf{x}_2$(직선 위의 모든 점) 또한 $\mathcal{A}$ 에 속한다.

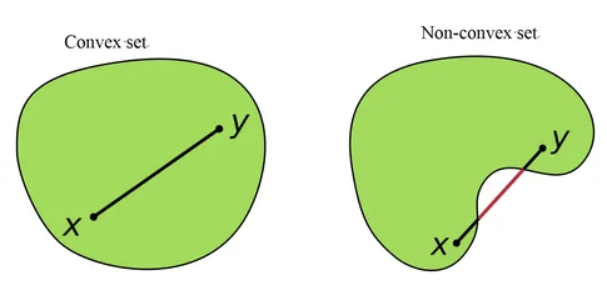
3) Convex Set

alt text

ⅰ. Line Segment

$\begin{Bmatrix}\theta \textbf{x}_1 + (1-\theta)\textbf{x}_2 | \theta \in \mathbb{R}, 0 \leq \theta \leq 1 \end{Bmatrix}$

Lines의 정의에서 $\theta$ 의 범위를 위와 같이 0과 1 사이로 한정하면 선분이 된다.

ⅱ. Convex Set

$\begin{Bmatrix}\theta \textbf{x}_1 + (1-\theta)\textbf{x}_2 \in \mathcal{A} | (x_1, x_2) \in \mathcal{A}, \theta \in \mathbb{R}, 0 \leq \theta \leq 1 \end{Bmatrix}$

  1. 예시
    • 다면체(다각형)
    • 원, 타원

Convex Combination 이란?

  • $\begin{Bmatrix}\textbf{x} = \theta_1 x_1 + \theta_2 x_2 + … + \theta_n x_n | \theta \in \mathbb{R}, \theta \geq 0, \sum \theta_i = 1\end{Bmatrix}$

이때, Convex Combination은 확률과 비슷한 성질을 갖는다는 점을 기억해 두자.

3. Convex Set

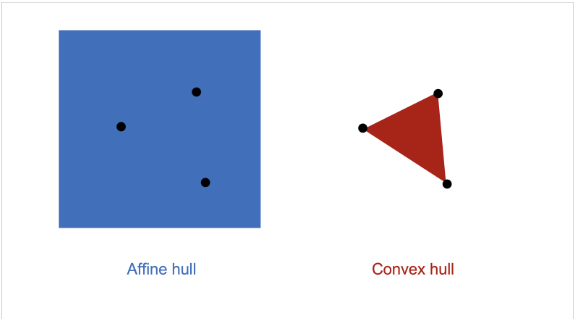
1) Convex Hull

alt text

$Conv(S) = \begin{Bmatrix}\theta_1 x_1 + \theta_2 x_2 + … + \theta_n x_n | x_i \in \mathcal{S}, \theta_i \geq 0 , \sum \theta_i = 1\end{Bmatrix}$

  • 정의
    • 어떤 점들로 표현할 수 있는 모든 Convex Combination을 원소로 갖는 집합
    • 즉, 집합 S를 포함하는 가장 작은 Convex Set

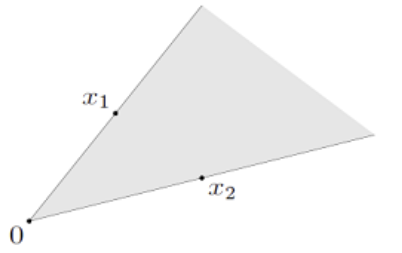
2) Convex Cone

alt text

$\begin{Bmatrix}\theta_1 x_1 + \theta_2 x_2 + … + \theta_n x_n | x_i \in \mathcal{S}, \theta_i \geq 0 \end{Bmatrix}$

  • 정의
    • 어떤 점들로 표현할 수 있는 모든 Conic Combination을 원소로 갖는 집합
  • 주의: Convex Cone은 반드시 원점을 포함한다.
    • 특정 $\theta_i=0$ 인경우: 가장자리
    • 모든 $\theta_i=0$ 인경우: 원점

Conic Combination 이란?

  • $\begin{Bmatrix} \textbf{x} = \theta_1 x_1 + \theta_2 x_2 + … + \theta_n x_n \in \mathcal{S} | x_i \in \mathcal{S}, \theta_i \geq 0 \end{Bmatrix}$

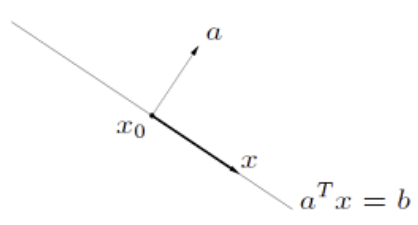
3) Hyperplanes

alt text

$\begin{Bmatrix} x |a^T \textbf{x} = b \end{Bmatrix}, a \neq 0, b=a^T \textbf{x}_0$

  • 정의
    • 벡터 $a$ 에 수직인 면
  • 주의: 두 벡터 $a, b$ 의 내적은 $a^Tb$로 표현할 수 있다.
    • 일반적인 벡터는 $n \times 1$ 의 열벡터를 나타내기 때문
    • 평면의 방정식: $a^T(\textbf{x}-x_0) = (a, b, c) \cdot (x_1 - x_0, x_2 - x_0, x_3 - x_0)$
  • Affine Set
  • Convex Set

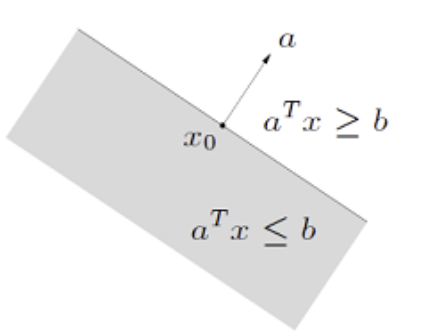
4) Halfspaces

alt text

$\begin{Bmatrix} x |a^T \textbf{x} \leq b \end{Bmatrix}, a \neq 0, b=a^T \textbf{x}_0$

  • 정의
    • Hyperplane을 경계면으로 하는 공간
  • 특징
    • $a^T(\textbf{x}-x_0) \leq 0$
      $\rightarrow$ 내적이 음수 $\rightarrow$ 벡터 $a$와 둔각을 이루는 공간
    • $a^T(\textbf{x}-x_0) \geq 0$
      $\rightarrow$ 내적이 양수 $\rightarrow$ 벡터 $a$와 예각을 이루는 공간
  • Convex Set

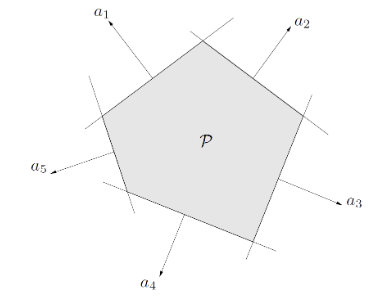
5) Polyhedra

alt text

$\begin{Bmatrix} x | \textbf{A} \textbf{x} \leq \textbf{b} , \textbf{C} \textbf{x} = d\end{Bmatrix}$

  • 정의
    • 유한한 개수의 Hyperplane과 Halfspace의 교집합
  • 의미
    • $\textbf{A} \textbf{x} \leq \textbf{b}$ 는 다음과 같이 다시 쓸 수 있다. \(\begin{bmatrix}-\textbf{a}_1^T-\\ -\textbf{a}_2^T- \\ ... \\ -\textbf{a}_n^T- \end{bmatrix} \begin{bmatrix}\textbf{x}_1\\ \textbf{x}_2\\ ...\\ \textbf{x}_n \end{bmatrix} \leq \begin{bmatrix}b_1\\ b_2\\ ...\\ b_n \end{bmatrix}\)
    • $\textbf{C} \textbf{x} = \textbf{d}$ 는 다음과 같이 다시 쓸 수 있다. \(\begin{bmatrix}-\textbf{c}_1^T-\\ -\textbf{c}_2^T- \\ ... \\ -\textbf{c}_n^T- \end{bmatrix} \begin{bmatrix}\textbf{x}_1\\ \textbf{x}_2\\ ...\\ \textbf{x}_n \end{bmatrix} = \begin{bmatrix}d_1\\ d_2\\ ...\\ d_n \end{bmatrix}\)
    • 즉, 여러 Halfspace들과 Hyperplane들을 나타내는 식이 된다.
  • Convex Set

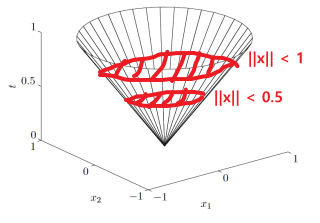
6) NormCone & NormBall

alt text

NormCone: $\begin{Bmatrix}(\textbf{x}, t)| \Vert \textbf{x} \Vert \leq t \end{Bmatrix}$
($\textbf{x}$는 Vector, $t$는 Scalar, NormCone: n+1차원 Vector)

Norm의 성질

  • $\Vert x \Vert_p = (\sum\limits_{i} |x_i|^p)^{\frac{1}{p}}$
  • $\Vert x \Vert \geq 0$
  • $\Vert tx \Vert = |t| \Vert x \Vert$ for $t \in \mathbb{R}$
  • $\Vert x + y \Vert \leq \Vert x \Vert + \Vert y \Vert$ (삼각부등식)

참고: (2, 3, 5)의 $\infty$ Norm

$\Vert \textbf{x} \Vert_\infty = \lim\limits_{p\rightarrow \infty}(2^p +3^p +5^p)^\frac{1}{p} \approx \lim\limits_{p\rightarrow \infty}(5^p)^\frac{1}{p} = 5$
즉, $max(\textbf{x})$ 를 나타낸다.

alt text

NormBall: $B_p(x_0, r) = \begin{Bmatrix}x | \Vert x-x_0 \Vert_p \leq r\end{Bmatrix}$
(p=2인 경우 Euclidean ball)

  • $B_1(O, r) \subset B_2(O, r) \subset B_\infty(O, r)$

Convex Set 증명

$(x_1, x_2) \in B$ 에 대하여 $(\theta x_1 + (1-\theta) x_2 \in B)$ 가 성립하는지 확인해 보자
\(\Vert \theta x_1 + (1-\theta) x_2 - x_0 \Vert_p \\ = \Vert \theta x_1 + (1-\theta) x_2 - \theta x_0 - (1-\theta)x_0 \Vert_p \\ = \Vert \theta (x_1-x_0) + (1-\theta)(x_2 - x_0) \Vert_p \\ \leq \Vert (\theta(x_1 - x_0) \Vert + \Vert(1-\theta)(x_2 - x_0)\Vert_p \\ \leq \theta r + (1-\theta) r \\ = r \\ \therefore \Vert \theta x_1 + (1-\theta) x_2 - x_0 \Vert_p \leq r\)

4. Theory

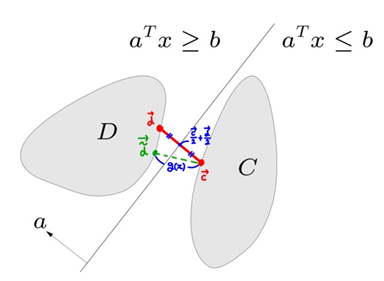
1) Seperating Hyperplane Theorem

alt text

2개의 만나지 않는 Convex Set $C, D$가 있을 때
이 두 Convex Set을 나누는 Hyperplane $\begin{Bmatrix}x | \textbf{a}^T \textbf{x} = b \end{Bmatrix}$이 반드시 하나이상 존재한다.

증명

두 Convex Set이 가장 가까워지는 순간 $C, D$ 위의 점을 $\vec{c}, \vec{d}$라고 하자.
또한, Hyperplane은 이 두 점을 잇는 직선을 수직이등분하여 지나간다.

ⅰ. Hyperplane의 방정식: $a^T\textbf{x} = b$

  • Hyperplane의 $a^T = \vec{d} - \vec{c}$
  • Hyperplane의 $b = \frac{\Vert d \Vert^2 - \Vert c \Vert^2}{2}$
    $\rightarrow \because b = \textbf{a}^Tx_0 = (\vec{d} - \vec{c})(\frac{\vec{d} + \vec{c}}{2})$

ⅱ. Convex Set $D$위의 임의의 점 $\hat{d}$가 $d$보다 더 가깝다고 가정

  • $\vec{d}-\vec{c} \geq \vec{\hat{d}} - \vec{c}$

ⅲ. Taylor전개: $\bigtriangleup g = (2d - 2c)^T(\hat{d}-d)$

  • $\bigtriangleup f(\textbf{x}) \approx \nabla f(x_0)^T (x-x_0)$
    $\rightarrow$어떤 점 $x_0$ 에서 다른 점 $\textbf{x}$ 까지 이동할 때 함수의 변화를 근사하는 식
  • 임의의 점에서 C까지의 거리 방정식 = $g(\textbf{x}) = \Vert \textbf{x} - \textbf{c} \Vert^2 = (\textbf{x} - c)^T(\textbf{x} - c)$
    $= x^Tx - x^Tc - c^Tx + c^Tc$
  • $\nabla \textbf{x}^T\textbf{x} = 2\textbf{x}$, (전개 후 유도 가능)
  • $\textbf{x}^T\textbf{c} = \textbf{c}^T\textbf{x}$

ⅳ. Taylor전개가 음수임을 증명

  • Talyor전개가 음수임을 알면 $\vec{d}-\vec{c} \geq \vec{\hat{d}} - \vec{c}$ 가 거짓임을 알 수 있다. \(\bigtriangleup g = (2d - 2c)^T(\hat{d}-d) = 2(- \Vert d \Vert^2 + (d-c)^T\hat{d} + c^Td) \\ \leq 2(-\Vert d \Vert^2 + \frac{\Vert d \Vert^2 - \Vert c \Vert^2}{2} + c^Td) \\ = -\Vert d \Vert^2 - \Vert c \Vert^2 + 2c^T d = -\Vert d-c \Vert^2 < 0\)

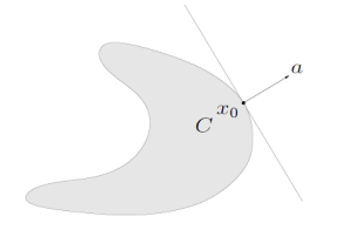
2) Supporting Hyperplane Theorem

alt text

Convex Set의 접평면 $a^Tx_0$에 대해 Convex Set의 모든 원소는 이 접평면 아래에 존재한다.
즉, 모든 $x \in C$에 대해 $a^Tx \leq a^Tx_0$를 만족할 때
$\begin{Bmatrix} x | a^Tx = a^Tx_0 \end{Bmatrix}$ 인 Hyperplane은 집합 C의 Supporting Vector이다.

3) Convexity Preserving

alt text

$C, C_1, C_2$ 가 Convex Set일때, 다음도 Convex Set이다.

  • Intersection
    $C_1 \cap C_2$
  • Scaling
    $aC = \begin{Bmatrix} a\textbf{x} | \textbf{x} \in C\end{Bmatrix}$
  • Translation
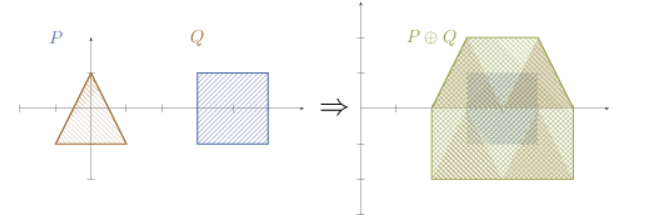
    $a+C = \begin{Bmatrix} a + \textbf{x} | \textbf{x} \in C\end{Bmatrix}$
  • Minkowski Addition
    $A\oplus B = \begin{Bmatrix} \textbf{x} + \textbf{y} | \textbf{x} \in A, \textbf{y} \in B \end{Bmatrix}$

(Union(합집합)은 Convexity Preserving이 되지 않는다.)

Math, Convex Optimization
math
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.