2. Convex Function
Convex Function
이번에는 주어진 문제가 Convex Function인지 알아보는 방법에 대해 공부해 보자.
1. Definition
1) 정의
Convex
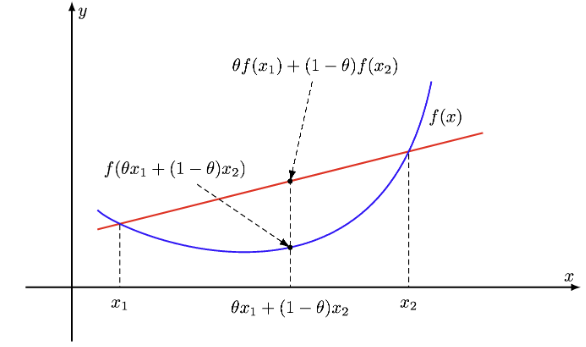
$f$의 Domain $\mathcal{D}(f)$가 Convex Set이고 $0 \leq \theta \leq 1$일 때, 모든 $\mathbf{x}_1 \mathbf{x}_2 \in \mathcal{D}(f)$에 대해
$f(\theta \mathbf{x}_1 + (1-\theta) \mathbf{x}_2) \leq \theta f(\mathbf{x}_1) + (1-\theta)f(\mathbf{x}_2)$가 성립하는 함수
- Concave: $-f$
Strictly Convex
$f$의 Domain $\mathcal{D}(f)$가 Convex Set이고 $0 < \theta < 1$일 때, 모든 $\mathbf{x}_1 \mathbf{x}_2 \in \mathcal{D}(f)$에 대해
$f(\theta \mathbf{x}_1 + (1-\theta) \mathbf{x}_2) < \theta f(\mathbf{x}_1) + (1-\theta)f(\mathbf{x}_2)$가 성립하는 함수Restriction to line
복잡한 함수의 Convexity를 확인하는 방법중 하나는 함수의 단면을 살펴보는 것이다.
$f(x)$가 Convex이다. $\Leftrightarrow$ $a+bt \in \mathcal{D}(f)$일때 $g(t)=f(a+bt)$가 Convex이다.
(Proof)
ⅰ. if $g(t)$ is Convex
$\Rightarrow \theta g(t_1) + (1-\theta) g(t_2) \geq g(\theta t_1 + (1-\theta) t_2)$
$\Rightarrow \theta f(a+bt_1) + (1-\theta) f(a+bt_2) \geq f(\theta (a+bt_1) + (1-\theta)(a+bt_2))$
$a+bt_i = \mathbf{x}_i$
$\Rightarrow \theta f(\mathbf{x}_1) + (1-\theta)f(\mathbf{x}_2) \geq f(\theta \mathbf{x}_1 + (1-\theta) \mathbf{x}_2)$
$\therefore f(x)$ 또한 Convex이다.(Example)
Log Determinant $f(A) = \text{log}(det(A)), \qquad g(t) = f(A+tB)$, $\qquad C=A^{-\frac{1}{2}}BA^{-\frac{1}{2}}$
$g(t) = \text{log}(det(A+tB)) = \text{log}(det(A^{\frac{1}{2}}(I+tA^{-\frac{1}{2}}BA^{-\frac{1}{2}})A^{\frac{1}{2}}))$
$\;\;\;\quad = \text{log}(det(A^{\frac{1}{2}})) + \text{log}(det(A^\frac{1}{2})) + \text{log}(det(I+tC))$
$\;\;\;\quad = 상수 + \text{log}(det(I+tC)) = 상수+\text{log}(det(I + tU\Lambda U^T))$
$\quad\;\;\; = 상수 + \text{log}(det(UU^T + tU\Lambda U^T))= 상수 + \text{log}(det(U(I + t\Lambda)U^T))$
$\;\;\;\quad = 상수 + \text{log}(det(UU^T(I+t\Lambda)) = 상수 + \text{log}(det(I+t\Lambda))$
$\;\;\;\quad = 상수+ \text{log}(\prod \limits_i^n (1+ t \lambda_i)) = 상수 + \sum \limits_i^n log(1+t\lambda_i)$
즉, $f(A)$는 Concave함수에 Affine함수가 합성된 Concave함수이다.
$※ det(AB) = det(A)det(B)$
$\quad$ Symmetric일 경우 $UU^T=U^TU = I$
2) Example
$\mathbb{R} \rightarrow \mathbb{R}$
Function 수식 Convex Function Concave Function Affine $ax + b$ O O Exponential $e^{ax}$ O X Powers $x^{\alpha}$ $\alpha \leq 0 \quad \alpha \geq 1$ $0 \leq \alpha \leq 1$ Powers of absolute value $|x|^p$ $p \geq 1$ Negative Entropy $x log x$ $x>0$ X Logarithm $log x$ X $x > 0$ $\mathbb{R}^n \rightarrow \mathbb{R}$
Function 수식 Convex Function Concave Function Affine
(Hyper Plane)$a^T\mathbf{x} + b$ O O p-norms $\Vert \mathbf{x} \Vert_p := (\sum \limits_i \vert \mathbf{x}_i \vert ^p)^{\frac{1}{p}}$ O X 삼각부등식(p-norms 증명)
$ f(\mathbf{x}) = \Vert \mathbf{x} \Vert_p$
$ f(\theta \mathbf{x}_1 + (1- \theta) \mathbf{x}_2) = \Vert \theta \mathbf{x}_1 + (1- \theta) \mathbf{x}_2 \Vert \leq \theta \Vert \mathbf{x}_1 \Vert + (1-\theta) \Vert \mathbf{x}_2 \Vert = \theta f(\mathbf{x}_1) + (1-\theta)f(\mathbf{x}_2)$$\mathbb{R}^{m \times n} \rightarrow \mathbb{R}$
Function 수식 Convex Function Concave Function Affine $f(X) = \sum \limits_{i=1}^m \sum \limits_{j=1}^n A_{ij} X_{ij} + b$
$\qquad\;\, = tr(A^TX) + b$O O Matrix Norm $\Vert A \Vert_2 = \max \limits_x \frac{\Vert AX \Vert_2}{\Vert X \Vert_2} = \sigma_{max}(A)$
$\qquad \;\, = \sqrt{\max \limits_x \frac{X^TA^TA X}{X^T X}}$
$\qquad\qquad$(Rayleigh Quotient)O X 삼각부등식
$\Vert A + B \Vert = \max \limits_\mathbf{x} \frac{\Vert (A+B)\mathbf{x} \Vert}{\Vert \mathbf{x} \Vert} \leq \max \limits_\mathbf{x} \frac{\Vert A \mathbf{x} \Vert + \Vert B \mathbf{x} \Vert}{\Vert \mathbf{x} \Vert} \leq \max \limits_\mathbf{x} \frac{\Vert A \mathbf{x} \Vert}{\Vert \mathbf{x} \Vert} + \max \limits_\mathbf{x} \frac{\Vert B \mathbf{x} \Vert}{\Vert \mathbf{x} \Vert} = \Vert A \Vert + \Vert B \Vert$
3) 활용
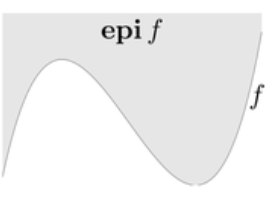
Epigraph & Sublevel Set
Jensen’s Inequality
이 Convex Function의 정의는 젠슨부등식에서도 엿볼 수 있다.
\[f(\mathbb{E}[z]) \leq \mathbb{E}[f(z)]\]
- Convex의 정의로부터 쉽게 유추가능하다
$f(\theta \mathbf{x}_1 + (1-\theta) \mathbf{x}_2) \leq \theta f(\mathbf{x_1}) + (1-\theta)f(\mathbf{x}_2)$
$\rightarrow 0 \leq \theta \leq 1$
$\rightarrow$ 확률로 생각
2. Condition
1) 정의
PSD 판별 방법
1. 정의(고윳값) 2. $\mathbf{v} \mathbf{v}^T$ 또는 $\mathbf{v}^T \mathbf{v}$ 꼴로 변형 3. 실베스터 판정법 $f(x) = \mathbf{x}^TA\mathbf{x}$
$= \mathbf{y}^T \Lambda \mathbf{y} = \sum \limits_i \lambda_i y_i^2$만약 $\mathbf{v} \mathbf{v}^T$이면 $\mathbf{x}^T \mathbf{v} \mathbf{v}^T \mathbf{x}$
$= (\mathbf{v}^T \mathbf{x})^T \mathbf{v}^T \mathbf{x} = \Vert \mathbf{v}^T \mathbf{x} \Vert_2^2 \geq 0$Leading Principal Minor
\(\begin{pmatrix} a_{1, 1} \end{pmatrix} \\ \begin{pmatrix} a_{1, 1} & a_{1, 2} \\ a_{2, 1} & a_{2, 2} \end{pmatrix} \\ \begin{pmatrix} a_{1, 1} & a_{1, 2} & a_{1, 3} \\ a_{2, 1} & a_{2, 2} & a_{2, 3} \\ a_{3, 1} & a_{3, 2} & a_{3, 3} \end{pmatrix} \\ \vdots\)$\text{All}(\lambda_i) \geq 0$ $\mathbf{v} \mathbf{v}^T$꼴로 변형 가능 Leading Principal Minor의
Determinant가 모두 양수
($ad-bc$)
2) Example
Quadratic Function Least-Squares Objective $f(x) = \frac{1}{2}\mathbf{x}^TP\mathbf{x} + \mathbf{q}^T\mathbf{x} + r$ $f(x) = \Vert A\mathbf{x} - b \Vert_2^2$ $\Vert A\mathbf{x} - b \Vert_2^2 = (A\mathbf{x} - b)^T(A\mathbf{x}-b)$
$= \mathbf{x}^TA^TA\mathbf{x} - 2b^TA\mathbf{x} + \vert b \vert ^2$
($\because A^TA$꼴)
Quadratic Over Linear Log-Sum-Exponential $f(x, y) = \frac{x^2}{y}, \qquad y > 0$ $f(x) = log \sum \limits_{k=1}^n e^{x_k}$
$\qquad \, = log(e^{x_1} + e^{x_2} + … + e^{x_n})$\(\nabla^2f(x, y) = \frac{2}{y^3} \begin{bmatrix} y \\ -x \end{bmatrix} \begin{bmatrix} y & -x \end{bmatrix}\) 증명은 PSD정의대로 $\mathbf{v}^T f(x) \mathbf{v}$가 항상 0보다
크거나 같을 수 밖에 없음을 이용.※ Smooth Max Function
log-sum-exp함수의 특징은 다음과 같다.
$f(x)=log(e^{x_1} + e^{x_2} + … + e^{x_n}) \approx log(e^{x_k}) = x_k$
($x_k = max(x_1, x_2, … ,x_n$))
즉, $max()$함수보다는 smooth하고 미분가능하게
Maximum을 찾을 수 있다.
\(\nabla f(x) = \frac{1}{\sum \limits_i^n e^{x_i}} \begin{bmatrix} e^{x_1} \\ e^{x_2} \\ \vdots \\ e^{x_n} \end{bmatrix} \rightarrow softmax function\)
3. Convex Preserving
1) Operation
1. Positive Weighted Sum 2. Composition With Affine Function $f_i(x)$가 Convex
$\Rightarrow f(x)$도 Convex
ⅰ. $f(x) = w_1f_1(x) + w_2f_2(x) + … + w_mf_m(x)$
ⅱ. $f(x) = \int w(y) f_0(x, y) dy$$f(x)$가 Convex
$\Rightarrow f(A\mathbf{x} + b)$도 Convex
(※ 순서주의: Affine후 Convex Function)Convex Preserving
ⅰ. Non-Negative Multiple
ⅱ. sum of convex function(ex. $Af(x)+b$는 Convex가 아닐 수도 있음)
(if $b < 0$)
3. General Composition 4. Vector Composition $g: \mathbb{R}^n \rightarrow \mathbb{R} \quad h: \mathbb{R} \rightarrow \mathbb{R}$ $g: \mathbb{R}^n \rightarrow \mathbb{R}^k \quad h: \mathbb{R}^k \rightarrow \mathbb{R}$ $f(x) = h(g(x))$ $f(x) = h(g(x)) = h(g_1(x), g_2(x), …, g_n(x))$ $f”(x) = h”(g(x))g’(x)^2 + h’(g(x))g”(x)$활용 $\nabla^2 f(x) = g’(x)^T \nabla^2 h(g(x)) g’(x) + \nabla h(g(x))^T g”(x)$
5. Pointwise Maximum(& Minimum) 6. Pointwise Supremum(& Infimum) $f(x)$가 Convex
$\Rightarrow \max(f_1(x), …, f_m(x))$도 Convex$f(x, y)$가 임의의 fixed y에 대해 Convex
$\Rightarrow g(x) = \sup \limits_{y \in A} f(x, y)$도 Convex※ Proof
$\theta g(x_1) + (1-\theta)g(x_2) = \sup \limits_{y \in A} \theta f(x_1, y) + \sup \limits_{y \in A} (1-\theta) f(x_2, y)$
$\qquad\qquad\qquad\qquad\qquad \geq \sup \limits_{y \in A}(\theta f(x_1, y) + (1-\theta)f(x_2, y))$
$\qquad\qquad\qquad\qquad\qquad \geq \sup \limits_{y \in A}(f(\theta x_1 + (1-\theta) x_2, y))$
$\qquad\qquad\qquad\qquad\qquad = g(\theta x_1 + (1- \theta)x_2)$
7. Perspective(사상) $f(x)$가 Convex $\Rightarrow g(x, t) = tf(\frac{x}{t})$가 Convex
$f:\mathbb{R}^n \rightarrow \mathbb{R} \qquad g:\mathbb{R}^{n+1} \rightarrow \mathbb{R}$
2) Example
1. Composition With Affine Function ⅰ. Log Barrier
$\quad f(x) = - \sum \limits_{i=1}^n \text{log}(b_i - a_i^T \mathbf{x})$
ⅱ. Norm of Affine
$\quad f(x) = \Vert A\mathbf{x} + b \Vert_p$
2. General Composition 3. Vector Composition ⅰ. Exp
$\quad g$가 Convex이면 $e^{g(x)}$도 Convex이다.
ⅱ. Constant Over Convex
$\quad g$가 Concave이고 Positive면 $\frac{1}{g(x)}$는 Convex이다ⅰ. Sum-Log
$\quad g_i$가 Concave고 Positive면 $\sum \limits_{i=1}^n log(g_i(x))$는 Concave다.
ⅱ. Log-Sum-Exp
$\quad g_i$가 Convex이면 $log(\sum \limits_{i=1}^n e^{g_i(x)})$도 Convex이다.
4. Pointwise Maximum(& Minimum) 5. Pointwise Supremum(& Infimum) ⅰ. Piecewise Linear
$\quad f(x) = \max \limits_{i=1, …, m} (a_i^T \mathbf{x} + b_i)$
ⅱ. Largest Components
$\quad f(x) = \mathbf{x}[1] + \mathbf{x}[2] + … \mathbf{x}[m]$
$\quad (\mathbf{x}[1] < \mathbf{x}[2] < … < \mathbf{x}[m])$ⅰ. Not Convex($f$) Example
$\quad g(x) = \sup \limits_y x^2 \text{log}(1+y)$
ⅱ. Maximum Eigenvalues(RayReiguotient)
$\quad g(A) = \sup \limits_\mathbf{x} \frac{\mathbf{x}^T A \mathbf{x}}{\mathbf{x}^T \mathbf{x}} \quad f(\mathbf{x}, A) = \frac{\mathbf{x}^T A \mathbf{x}}{\mathbf{x}^T \mathbf{x}}$
ⅲ. Farthest Point
$\quad g(\mathbf{x}) = \sup \limits_{\mathbf{y} \in C} \Vert \mathbf{x} - \mathbf{y} \Vert$
4. Quasiconvex
어떤 함수는 Convex함수가 아니더라도 비슷한 역할을 할 수 있는 QuasiConvex함수일 수 있다.
1) 정의
$\mathcal{D}(f)$가 Convex이고 모든 $\alpha \in \mathbb{R}$에 대해서 $S_\alpha = \begin{Bmatrix}\mathbf{x} \in \mathcal{D}(f) | f(\mathbf{x}) \leq \alpha\end{Bmatrix}$가 Convex Set이면
f는 QuasiConvex이다.$\mathcal{D}(f)$가 Convex이고 모든 $\alpha \in \mathbb{R}$에 대해서 $S_\alpha = \begin{Bmatrix}\mathbf{x} \in \mathcal{D}(f) | f(\mathbf{x}) \geq \alpha\end{Bmatrix}$가 Convex Set이면
f는 QuasiConcave이다.Preserving
- Positive Weighted Maximum
- Infimum
※ Positive Weighted Sum은 Quasiconvex를 Preserving하지 않는다.
2) Example
Quasiconvex Quasiconcave Quasilinear ⅰ. $\sqrt{\vert x \vert}$
ⅱ. $f(x) = \frac{\Vert \mathbf{x} - a \Vert_2}{\Vert \mathbf{x} - b \Vert_2}$
$\quad (\mathcal{D}(f) = \begin{Bmatrix}\mathbf{x} | \Vert \mathbf{x}-a \Vert_2 \leq \Vert \mathbf{x} - b \Vert_2 \end{Bmatrix})$ⅰ. $f(x_1, x_2) = x_1x_2$
$\quad (\mathbf{x_1}, \mathbf{x_2} \in \mathbb{R}_{++}^n)$ⅰ. $\text{ceil}(x)$
ⅱ. $\text{log}(x)$
ⅲ. $f(x) = \frac{a^T\mathbf{x} + b}{c^T\mathbf{x} + d}$
$\quad (\mathcal{D}(f) = \begin{Bmatrix}\mathbf{x} | c^T\mathbf{x}+d >0\end{Bmatrix})$Proof
Quasiconvex Quasiconcave 1. $f(x_1, x_2) = x_1x_2$
$\quad (\mathbf{x_1}, \mathbf{x_2} \in \mathbb{R}_{++}^n)$\(x_1x_2 \leq \alpha \\ log(x_1 x_2) \leq log(\alpha) \\ log(x_1) + log(x_2) \leq log(\alpha) \\ \Rightarrow \text{not Quasiconvex}\)(Concave함수에서 어떤 값보다 작은부분) \(... \\ log(x_1) + log(x_2) \geq log(\alpha) \\ \Rightarrow Quasiconcave\)(Concave함수에서 어떤 값보다 큰 부분) 2. $f(x) = \frac{a^T\mathbf{x} + b}{c^T\mathbf{x} + d}$ \(\frac{a^T\mathbf{x} + b}{c^T\mathbf{x} + d} \leq \alpha \\ a^T\mathbf{x} + b \leq \alpha (c^T\mathbf{x} + d) \\ (a^T-\alpha c^T)\mathbf{x} \leq \alpha d - b \\ \Rightarrow Quasiconvex\) (Half Space꼴) \(... \\ (a^T-\alpha c^T)\mathbf{x} \geq \alpha d - b \\ \Rightarrow \text{Quasiconcave}\)(Half Space꼴) 3. $f(x) = \frac{\Vert \mathbf{x} - a \Vert_2}{\Vert \mathbf{x} - b \Vert_2}$ \(\frac{\Vert \mathbf{x} - a \Vert_2}{\Vert \mathbf{x} - b \Vert_2} \leq \alpha \\ \Vert \mathbf{x} - a \Vert_2^2 \leq \alpha^2 \Vert \mathbf{x} - b \Vert_2^2 \\ (1-\alpha^2) \Vert \mathbf{x} \Vert^2 + □ \\ \quad \\ if) \; \mathcal{D}(f) = \begin{Bmatrix}\mathbf{x} | \Vert \mathbf{x}-a \Vert_2 \leq \Vert \mathbf{x} - b \Vert_2 \end{Bmatrix} \\ \Rightarrow Quasiconvex\)(계수가 양수인 Quadratic Form)
5. Log Concave
어떤 함수는 Convex함수가 아니더라도 Log를 씌울 경우 Convex함수가 될 수 있다.
1) 정의
$f(\theta x_1 + (1-\theta) x_2) \geq f(x_1)^\theta f(x_2)^{1-\theta}$
가 성립할 경우 Log Concave이다.
Condition
\[f(x) \nabla^2 f(x) \preccurlyeq \nabla f(x) \nabla f(x)^T\]★ Log-Convex $\Rightarrow$ Convex $\Rightarrow$ Quasi-Convex
★ Concave $\Rightarrow$ Log-Concave $\Rightarrow$ Quasi-ConcavePreserving
- Product of Log Concave
- integration
- Convolution
※ Sum of Log Concave는 Log-Concave를 Preserving하지 않는다
2) Example
Log-Convex Log-Concave ⅰ. $x^a \quad a \geq 0$ ⅰ. $x^a \quad a \leq 0$
ⅱ. $\Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{u^2}{2}} du$Proof
Proof 1. Logistic Function
$\quad f(x) = \frac{e^x}{1+e^x}$\(log(f(x)) = log(e^x) - log(1+e^x) = x - log(1+e^x) \\ \nabla^2 log(f(x)) = \frac{-e^x}{(1+e^x)^2} < 0 \\ \Rightarrow \text{log-concave}\) 2. Harmonic Mean
$\quad f(x) = \frac{1}{\sum_{i=1}^n x_i^{-1}}$\(log(f(x)) = -log(\sum \limits_{i=1}^n x_i^{-1}) = -log(\sum \limits_{i=1}^n e^{-log(x_i)}) \\ = h(g(x)) \qquad (h(x): \text{log-sum-exp}, \quad g(x):-log(x)) \\ \Rightarrow \text{log-concave}\) 3. Product Over Sum
$\quad f(x) = \frac{\prod_{i=1}^n x_i}{\sum_{i=1}^n x_i}$