4. CSP

Constraint Satisfaction Problem

1. Background

1) 목표

Domain Specific한 Heuristic Function이 아닌 General 한 Heuristic Function으로 문제를 해결하는 것

2) 구성요소

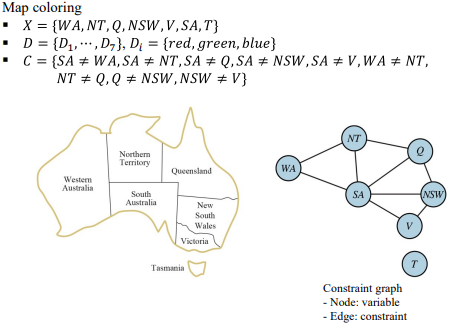
$\mathcal{X}$	변수	$\begin{Bmatrix}X_1 & X_2 & … & X_n \end{Bmatrix}$
$\mathcal{D}$	Domain 변수마다 각각의 Domain이 존재함	$\begin{Bmatrix}D_1 & D_2 & … & D_n \end{Bmatrix}$
$\mathcal{C}$	변수들이 갖는 Constraint 　ⅰ. unary Constraint: 변수가 1개인 constraint 　ⅱ. Binary Constraint: 변수가 2개인 Constraint	<범위, 관계>의 형태 ex. $\langle(X_1, X_2), \begin{Bmatrix}(3, 1), (3, 2), (2, 1) \end{Bmatrix} \rangle$ $\langle(X_1, X_2), X_1 > X_2 \rangle$

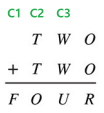
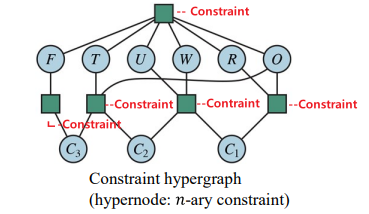
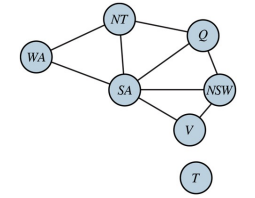
3) Constraint hypergraph

	1. 이와 같은 문제가 있다. 이 문제는 다음과 같이 표현할 수 있다. $alldiff(T, W, O, F, U, R)$ $\langle O+O = R+10\cdot C_1 \rangle$ $\langle C_1 + W + W = U + 10 \cdot C_2 \rangle$ $\langle C_2 + T + T = O + 10 \cdot C_3 \rangle$ $\langle C_3 = F \rangle$ $F \neq 0$
	2. 이 문제는 다시 Constraint Graph로 그릴 수 있다.

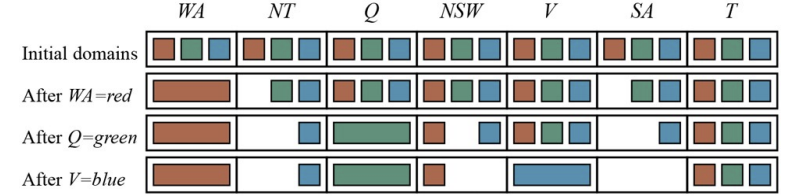
2. Constraint Propagation

위와 같이 문제를 모델링한 후에, 변수 하나에 임의의 값을 설정해보자.
그러면 Constraint에 의해 다른 변수들이 가질 수 있는 값에 영향이 간다.

이때, 이 영향은 Constraint에 직접적으로 참여하는 변수 뿐만 아니라 간접적으로 참여하는 변수도 포함이다. 이를 Constraint Propagation이라 한다.

1) Arc Consistency Enforcing

• Arc consistent
  

  Consistent Propagation을 위해서는 변수 $X$의 정의역의 모든값이 이 Constraint에 참여하게 해야한다. 이를 Arc consistent한 상태라고 정의한다.

(Domain에서 필요없는 Value가 없는 상태)

---

Algorithm

Arc Consistency를 만드는 알고리즘 중에서 AC-3라는 알고리즘이 있다.

이 알고리즘은 구현하기 쉽지만 다음과 같은 단점이 있다.

• Binary Constraint에 최적화 되어 있음
• 제약조건을 여러번 반복 점검하게 됨
• $cd^3$의 Time Complexity
  $c$: len(constraint)
  $d$: len(domain)

def AC_3(csp):
  q = queue([csp])
  while not q.is_empty():
      x1, x2 = q.pop()
      if REVISE(csp, x1, x2):
          if x1.domain.is_empty():
              return False
          # x1의 Domain이 줄었기 때문에 x1과 연결된 변수에 대해서 다시한번 Constraint 확인
          for x3 in x1.neighbors:
              if x3 == x2: continue
              q.append([x3, x1])

def REVISE(csp, x1, x2):
  revised = False
  for d in x1.domain:
      # x1, x2가 csp관계에서 가질수 있는 모든 원소들에 d가 있는지 확인
      if d not in all_element(csp, x1, x2)[0] 
          del x1[x1.find(d)]
          revised = True
  return revised

---

K-Consistency

K Consistency
(K=1) Node Consistency	어떤 변수가 자신에 속한 모든 Domain을 가질 수 있을 때
(K=2) Arc Consistency	두 변수에 대해서 일관성이 존재할 때	$\begin{Bmatrix}X_i, X_j\end{Bmatrix} x_i \leftrightarrow x_j$
(K=3) Path Consistency	세 변수에 대해서 일관성이 존재할 때 (3변수가 각각 다른 변수에 대해 Binary Constraint 존재)	$\begin{Bmatrix}X_i, X_j\end{Bmatrix} \qquad \; x_j$ $\begin{Bmatrix}X_j, X_k\end{Bmatrix} \quad \swarrow \;\uparrow$ $\begin{Bmatrix}X_k, X_j\end{Bmatrix} xi \rightarrow x_k$
(Strong) K Consitency	$(K=1, K=2, … , K=k)$를 모두 만족할 때 Strong K Consistency문제의 시간복잡도 = $O(n^2d)$ 그러나 Strong K Consistency로 만드는 게 NP-Complete이다.

2) Backtracking Search

def Backtracking_Search(csp):
    return _Backtracking_Search(csp, {})

def _Backtracking_Search(csp, assignment):
    if all([var in assignment for var in csp.var]):
        return assignment
    
    var = SELECT_VARIABLE([var not in assignment for var in csp.var])
    for value in SELECT_DOMAIN(var, assignment):
        if csp.consistent(var, value):
            assignment.append({var: value})
            inference = INFERENCE(csp, var, assignment)
            if inference != False:
                assignment.append(inference)
                result = _Backtracking_Search(csp, assignment)
                if result != False:
                    return result
                del csp[csp.find(inference)]
            del assignment[assignment.find(var)]
    return False

---

함수	방법1	방법2
SELECT_VARIABLE	- MRV(Minimum Remaining Value) 　: 가장 제약된 변수, 　실패할 가능성이 제일 큰 변수를 선택	- Degree Heuristic 　: 변수가 관여하는 제약의 개수가 　많은것부터 선택하는 방식 　(주로 처음 시작할 때 사용)
SELECT_DOMAIN	- Least Constraining Value : 변수에 값 $x$를 대입했을 때, 　다음Node들의 선택권이 많아지도록 선택
IFERENCE (실패가능성파악)	- Foward Checking 　: 값을 할당한 후에, 나머지의 Domain 수정 　Domain에 남은값이 없으면 삭제 후 재할당	- MAC(Maintain Arc Consistency) 　:값을 할당한 후 AC-3를 통해 　Arc Consistency확인 　(실패 가능성 미리 확인)
Back Tracking	- Back Jumping 　: 원인이 되는 부분까지 Jump 　(Q=빨, NSW=초, V=파, T=빨, SW=? 　T가 아닌 V가 문제임 $\rightarrow$ T를 건너뜀)	- Conflict-directed backjumping 　: 원인이 되는 부분이 복합적일 때 　(WA=빨, NSW=빨, T=빨, 나머지=? 　T가 아니라 WA와 NSW가 문제임)