2. CNN
1. BackGround
1) Data
위의 두 말은 다른 말일까??
자세히 보면 오른쪽 말 사진은 왼쪽 사진에서 잘라낸 사진이므로 같은 말임을 알 수 있다.하지만 CNN이 아닌 Fully Connected Layer로만 구성된 딥러닝 모델들은 이미지를 Flatten하고 Network에 넣기 때문에 다음과 같은 문제가 발생한다.
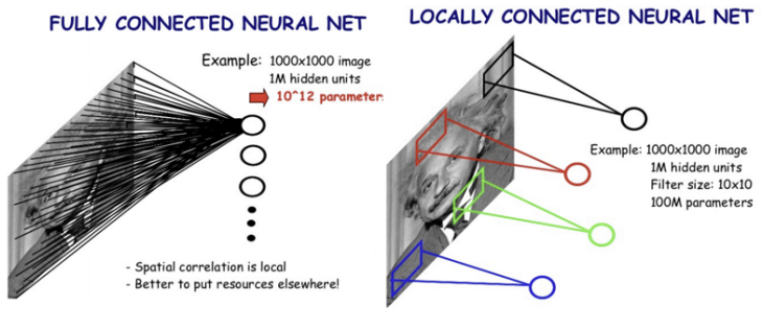
- 위치 정보 학습 불가능(픽셀이 조금만 바뀌어도 결과가 달라짐)
- 파라미터가 너무 많다.
따라서 우리는 이미지 데이터를 해석할 만한 다른 방법이 필요하다.
2) Convolution
Continuous Domain
- $x(t) * h(t) = \int^{\infty}_{-\infty} x(\tau)h(t-\tau)d\tau$
Discrete Domain
- $x[n]*h[n] = \sum\limits_{k=-\infty}^{\infty} x[k]h[n-k]$
우리는 위의 문제를 Convolution연산을 통해서 해결해 볼 수 있다.
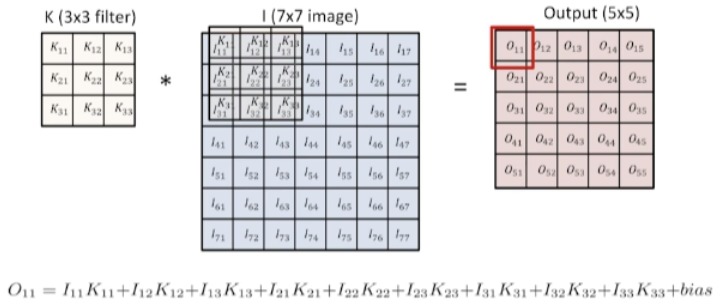
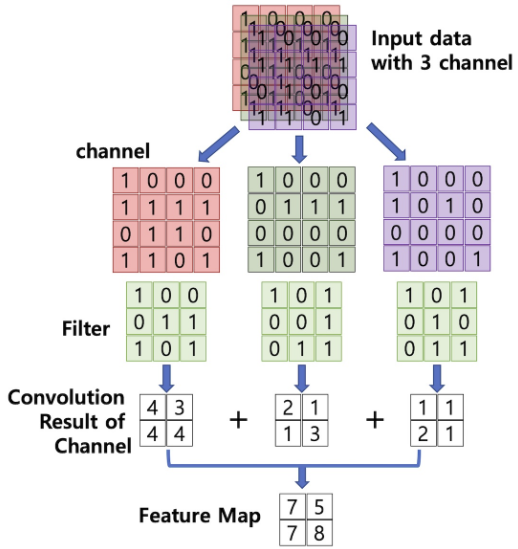
이 Convolution연산의 의미를 알아보기 전에 먼저 행렬에서 Convolution의 계산 방법부터 알아보자.
1-Channel 3-Channel (위 그림은
Padding_size=0,Stride=1인 경우이다.)1. Paddding
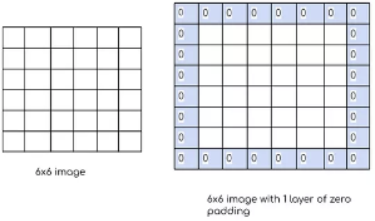
Convolution연산을 잘 살펴보면 행렬의 가장자리에 있는 데이터의 정보는 그렇지 않은 데이터에 비해 연산에 참여하는 횟수가 적다는 것을 확인할 수 있다.
즉, 가장자리데이터의 정보가 비교적 덜 중요하게 처리된다는 것이다.
이를 방지하기 위해 가장자리에 임의의 데이터를 추가적으로 채워 넣어주는 것을 Padding이라고 한다.
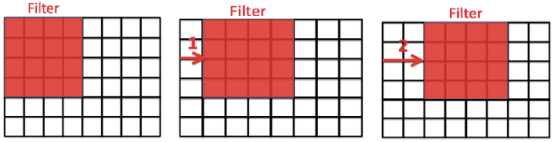
2. Stride
Stride는 filter가 Convolution 연산 후 이동하는 거리를 의미한다.
row, column방향 모두 Stride설정이 가능하다.AlexNet의 경우에는 Spatial Complexity를 줄이기 위해 이 Stride를 사용하였다.
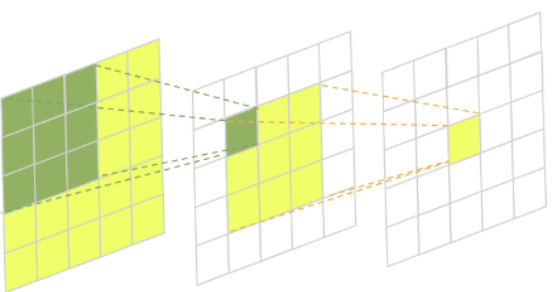
3. Receptive Field
Layer를 여러개 쌓을 때 결과 값에 대한 Input Data를 의미한다.
예를 들어, 위의 마지막 Layer의 노란색 Pixel에 대한 Receptive Field는 맨 처음 Layer의 전체 Data가 될 것이다.
이 Receptive Field의 개념은 추후 모델 Architecture의 변화를 설명할 때, 자주 사용되기 때문에 반드시 숙지해 놓자.
3) CNN
 |  |
Convolution연산은 자신의 패턴과 비슷한 부분을 찾아준다는 특징이 있다.
즉, 예를 들어 Max Pooling같은 경우는 자신의 패턴과 가장 비슷한 부분을 찾아준다.
예전에는 이러한 Kernel들을 전부 수작업으로 제작했었지만, CNN은 이 Kernel을 딥러닝을 통해서 찾는 과정이라고 생각할 수 있다.또한 Convolution연산을 통해 얻은 데이터는 연산 과정을 보면 알 수 있듯이 이미지 전체를 분석하기 보다는, “부분 이미지”를 분석한다.
즉, 전체적인 이미지에 대한 특징을 나타내는 Fully Connected Layer보다 해당 이미지를 해석하는데 도움이 된다.
이렇게 Convolution 연산을 활용하는 Layer로 구성된 Neural Network를 Convolutional Neural Network(CNN)이라고 한다.
활용
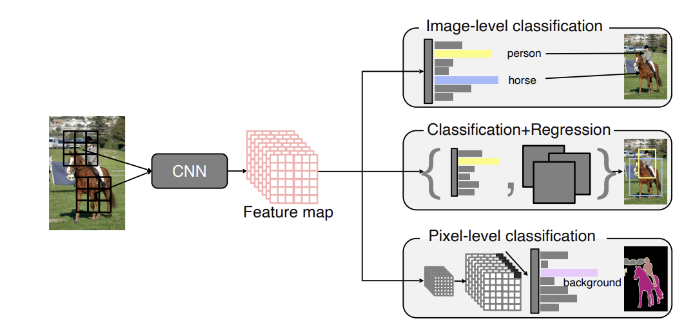
CNN을 활용한 이미지 분류 Task는 크게 다음과 같이 나눠 볼 수 있다.
- Classification
- 어떤 이미지에 대해 그 이미지가 어떤 Label에 속하는 이미지인지 판별하는 문제
- Detection
- 이미지의 어떤 부분이 내가 원하는 Label에 속하고 있는지 찾아내는 문제
- Segmentation
- 이미지를 Pixel단위로 Classification하는 문제
4) Components
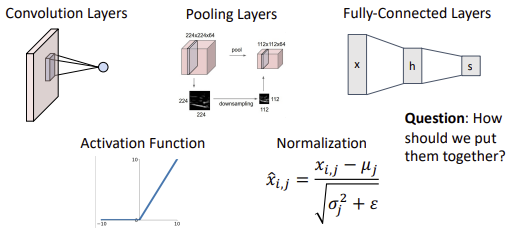
CNN에는 Convolution Layer뿐만아니라 다양한 구성요소들이 복합적으로 존재한다.
따라서 이 요소들을 어떻게 조합하면 우리가 하고자 하는 Task에 최적의 Architecture를 만들 수 있는지 아는 것이 중요하다.
- Convolution Layer
- for feature extract
- Pooling Layers
- Down Sampling
- Fully Connected Layer
- for classification
- Activation Function
- ReLU, Sigmoid, tanh, …
- Normalization
- $\hat{x}_{i, j}$– $= \frac{x_i - \mu_j}{\sqrt{\sigma^2_j + \epsilon}}$
2. Architecture
1) Preview
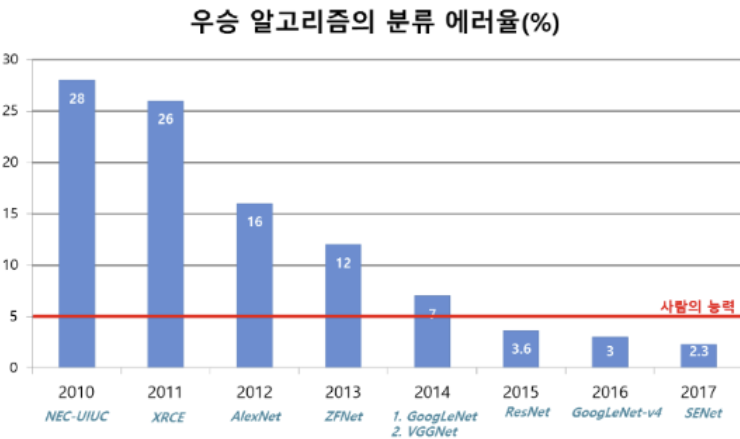
여기서는 Imagnet Large Scale Visual Recognition Challenge(이미지넷 이미지 인식 대회) 이하 ILSVRC에서의 우승 모델들에 대해 알아보면서 CNN기반 Model들의 발전과정과 어떤 방향으로 발전할 것인지 알아보고자 한다.
CNN Architecture들은 주로
Convolution Layer,Pooling Layer,Fully Connected Layer로 이루어져있다.이때, 초기 모델들의 발전과정을 잘 살펴 보면
Fully Connected Layer의 크기를 줄이는 방향으로 점점 바뀌게 된다는 것을 확인할 수 있다.이 이유는 Parameter의 수가 늘어나면 늘어날수록 학습이 어렵고, Generalization성능이 줄어드는데,
Fully Connected Layer는 그 특성상 매우 많은 수의 Parameter를 갖기 때문이다.단, 그렇다고 Parameter수가 적은 것이 좋다는 것은 아니다.
이는 Model의 Capacity와도 연관이 있기 때문인데, 따라서 후기 모델들은 이를 Architecture 설계를 통해 극복해 나가고 있다.
Parameter $\Uparrow$ Parameter $\Downarrow$ Capacity $\uparrow$ (good) $\downarrow$ (bad) Accuracy $\uparrow$ (good) $\downarrow$ (bad) Complexity $\uparrow$ (bad) $\downarrow$ (good) Overfitting $\uparrow$ (bad) $\downarrow$ (good) Generalization $\downarrow$ (bad) $\uparrow$ (good) 즉, 위와 같은 Trade Off가 존재하기 때문에 이를 고려한 Architecture 설계가 필요하다.
또 모델 Architecture를 분석하기 위해 Memory usage나 Parameter 개수, Flops를 계산할 수 있어야 한다.
- Convolution Output Size
- $W_{out} = \lfloor \frac{W-K_w+2P_w}{S_w} + 1 \rfloor$
- $H_{out} = \lfloor \frac{H-K_h+2P_h}{S_h} + 1 \rfloor$
- Memory Usage
- $Memory = \frac{Output Size \times 자료형크기}{1024}[KB]$
- Output Size = $C_{out} \times W_{out} \times H_{out}$
- 자료형 크기 = 4 (32-bit floating point)
- Learnable Params
- $Params = C_{out} \times C_{in} \times K_w \times K_h + C_{out}$
- $C_{out} =$ Kernel의 개수 = Output Channel의 수
- $C_{in} =$ Kenel의 Channel수 = Input Channel의 수
- Number Of Flops: 곱셈연산 개수
- $Flops = OutputSize \times KernelSize \times C_{in}$
- Output Size = $C_{out} \times W_{out} \times H_{out}$
- Kernel Size = $K_{w} \times K_{h}$
(FLOPS= Floating Point Operations Per Second)
2) 2012-AlexNet
AlexNet은 2012년도 ILSVRC 우승 논문으로,
처음으로 딥러닝 방식을 통해 기존 알고리즘들을 이기고 우승을 차지했다.
이 논문 이후로는 모두 딥러닝방식들이 ILSVRC에서 우승하게 된다.따라서, AlexNet은 현재 딥러닝 모델들의 기본적인 틀을 만들었다는 평가를 받고 있다.
주요 특징
- 2개의 GPU사용
- 당시에는 GPU성능/용량이 좋지 않았기 때문에 2개의 3GB GPU에 나누어 학습하도록 구성함
- Local Response Normalization(LRN)
- 현재는 잘 사용하지 않는 기법이지만 AlexNet에서는 이 LRN을 처음으로 사용함
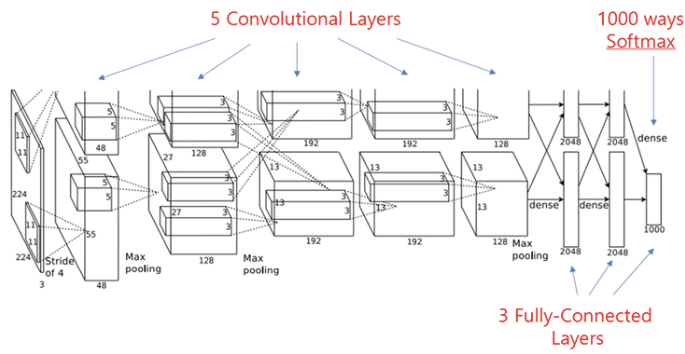
- CL: 5개, FCL: 3개
- 11, 5, 3 크기의 Convolution Kernel을 사용
ReLU사용
- DropOut 사용
- 깊어진 Network에서 과적합 방지를 위해 사용
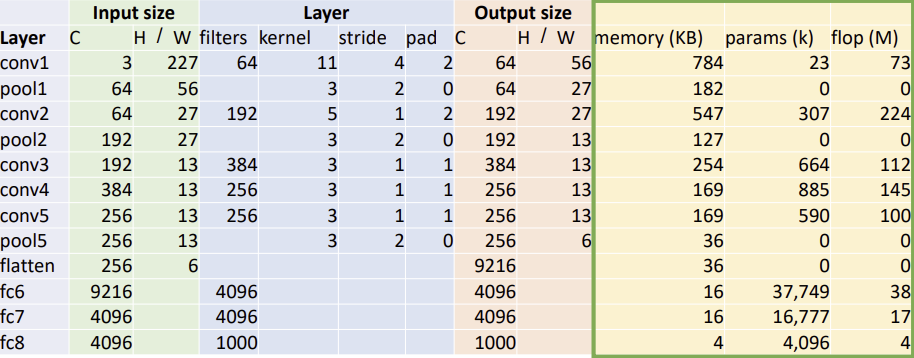
Layer별 분석
(Pooling Layer에는 Learnable Parameter가 없다.)
(ReLU는 각 Convolution Layer 바로 뒤에 존재한다.)
Memory Usage Parameter FLOP 주된 사용 위치 앞 뒤(FC Layer) 중간 문제점
- 뒤의 FC Layer가 너무 많은 Parameter를 갖는다.
- 정확도를 높인 대신 Complexity가 매우 증가했다
(Parameter수 $\uparrow$, Memory Usage $\uparrow$)- 사용 가능한 Memory의 한계 때문에 Layer의 깊이에 한계가 있다.
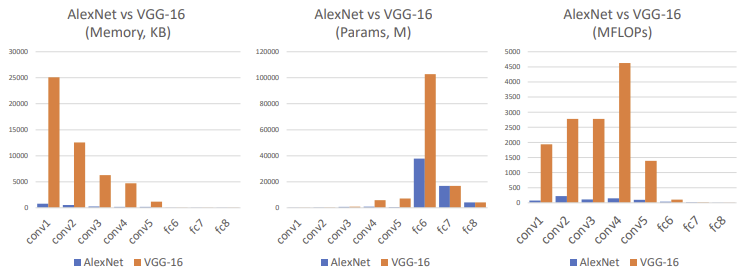
3) 2014-VGGNet
VGGNet은 2014년도 ILSVRC의 준우승 논문으로 우승논문은 아니지만, 후에 나올 딥러닝의 방향을 제시한 논문이다.
VGG는 Layer의 수에 따라 VGG16, VGG19로 나뉜다.
주요 특징
VGG는 다음과 같은 목표를 가지고 Design되었다.
- Simple(Regular) Design
- Convolution = $(3 \times 3), 1S, 1P$
- Max Pool = $(2 \times 2), 2S$
- Doubling Channels after pool
- Deeper Network
- Stage1:
Conv-Conv-Pool- Stage2:
Conv-Conv-Pool- Stage3:
Conv-Conv-Pool- Stage4:
Conv-Conv-Conv-Pool- Stage5:
Conv-Conv-Conv-Pool즉, 오직 $3 \times 3$ 의 작은 Convolution Filter만을 사용하여 깊은 Layer를 구성하였다.
(참고)
Fully Connected Layer에1x1Convolution filter사용하였지만, 이것은 Parameter의 수를 줄이고자 한 것은 아니었다고 한다.3x3 Convolution의 특징
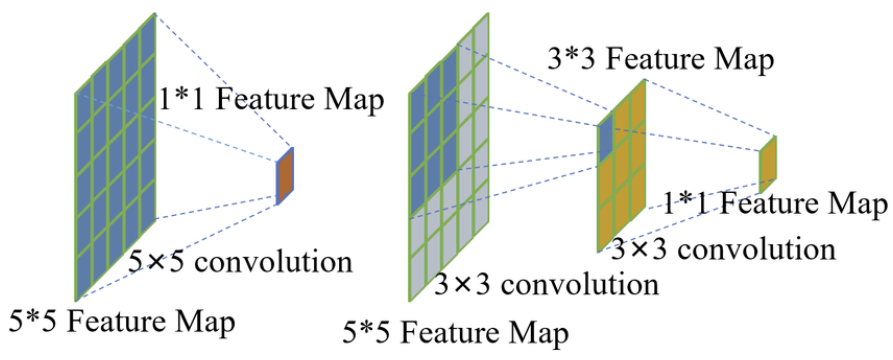
$3 \times 3$ Convolution을 2개 사용하는 것과
$5 \times 5$ Convolution을 1개 사용하는 것의 차이를 살펴보자.우선, 두 연산의 Receptive Field의 크기는 $5 \times 5$로 갖다.
반면에 Parameter와 Flops에 있어서 차이가 존재하는데 이를 계산해 보자.
- $5 \times 5$ Convolution
- Parameter: $5^2 \times C_{in} \times C_{out}$
- Flops: $5^2 \times C_{in} \times OutputSize$
- $3 \times 3$ Convolution
- Parameter: $(3^2+3^2) \times C_{in} \times C_{out}$
- Flops: $(3^2+3^2) \times C_{in} \times OutputSize$
즉, $3 \times 3$ Convolution을 사용하는 것이 다음과 같은 측면에서 좋다는 것을 알 수 있다.
- Complexity를 낮출 수 있다.
(연산량과 Parameter모두 낮춘다)- Non-Linear Activation Function을 많이 사용할 수 있다.
Doubling Channels
$3 \times 3$ Convolution을 사용하는 것이 연산량과 메모리 사용을 낮추어 준다는 측면에서 이득을 볼 수 있었다.
하지만, 이것이 $3 \times 3$ Convolution을 사용하는 것이 항상 좋다것을 의미하지는 않다.
Parameter가 줄어든다는 것은 Network의 Capacity가 줄어든다는 것이기 때문이다.
이를 보완하기 위해 VGG는 Pooling Layer이후에 Convolution과정에서 Channel을 Doubling해주어 Network에 충분한 Capacity를 보장해주고자 했다.
4) 2014-GoogleNet
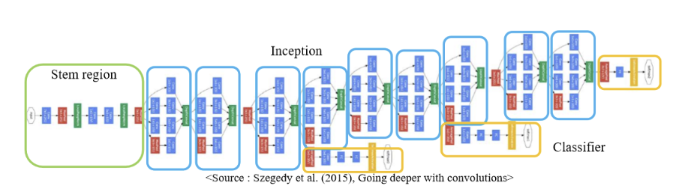
2014년도 ILSVRC 우승 논문
GoogleNet은 2014년도 ILSVRC우승 논문으로 Inception Block을 통해 parameter수를 매우 적게 사용하여 좋은 성능을 낸 Architecture이다.
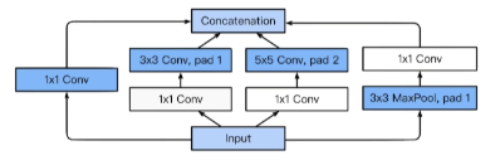
Inception Block
하나의 입력에 대해 여러 결과를 만들고 이를 Concatenate한다.
$1 \times 1$ Convolution을 활용해 Parameter의 수를 매우 줄였다.
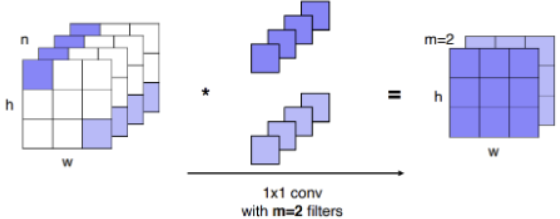
$1 \times 1$ Convolution
위의 그림을 보면 알 수 있듯이 $1 \times 1$ Convolution은 Channel의 깊이를 줄이는 역할을 한다.
즉, layer중간중간 이 $1 \times 1$ Convolution를 잘 활용할 경우 Parameter의 수를 줄이는데 매우 효과적이다.
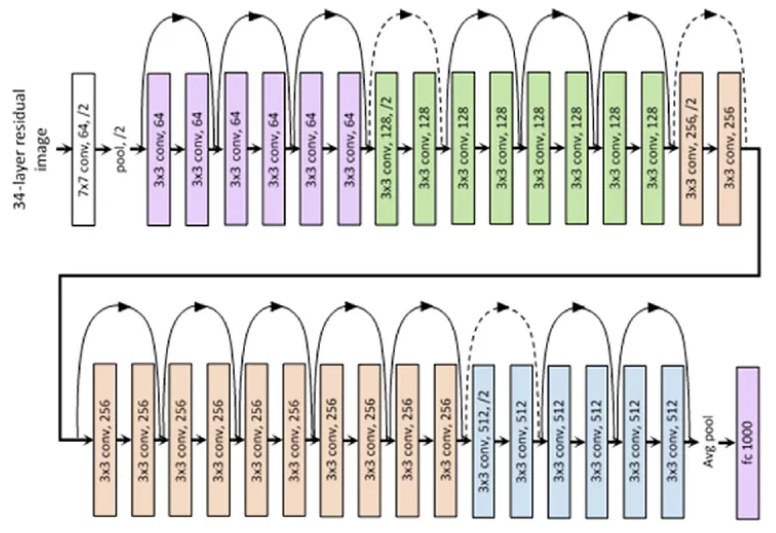
5) 2015-ResNet
2015년도 ILSVRC 우승논문으로 Kaiming He가 고안한 Architecture이다.
이전까지는 모델의 깊이가 깊어지면 오히려 성능이 안좋아 진다는 단점이 있었지만,
Resnet은 Residual Connection을 통해 이를 해결해 처음으로 사람의 능력을 이기는 모델을 만들었다.주요 특징
ⅰ. Residual Block
ⅱ. Skip Connection
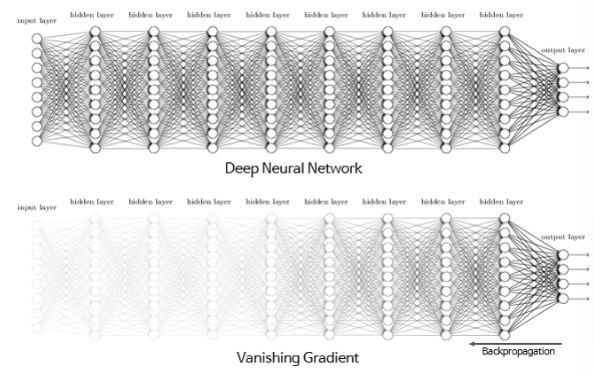
ⅲ. Bottleneck Architecture사용Gradient Vanishing Problem
처음 DeepLearning이 나왔을 때는 Layer가 어느정도 이상 깊어지면 오히려 Over fitting이 발생해 성능이 떨어진다고 생각했다.
하지만, Training Error도 전반적으로 얕은 모델들보다 컸기 때문에 이 이유는 기각된다.
즉, Over fitting이 아닌 Under fitting되었던 것이었다.이러한 Under fitting은 Deeper model이 Shallow model과 같이 학습할 경우 Extra layer에 대한 학습이 잘 되지 않기 때문에 발생한다.
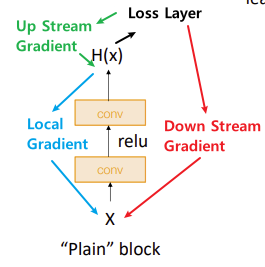
이는, Chain Rule을 활용한 Gradient Descent 방식으로 학습할 때, Local Gradient가 활성화 함수로 인해 사라지기 때문이다.
($\because 0 < \nabla Sigmoid, \nabla tanh < 1$)이 전까지는 이 문제를 해결하기 위해서 주로 배치 정규화나 (Leaky)ReLU 와 같이 기울기가 1인 활성화 함수를 활용했지만 여전히 문제가 발생하였다.
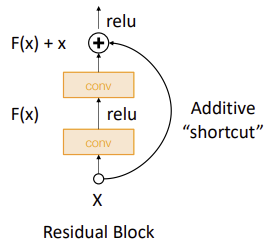
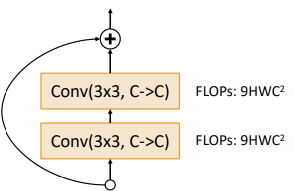
1. Residual Block
Plain Block Residual Block 그림 Chain Rule $\frac{\partial L}{\partial x} = \frac{\partial L}{\partial H(x)} \times \frac{\partial H(x)}{\partial x}$
$\&\quad 0\leq \frac{\partial H(x)}{\partial x} \leq 1$$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial H(x)} \times \frac{\partial (F(x)+x)}{\partial x}$
$\&\quad \frac{\partial (F(x)+x)}{\partial x} \geq 1$Identity Mapping $H(x) = x$ $F(x) + x = x$ Residual Block은 위와 같이 Local Gradient가 소실되는 것을 막는 것 뿐만 아니라 이를 통해 Identity Mapping도 잘 적용할 수 있었다.
이는, 추가적인 Layer를 쌓는다고 하더라도, 모든 Convolution Block의 weight를 0으로 만들고 시작하면($F(x)=0$) identity mapping function은 $x=x$이므로 쉽게 구현할 수 있기 때문이다.
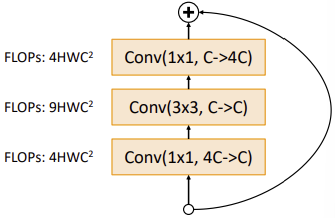
2. Bottleneck Block
Plain Block Bottleneck Block 그림 FLOPs $18HWC^2$ $17HWC^2$ Layer $2$ $3$ 앞에서 살펴보았듯이 Convolution은 전체 Channel에 대해서 동작한다.
따라서 Channel을 줄인 후에 Convolution을 수행하면 연산량을 줄일 수 있을 것이라는 Idea를 바탕으로 만들어진 Block이다.Bottleneck Block은 $1 \times 1$ Convolution Block을 활용하여 Channel을 $\frac{1}{4}$ 로 줄이고
Convolution을 계산한 후 다시 원래 Channel로 바꿔주는 방식으로 설계되었다.3. 구조
Stage
ⅰ. Regular Design: $3 \times 3$ Convolution Block만 사용을 사용하여 Stage를 구성했다.
ⅱ. Hierarchical Design: 각 Stage의 첫번째 Block은 Resolution($H \times W$)를 절반으로 줄이고 채널을 2배로 늘린다.
- Stem Layer
- 초반에 Spatial Complexity가 많은것을 극복하기 위해 $7 \times 7, 2S, 3P$ Convolution과 $3 \times 3, 2S, 1P$ Max Pooling을 사용하여 Input Size를 줄여주었다.
- GAP(Global Average Pooling)
- 대부분의 파라미터가 마지막에 존재하는 것을 극복하기 위해
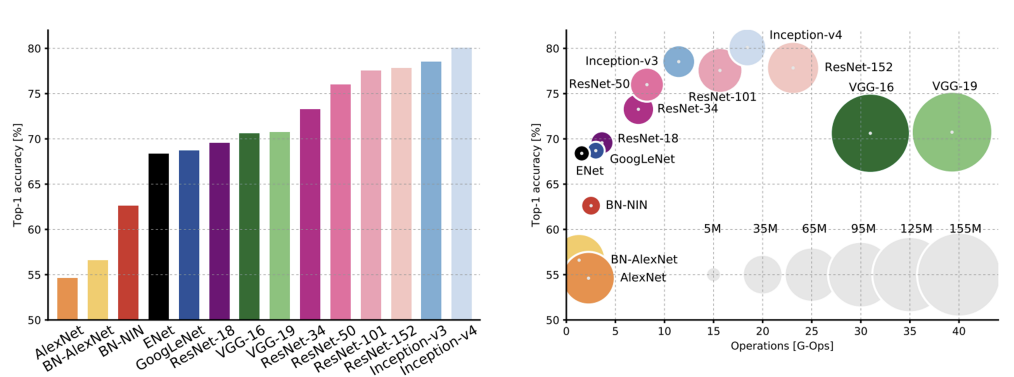
Fully connected Layer대신에 Global Average Pooling을 사용하였다.성능 비교
6) 2017-DenseNet
마지막으로, ILSVRC우승 논문은 아니지만, CVPR에서 2017년도에 Best Paper를 받은 “Densely Connected Convolutional Networks”에 대해 알아보자.
주요 특징
ⅰ. Dense Block을 사용
ⅱ. Transition Block을 사용
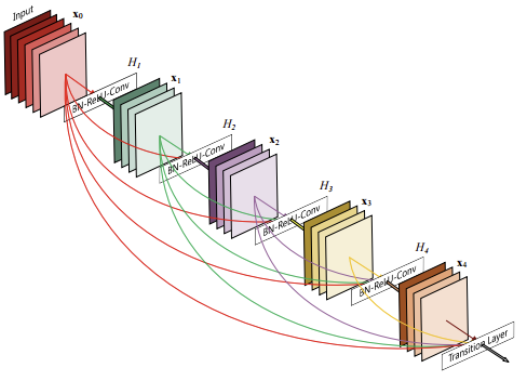
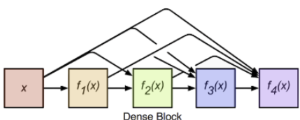
ⅲ. Bottleneck Architecture사용1. Dense Block
Dense Block의 큰 특징은 다음 두가지와 같다.
ⅰ. Skip Connection ⅱ. Concatenation 그림 특징 Feed Forward시 각 Layer들을 다른 모든 Layer들과 연결한다. Resnet에서 사용하는 Addition대신
Concatenation을 활용한다.이유 - Vanishing-Gradient 문제를 완화할 수 있다.
- Feature Propagation을 강화할 수 있다.
- Feature를 대사용할 수 있다.
- Paramenter의 수를 줄일 수 있다.- Resnet에서 사용하는 Addition방법은
계산량의 증폭으로 정보의 흐름을 지연시킨다.2. Transition Block
DenseBlock을 지날 경우 Concatenate연산에 의해 그 Output의 크기가 매우 커진다.
이를 해결하기 위해 위의 그림처럼 중간중간마다 Transition Block을 활용해 주었다.Transition Block은 $1 \times 1$ Convolution과 Pooling작업을 통해 커진 Output을 다시 알맞은 크기로 변형시켜주는 역할을 한다.
.png)
-Todo-