1. Basic Algorithm & Ancient Cipher

Basic Algorithm

1. Modulo 연산

1) 정의

$\frac{A}{B} = Q$와 나머지 $R$을 가질 때, $A \bmod B = R$이다.

• (합동) $A \equiv B \pmod C$
  

  모듈로 연산 $C$ 에서 같은 값을 갖게 되는 수들($A, B$)을 모듈로 $C$에 대한 합동 관계에 있다고 한다.

• (덧셈의 역원) $A + B \equiv 0 \pmod m$
  

  Modulo $m$에서 두 수의 합이 0과 합동일 때, 두 수는 modulo $m$에서 덧셈 역원이라고 한다.

• (곱셈의 역원) $A \times B \equiv 1 \pmod m$
  

  Modulo $m$에서 두 수의 곱이 1과 합동일 때, 두 수는 modulo $m$에서 곱셈 역원이라고 한다.

2) 성질

Modulo 성질

• (덧셈): $(A + B) \bmod C = (A \bmod C + B \bmod C) \bmod C$
• (곱셈): $(A \times B) \bmod C = (A \bmod C \times B \bmod C) \bmod C$
• (제곱): $A^B \bmod C = ((A \bmod C)^B) \bmod C$

---

Modulo 합동 성질

• 전달성
  (가정) $a \equiv b \pmod m$ 이고 $b \equiv c \pmod m$
  (결과) $a \equiv c \pmod m$

• 곱셈
  (가정) $a \equiv b \pmod m$
  (결과) $ac \equiv bc \pmod m$

• 나눗셈
  (가정) $ac \equiv bc \pmod m$ 이고 $\gcd(c, m) = 1$
  (결과) $a \equiv b \pmod m$

• CRT
  (가정) $a \equiv b \pmod p$ 이고 $a \equiv b \pmod q$ 이고 $\gcd(p, q) = 1$
  (결과) $a \equiv b \pmod pq$

---

예제

\[c = m^e \bmod n\]

$e = 10, n = 15, m = 3$ 일때, 위의 식을 만족하는 $c$를 구하라.

$e = 10 = [1, 0, 1, 0]]$

i	e	z
3	1	$1^2 \cdot 3 \bmod 15$
2	0	$3^2 \bmod 15$
1	1	$9^2 \cdot 3 \bmod 15$
0	0	$3^2 \bmod 15$

∴ 답: 15

2. 기타 공식들

1) Euclidean Algorithm(유클리드 호제법)

\[GCD(a, b) = GCD(b, r), \quad \text{where } a>b, a \equiv r \pmod b\]

최대 공약수 알고리즘

$GCD(252, 198)$
$= GCD(198, 54)$
$= GCD(54, 36)$
$= GCD(36, 18)$
$= 18$

---

기타 표기

• $Z_m = m-1$
  (e.g. $Z_{26} = 25$)

• $Z_m^\ast = [a | a \in Z_m \text{ and } \gcd(a, m) = 1 ]$
  , (e.g. $Z_{7} = [1, 3, 5]$)

2) Extended Euclidean Algorithm

$ax + by = \gcd(a, b)$를 만족하는 x, y가 존재하며, 이는 유클리드 호제법의 과정을 역으로 따라가면 찾을 수 있다.

Example

a = 252와 b = 198일 때 $ax + by = \gcd(a, b)$를 만족하는 x, y를 찾아라.

① $252 = 198 \times 1 + 54$
② $198 = 54 \times 3 + 36$
③ $54 = 36 \times 1 + 18$
④ $36 = 18 \times 2 + 0$
⑤ $54 - 36 \times 1=18$ …(from ③)
⑥ $54 - (198 - 54 \times 3) = 18$ …(from ②)
⑦ $4 \times 54 – 198 = 18$
⑧ $4 \times (252 - 198) - 198 = 18$ …(from ①)
⑨ $4 \times 252 - 5 \times 198 = 18$

역원 찾기 알고리즘

곱셈에 대한 역원은 이 Extended Euclidean Algorithm을 사용하면 쉽게 찾을 수 있다.

Example

(문제) 31과 $\bmod 105$에서 역원인 수를 구하여라.

$31 a + 105 b = \gcd(31, 105) = 1$을 만족하는 x, y를 찾아보자.

$-44 \times 31 + 13 \times 105 = 1$

이때, $(13 \times 105) \bmod 105 = 0$ 이므로,
$\bmod 105$에서 13과 곱셈에 대해 역원인 수는 $-44(\equiv 61 \bmod 105)$이다.

---

Ancient Cipher

Concept

• Symmetric Key Cipher
  

  $D_k(E_k(x)) = E_k(D_k(x)) = x$

• Kerchoff’s Principle
  

  항상 공격자가 암호화/복호화 알고리즘을 알고있다고 가정해야 하고, 오직 Key의 비밀성에 의해서만 암호의 내성을 평가해야 한다.

1. Transposition Cipher

1) Rail fence Cipher

plain text: “meet meat the park”

2) Permutation key Cipher

plain text: “enemy attac kston ightz”

cipher text: “eemyn taact tkons hitzg”

2. Substitution Cipher

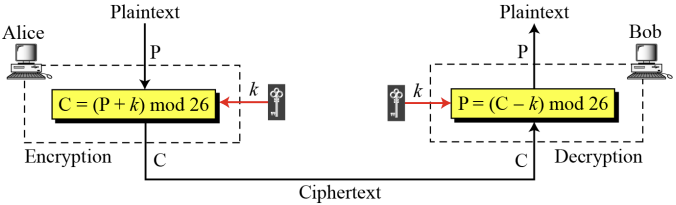
1) Additive Cipher

• monoalphabetic cipher

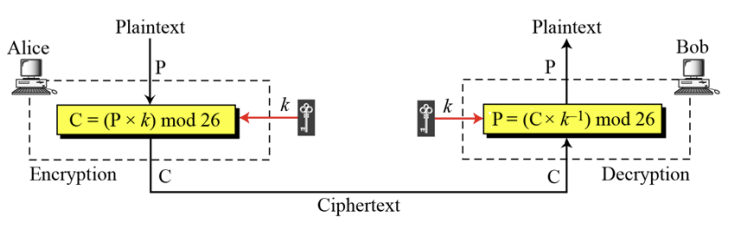
2) Multiplicative Cipher

• monoalphabetic cipher

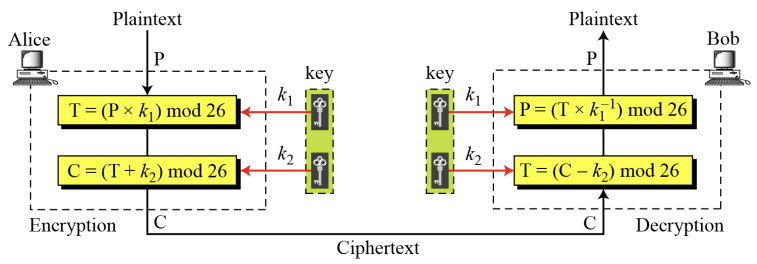
3) Affine Cipher

4) Permutation Cipher

• monoalphabetic cipher
• Frequency analysis

5) Vigenere Cipher