포스트

5. Algorithm

게시 업데이트
By UI-JIN KIM 14 분읽는 시간

1. Unconstrained Minimization

\[\text{Minimize: } f(\mathbf{x})\]

$\mathbf{x} \in \mathbb{R}^n,$
$f(\mathbf{x}) \text{는 Convex},$
$f(\mathbf{x}) \text{는 두번 미분 가능}$

Background

Minimization을 Algorithm으로 구현할 때의 핵심은 $f(x^{(n)}) = p^*$일 때, Iterative Method를 사용해 KKT Condition을 만족할 때 까지 $x^{(0)}, x^{(1)}, … , x^{(n)}$점으로 진행하는 것이다.

이때, Unconstrained문제이므로 이 최적점 $\mathbf{x}^{(n)}$는 결국 $\nabla f(\mathbf{x}^*) \approx 0$을 만족할 것이다.

이 점을 찾기 위해서 Descent Method를 사용할 수 있는데, 이 방법의 핵심은 다음과 같다.
먼저 Convex함수이기 때문에 항상 내려가는 방향으로 움직이기만 하면 된다.

\[\mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} + t^{(k)} \vartriangle \mathbf{x}^{(k)} \\ f(\mathbf{x}^{(k)}) > f(\mathbf{x}^{(k+1)})\]

$\vartriangle \mathbf{x}$는 방향
$t > 0$는 크기

즉, 위 식을 만족하는 $f(\mathbf{x}^{(k+1)})$을 찾아야 하는데, 이를 찾기 위해 다음의 사실을 이용할 수 있다.
$f(\mathbf{x}^{(k+1)}) > f(\mathbf{x}^{(k)}) + \nabla f(\mathbf{x}^k)(\mathbf{x}^{k+1} - \mathbf{x}^k) \rightarrow$ (Convex의 정의)

즉, 해당 지점에서의 미분값과 크기를 $\nabla f(\mathbf{x}^{(k)})^T \vartriangle \mathbf{x}^{(k)} < 0$를 만족하도록 정의하면 된다.

이제 이동할 크기(Learning Rate)를 정하는 방법을 먼저 살펴보자

Exact Line SearchBacktracking Line Search
$t = \text{arg} \min \limits_{t > 0} f(\mathbf{x} + t \vartriangle \mathbf{x})$$f(\mathbf{x} + t \vartriangle \mathbf{x}) < f(\mathbf{x}) + \alpha t \nabla f(\mathbf{x})^T \vartriangle \mathbf{x}$
t만큼 움직였을 때, 함수값이 가장 작아질 때현재위치에서 접선의 기울기보다
기울기의 절댓값을 줄인 직선보다
아래에 있을 때
t에 대해 Restriction to a line이기 때문에
Convex함수 이므로 Minimization문제를 푼다		alt text
ⅰ. $t=1, \alpha \in (0, \frac{1}{2}), \beta \in (0, 1)$로 Setting
ⅱ. $t = \beta t$를 위 식을 만족할 때 까지 반복
단점
: Convex문제를 풀어야하기 때문에 복잡도 $\Uparrow$		생각보다 성능이 좋다.

위에서는 learning rate들을 정할 수 있는 몇가지 방법을 알아보았으니 이제 방향 등 자세한 방식들을 알아보자.

1) Gradient Descent

$\mathbf{x}$에서 움직일 방향을 Gradient로 설정하는 방식이다.

\[\mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} + t^{(k)} \vartriangle \mathbf{x}^{(k)}\]
 Gradient DescentSteepest Descent
$\vartriangle x$$\vartriangle x = -\nabla f(\mathbf{x})$ⅰ. Normalized
$\quad \vartriangle x_{nsd} = \text{arg}\min \limits_{\Vert v \Vert_P \leq 1} (\nabla f(\mathbf{x})^T v)$
$\quad$(Gradient Descent의 일반화 ver)
$\quad$(v에 대한 Norm)

ⅱ. Unnormalized
\(\quad \vartriangle x_{sd} = \Vert \nabla f(\mathbf{x}) \Vert_* \vartriangle \mathbf{x}_{nsd}\)
$\,$
목표현재 기울기가 가장 가파른 곳으로 이동
Unnormalized Steepest Descent의
2-norm ver		$f(\mathbf{x} + v) \approx f(\mathbf{x}) + \nabla f(\mathbf{x})^Tv$
$v$만큼 움직였을 때
함숫값이 최소가 되도록
$\,$
해법현재 위치에서 Jacobian을 구한다.\(\text{Minimize} \qquad \nabla f(\mathbf{x})^T v \\ \text{Subject to} \qquad \Vert v \Vert_P \leq 1\)
문제 이므로 Convex Optimization 문제
 L1-NormEuclidean NormQuadratic Norm
$\vartriangle \mathbf{x}_{nsd}$ \(-\frac{\nabla f(\mathbf{x})}{\Vert \nabla f(\mathbf{x}) \Vert_2}\) 
$\vartriangle \mathbf{x}_{sd}$ \(\Vert \nabla f(\mathbf{x}) \Vert_2 \times -\frac{\nabla f(\mathbf{x})}{\Vert \nabla f(\mathbf{x}) \Vert_2}\)
\(\therefore - \nabla f(\mathbf{x})\)		\(\therefore -P^{-1}\nabla f(\mathbf{x})\)

Convergence rate

$f(\mathbf{x})$가 Strongly Convex일 경우 다음 식을 항상 만족한다.

\[f(\mathbf{x}^{(k)}) - p^* \leq c^k (f(\mathbf{x}^{(0)}) - p^*)\]

즉, Convergence가 보장된다.
(c가 작을수록 Convergence 속도는 느려짐)

※ Strongly Convex: $\nabla f(\mathbf{x}) - mI\succeq 0$
$\quad$(휘어짐의 정도(곡률)이 $mI$보다 큼)

Algorithm

1
2
3
4
5

while stop:
    x = now
    direction = -Gradent(f, x)
    step_size = Line_search(f, x, alpha, beta)
    now = x + step_size * direction

단점

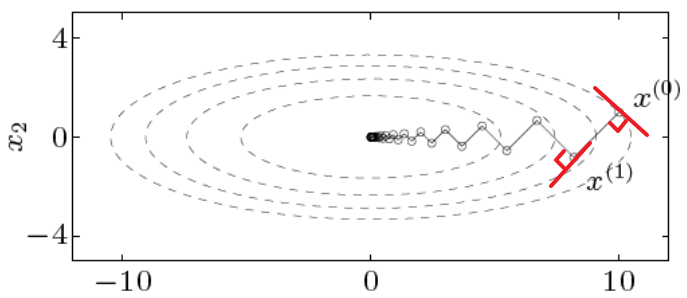
수렴 속도P의 설정
Gradient Descent는 현재 위치에서의 기울기,
즉 Local한 정보만을 활용하기 때문에
수렴 속도가 매우 느리다.		P의 설정에 따라 수렴 속도가 매우 달라짐
예시그림
\(f(\mathbf{x}) = \mathbf{x}_1^{2} + \gamma \mathbf{x}_2^2, \gamma > 0\)
\(\mathbf{x}^{(0)} = (\gamma, 1) \quad \text{& Exact Line Search}\)

\(\therefore \mathbf{x}_1^{(k)} = \gamma(\frac{\gamma - 1}{\gamma + 1})^k, \quad \mathbf{x}_2^{(k)} = (-\frac{\gamma - 1}{\gamma + 1})^k\)		alt text

$\qquad \Rightarrow$ Oscillate 발생

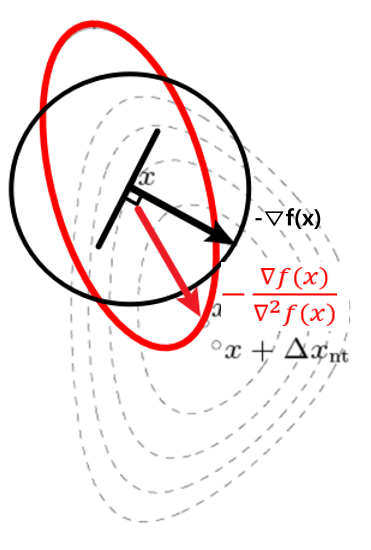
2) Newton’s Method

Interpretation그림
ⅰ Local Hessian Norm
$\quad$ Gradient Descent는 Local한 정보($\nabla f(\mathbf{x})$)만
$\quad$ 이용했기 때문에 문제가 발생하였다.

$\quad$ 즉, Global한 정보인 Hessian을 고려해야 하고
$\quad$ 이를 위해 방향마다 거리를 다르게 설정하는
$\quad$ Quadratic Norm을 활용할 수 있다.

\(\quad \therefore P = \nabla^2 f(\mathbf{x})\)
\(\quad \rightarrow \vartriangle \mathbf{x}_{sd} = - (\nabla^2 f(\mathbf{x}))^{-1}(\nabla f(\mathbf{x}))\)

ⅱ. Taylor Series
$\quad f(\mathbf{x})$를 $\mathbf{v}$만큼 움직였을 때의 함수를
$\quad$ Taylor Series의 2차항까지로 표현하면
$\quad$ 다음과 같다.
\(\quad f(\mathbf{x + v}) \approx f(\mathbf{x}) + \nabla f(\mathbf{x})\mathbf{v} + \frac{1}{2} \mathbf{v}^T \nabla^2 f(\mathbf{x})\mathbf{v}\)
$\quad$ 즉, 이 2차함수를 최소화하는 $\mathbf{v}$를 찾으면,
$\quad \mathbf{v} = \vartriangle \mathbf{x} = -\frac{\nabla f(\mathbf{x})}{\nabla^2 f(\mathbf{x})}$이다.		alt text

Newton’s Method는 위의 두가지 관점으로 해석할 수 있다.

Newton Decrement (Stopping Criterion)

Newton Decrement는 다음과 같이 정의된다.

\[\lambda(\mathbf{x}) = (\nabla f(\mathbf{x})^T \nabla^2f(\mathbf{x}^{-1}) \nabla f(\mathbf{x}))^{\frac{1}{2}} \\ \quad = (\vartriangle \mathbf{x}_{nt}^T \nabla^2 f(\mathbf{x}) \vartriangle \mathbf{x}_{nt})^\frac{1}{2}\]

이때, Newton Decrement는 다음과 같은 특징을 갖는다.
$f(\mathbf{x}) - \inf \limits_y \hat{f}(y) = \frac{1}{2} \lambda(\mathbf{x})^2$

즉 이 Newton Decrement가 0 에 가깝다면 최적점에 가까워졌다고 할 수 있고
따라서 이를 Stopping Criterion으로 사용할 수 있다.

Algorithm

1
2
3
4
5
6
7
8
9

not_stop = True
while not_stop:
  x = now
  x_nt = -Jacobian(f, x) / Hessian(f, x)
  decrement = x_nt.T @ Hessian(f, x) @ x_nt
  if (decrement / 2) < 0.01:
      not_stop = False
  step_size = Line_search(f, x, alpha, beta) 
  now = x + step_size * x_nt

특징

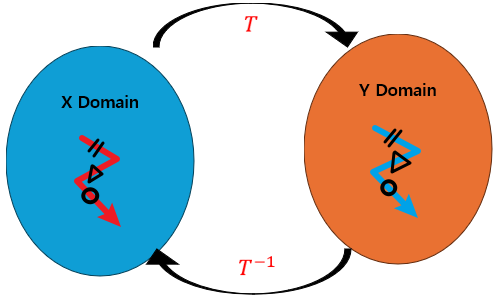
alt text

  • $\mathbf{x}$에 대한 함수를 $\mathbf{y} = T^{-1}\mathbf{x}$에 대한 함수로 Transform하더라도 Newton’s Method를 사용해 이동할 경우 Mapping관계가 그대로 유지된다.

2. Constrained Minimization

1) Equality Constrained Optimization

ProblemKKT Condition
\(\text{Minimize: } \quad f(\mathbf{x}) \\ \text{Subject to}: \quad A\mathbf{x} = \mathbf{b}\)

$A \in \mathbb{R}^{p \times n},$
$Rank(A) = p$
$\mathbf{x} \in \mathbb{R}^n,$
$f(\mathbf{x}) \text{는 Convex},$
$f(\mathbf{x}) \text{는 두번 미분 가능}$		\(\text{Primal Feasible: } \; \qquad A\mathbf{x}^* = \mathbf{b}\)
\(\text{Gradient of Lagrangian: } \quad \nabla f(\mathbf{x}^*) + A^T\nu^* = 0\)


※ Dual Residual: $r_d(\mathbf{X}, \nu) = \nabla f(\mathbf{x}) + A^T\nu$
※ Primal Residual: $r_p(\mathbf{x}, \nu) = A\mathbf{x} - \mathbf{b}$

※ Equality Constrained Quadratic Minimization일 경우 주의할 점이 필요하므로 이를 살펴보자.

ProblemKKT Matrix
\(\text{Minimize: } \quad \frac{1}{2} \mathbf{x}^{*T}P\mathbf{x}^* + q^T\mathbf{x}^* + r\)
\(\text{Subject to}: \; A\mathbf{x} = \mathbf{b}\)

—————————————————–
KKT Condition
\(P\mathbf{x}^* + q + A^T \nu = 0\)
\(A\mathbf{x}^* = \mathbf{b}\)
\(\qquad \Downarrow\)
\(\begin{bmatrix} P & A^T \\ A & 0 \end{bmatrix} \begin{bmatrix} \mathbf{x}^* \\ \mathbf{\nu}^* \end{bmatrix} = \begin{bmatrix} -q \\ \mathbf{b} \end{bmatrix}\)		\(K = \begin{bmatrix} P & A^T \\ A & 0 \end{bmatrix}\)
이때 문제를 풀기위해 KKT Matrix가
Non-Singular Matrix(역함수 존재)임을 가정하자.
$\Rightarrow \mathcal{N}(P) \cap \mathcal{N}(A) = \begin{Bmatrix} 0\end{Bmatrix}$
$\Rightarrow \mathbf{x}^TP\mathbf{x} + \Vert A\mathbf{x} \Vert^2 > 0 \quad \because$(P:정방행렬, A:비정방행렬)
$\Rightarrow P + A^TA \succ 0$
즉, 위 식이 성립하면 Unique한 Solution을 구할 수 있다.
(또 만약 $P \succ 0$일 경우에도 마찬가지이다.)

Eliminating Equality Constraint

KKT Condition으로도 문제를 풀 수는 있다.

하지만 앞서 배운 Unconstrained Optimization에서 사용하는 알고리즘들(Gradient Descent, Newton’s Method)를 사용하기 위해서는 Constraint를 없애줄 필요가 있다.

 $\mathbf{x} = \mathbf{x}_h + \mathbf{x}_p$
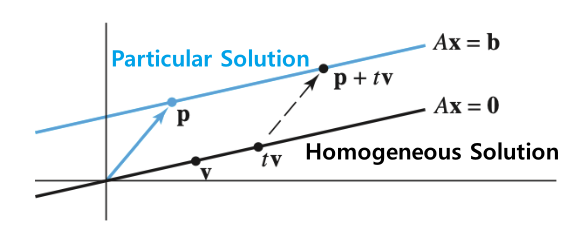
alt textNonhomogeneous System에서 배웠듯이 $A\mathbf{x} = \mathbf{b}$의 해는
Homogeneous Solution($A\mathbf{x} = 0$)과
Particular Solution($A\mathbf{x} = \mathbf{b}$)으로 나눌 수 있다.

이를 이용하여 Constraint가 존재하는 $\mathbf{x}$는 Constraint가 존재하지 않는 $\mathbf{z}$에 대한 식으로 바꿀 수 있다.

\(\qquad \begin{Bmatrix} \mathbf{x} \vert A \mathbf{x} = b \end{Bmatrix} \rightarrow \begin{Bmatrix} F\mathbf{z} + \hat{\mathbf{x}} \vert \mathbf{z} \in \mathbb{R}^{n-p} \end{Bmatrix} \\ \, \\F \in \mathbb{R}^{n \times (n-p)} \\ AF = 0, \quad (\mathcal{N}(A) = F)\\ A\mathbf{\hat{x}} = \mathbf{b} \qquad \qquad \qquad \quad\)\(\Rightarrow \qquad \underset{z}{\text{Minimize}} \quad f(F\mathbf{z} + \hat{x}) \qquad \qquad\)

즉 이 Unconstrained Minimization Problem의 해 $\mathbf{z}^*$를 구하고
$\mathbf{x}^* = F\mathbf{z}^* + \hat{\mathbf{x}}, \quad \nabla f(\mathbf{x}^*) + A^T \nu^* = 0$를 통해 원래의 해($\mathbf{x}^*, \nu^*$)를 알 수 있다.

Projected Gradient Method

alt text

다음 3개의 문제를 살펴보자.

Problem1Problem2Problem3
\(\underset{\mathbf{x}}{\text{Minimize}} \quad f(\mathbf{x}) \\ \text{Subject to} \quad A\mathbf{x} = \mathbf{b}\)\(\underset{z}{\text{Minimize}} \quad f(F\mathbf{z} + \hat{x})\)\(\underset{\mathbf{y}}{\text{Minimize}} \quad \Vert F\mathbf{y} - (-g) \Vert_2\)
—\(\mathbf{z}^* = F^T \cdot \nabla_\mathbf{x} f(F\mathbf{z} + \hat{\mathbf{x}}) \\ \vartriangle\mathbf{z} = -\mathbf{z}^*\)\(\mathbf{y}^* = -F^Tg\)
(if $F$ is Orthonormal basis)

우선 1번과 2번이 같은 문제임은 앞에서 증명하였다.

이때, 3번에서 $g= \nabla_\mathbf{z} f(F\mathbf{z} + \hat{\mathbf{x}})$라고 설정하면 2번문제의 Gradient Descent의 Step이 3번 문제의 Optimal인 점과 동일하다는 것을 알 수 있다.

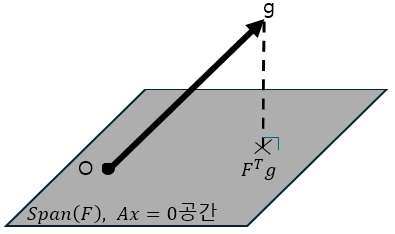
즉, $g = \nabla_\mathbf{x} f$를 $F$가 Span하는 공간 위로 Projection시킨 벡터가 해임을 알 수 있다.

이를 통해 알 수 있는 것은 Equality Constrained일 경우,
Unconstrained일때의 Gradient Descent의 Step은 Equality Constrained일 때
$A$의 Null Space(즉, Homogeneous해) 평면 위로
Projection되어 진행한다는 것이다.

Newton Step

Newton Step은 현재 위치에서 2차근사를 활용해 최솟값을 찾는 방식이다.
즉, 다음의 문제를 풀면된다.

ProblemKKT Condition
\(\underset{\mathbf{\nu}}{\text{Minimize:}}\; \hat{f}(\mathbf{x} + \mathbf{\nu}) = f(\mathbf{x}) + \nabla_\mathbf{x} f(\mathbf{x})^T \nu + \frac{1}{2} \nu^T \nabla^2_\mathbf{x} f(\mathbf{x}) \nu \\ \text{Subject to: }\quad A(\mathbf{x} + \nu) = \mathbf{b}\)ⅰ. Primal Feasible
\(A(\mathbf{x} + \nu) = \mathbf{b}\)
ⅳ. Gradient of Lagrangian
\(\nabla_\nu (\hat{f}(\mathbf{x} + \mathbf{\nu}) + A(\mathbf{x} + \nu) - \mathbf{b}) \\ = \nabla_\mathbf{x} f(\mathbf{x}) + \nabla^2_\mathbf{x}f(\mathbf{x}) \nu + A^Tw = 0\)

즉 다음의 Linear Equation의 Solution이다.

\[\begin{bmatrix} \nabla^2_\mathbf{x} f(\mathbf{x}) & A^T \\ A & 0\end{bmatrix} \begin{bmatrix} \nu \\ W \end{bmatrix} = \begin{bmatrix} -\nabla_\mathbf{x} f(\mathbf{x}) \\ 0 \end{bmatrix}\]

※ Newton Decrement: \(\lambda(\mathbf{x}) = (\vartriangle \mathbf{x}^T_{nt} \nabla^2 f(\mathbf{x}) \vartriangle \mathbf{x}_{nt})^\frac{1}{2} = (-\nabla f(\mathbf{x})^T \vartriangle \mathbf{x}_{nt})^\frac{1}{2}\)

2) Inequality Constrained Optimization

Irritation(Indicator) Function을 사용해서 Inequality로 바꾸자!

Original ProblemApproximated Problem
alt textalt text
\(\text{Minimize: } \quad f_0(\mathbf{x}) \\ \text{Subject to: } \quad f_i(\mathbf{x}) \leq 0 \\ \qquad\qquad \qquad A\mathbf{x} = \mathbf{b}\) $\qquad \qquad \Downarrow$
\(\text{Minimize: } \quad f_0(\mathbf{x}) + \sum \limits_{i=1}^m I_-(f_i(\mathbf{x})) \\ \text{Subject to: } \quad A\mathbf{x} = \mathbf{b}\)		\(\text{Minimize: } \quad f_0(\mathbf{x}) - \frac{1}{t} \sum \limits_{i=1}^m log(-f_i(\mathbf{x})) \\ \text{Subject to: } \quad A\mathbf{x} = \mathbf{b}\)
($t>0$는 Hyperparameter, 클수록 $I_-(x)$와 같아짐)
(Log barrier function: $\phi (\mathbf{x}) = - \sum \limits_{i=1}^m log(-f_i(\mathbf{x}))$)

$\nabla \phi(\mathbf{x}) = \sum \limits_{i=1}^m \frac{1}{-f_i(\mathbf{x})} \nabla f_i(\mathbf{x})$
$\nabla^2 \phi(\mathbf{x}) = \sum \limits_{i=1}^m \frac{1}{-f_i(\mathbf{x})^2} \nabla f_i(\mathbf{x}) \nabla f_i(\mathbf{x})^T + \sum \limits_{i=1}^m \frac{1}{-f_i(\mathbf{x})} \nabla^2 f_i(\mathbf{x})$

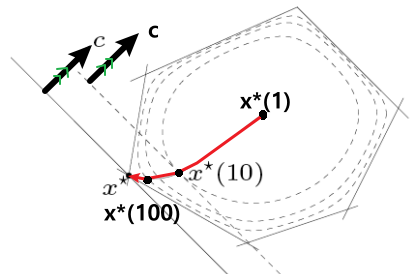
Central Path

Approximated Problem에서 t를 곱하고
이 식의 t에 따른 Solution의 경로$\mathbf{x}^*(t)$를
Central Path라고 한다.

$\text{Minimize:} \quad tf_0(\mathbf{x}) + \phi(\mathbf{x})$
$\text{subject to:}\quad A\mathbf{x} = \mathbf{b}$
alt text
ex) $f_0(\mathbf{x}) = c^T\mathbf{x}$
$\quad f_i(\mathbf{x}) = a_i^T \leq b_i$
\[\Downarrow\]

$\text{KKT Condition(ⅰ): } A\mathbf{x} = \mathbf{b}$
$\text{KKT Condition(ⅳ): } t \nabla f_0(\mathbf{x}) + \sum \limits_{i=1}^m \frac{1}{-f_i(\mathbf{x})} \nabla f_i(\mathbf{x}) + A^T \nu = 0$

\[\Downarrow\] \[f_0(\mathbf{x}^*(t) \geq p^* \geq g(\lambda^*(t), \nu^*(t))) \\ \qquad \qquad \qquad \qquad = L(\mathbf{x}^*(t), \lambda^*(t), \nu^*(t)) \\ \qquad \qquad \qquad \quad \qquad \qquad \qquad \quad = f_0(\mathbf{x}^*(t)) - \frac{m}{t} \quad (\text{m inequality #})\]

즉, 이 t의 크기를 통해 Optimal Value와의 오차를 조절할 수 있다.
따라서, Stopping Criterion을 정하고 t를 점차 키워가면서 Optimal Value를 구하는 알고리즘을 사용할 수 있다.

Algorithm

1
2
3
4
5
6
7
8
9
10
11
12

t = 10
mu = 10
tolerance = 1e-5

while True:
  initial_x = x
  step = minimize(t*f0(x) + phi, subject_to= (lambda x: Ax=b))
  
  x = last_optimal
  if m / t < tolerance:
      break
  t = mu*t

(t마다 Initial_x의 값을 계속 변화시키면서 Optimal을 찾는다.)
(전통적으로는 $\mu = 10 \sim 20$으로 설정한다.)
($\mu$가 너무 클 경우 Step을 계산하는 시간이 너무 오래걸린다. 즉, Trade off가 있다.)

alt text

\[(\text{Central Path Complexity, via }\mu)\]
Math, Convex Optimization
math
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.