3. Adversarial Search

Adversarial Search

Adversarial Search는 둘 이상의 프로그램이 서로 상충되는 목표를 가진 환경에서의 Search를 하는 문제들을 살펴본다.

이는 게임이론과도 관련이 있는데, 한 프로그램이 상대방 프로그램의 행동을 예측할 때
그 프로그램은 자신에게 가장 유리한 방향으로 행동할 것이고, 자신은 이러한 상황에서 가장 나은 방향으로 행동하고자 한다.

즉, 최악의 상황에서 최선의 선택을 하도록 Search한다.

1) Minimax Search

	Optimality	시간복잡도	공간복잡도
Minimax	O (상대방이 최선의 수를 두지 않아도 잘 작동)	$O(b^m)$	$O(bm)$

def Minimax_Search(start):
    value, nxt_state = max_Value(start)
    return nxt_state

def Max_Value(state):
    if state.is_terminal():
        return state.score(state.player)

    value, nxt_state = -1e9, None
    for child in expand(state):
        v = Min_Value(child)
        if value < v:
            value, nxt_state = v, child.state
    return value, nxt_state

def Min_Value(state):
    if state.is_terminal():
        return state.score(state.player)

    value, nxt_state = 1e9, None
    for child in expand(state):
        v = Max_Value(child)
        if value > v:
            value, nxt_state = v, child.state
    return value, nxt_state

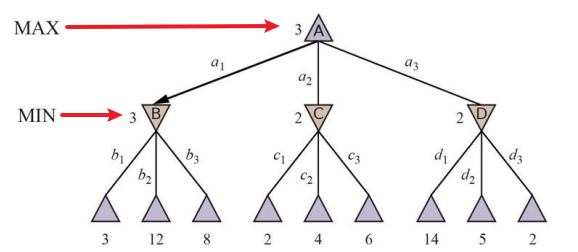
우선 내가 두어야 하는 상태를 root의 state로 두고 가능한 상태들의 Tree를 만든다.

이렇게 만들어진 Minimax Search Tree에는 Min, Max 노드가 존재한다.

• Min Node: Child중 utility가 가장 작은 것을 선택해야 하는 Node
• Max Node: Child중 Utility가 가장 큰 것을 선택해야 하는 Node

이제 다음을 주의하며 코드를 만들어보자

1. Root는 Max Node
   

   root는 현재 player가 “나”이기 때문에 가장 높은 효용을 갖는 상태를 선택하야한다.
   

2. Back Tracking
   

   각 Node는 Top-Down, 즉 확장시에 Value를 선택하는 것이 아닌,
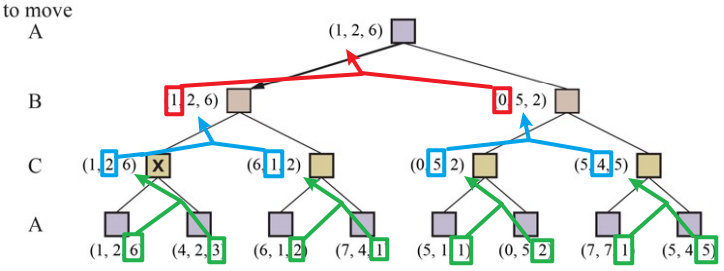
   Bottom-Up, 즉 수축시에 Child로부터 Value를 선택한다.

---

Multiplayer Games

각 Node는 자신의 child Node에서 자신의 위치의 효용이 가장 높은 것을 고르도록 구현한다.

2) Alpha-Beta Pruning

	Optimality	시간복잡도	공간복잡도
Minimax	O (상대방이 최선의 수를 두지 않아도 잘 작동)	$x \leq O(b^m)$	$O(bm)$

def Alpha_Beta_Search(start):
    alpha, beta = -1e9, 1e9
    value, nxt_state = max_Value(start, alpha, beta)
    return nxt_state

def Max_Value(state, alpha, beta):
    if state.is_terminal():
        return state.score(state.player)

    value, nxt_state = -1e9, None
    for child in expand(state):
        v = Min_Value(child, alpha, beta)     # <- Min_Value(child), 달라진 부분
        if value < v:
            value, nxt_state = v, child.state
            alpha = max(alpha, v)             # 달라진 부분(하계를 높임)
            if v >= beta:                     # 달라진 부분(상계를 넘어가면 pruning)
                return v, nxt_state           
    return value, nxt_state

def Min_Value(state):
    if state.is_terminal():
        return state.score(state.player)

    value, nxt_state = 1e9, None
    for child in expand(state):
        v = Max_Value(child, alpha, beta)
        if value > v:
            value, nxt_state = v, child.state
            beta = min(beta, v)               # 달라진 부분(상계를 낮춤)
            if v <= alpha:                    # 달라진 부분(하계를 내려가면 pruning)
                return v, nxt_state
    return value, nxt_state

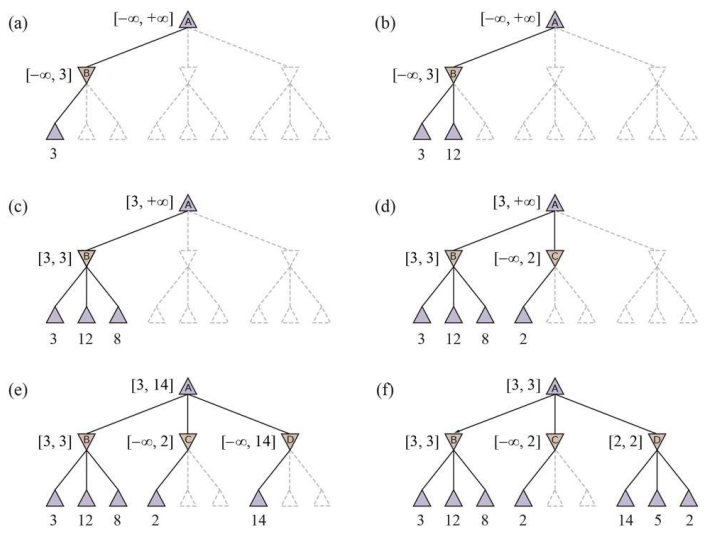
Minimax Search Tree에는 Search를 굳이 하지 않아도 되는 Node가 존재한다.

즉, 예를 들어 Min Node이면,
이전 Sibling의 Min값이 자신의 Min값보다 크다는 것이 확실할 때, 탐색을 멈추는 것이다.

이는 자신의 Parent Node인 Max Node에서 자신을 선택할 가능성이 없기 때문이다.

Alpha-Beta Pruning은 이러한 상/하계를 $\alpha, \beta$라는 변수로 관리하며 검색을 중단한다.

---

Heuristic Evaluation Function

Pruning을 하더라도 오목이나 바둑과 같이 수를 두는데 시간 제한이 있는 게임에서는 모든 Node를 탐색하기 힘들다.

이를 위해 Heuristic Evaluation Function인 “EVAL()”함수를 통해 이 예측치가 특정 값에 다다르면 cutoff하도록 설계할 수 있다.

Depth limit	Iterative Deepening	Quiescene Search	Singular Extension
깊이 제한	점진적 깊이제한	$\alpha, \beta$가 요동치지 않을 때까지 추가탐색	Horizon Effect를 막기 위함

3) Monte Carlo Tree Search

Heuristic Alpha-Beta Pruning은 Heuristic 알고리즘이 좋지 않다면 성능이 떨어진다는 단점이 있다.

이에 Monte Carlo는 Heuristic이 필요 없도록 만들어진 알고리즘이다.
방법은 매우 간단한데 그냥 게임이 끝날 때 까지 최대한 해보고 가장 가능성이 있는 Node를 선택한다.

def MTCS(state):
  tree = Node(state)
  while Time_remaining():
      leaf = SELECT(tree)     # Select 알고리즘
      child = EXPAND(leaf)
      result = SIMULATE(child)
      BACKPROPAGATE(result, child)
  return max(state.children, key=lambda x:x.total_visit)

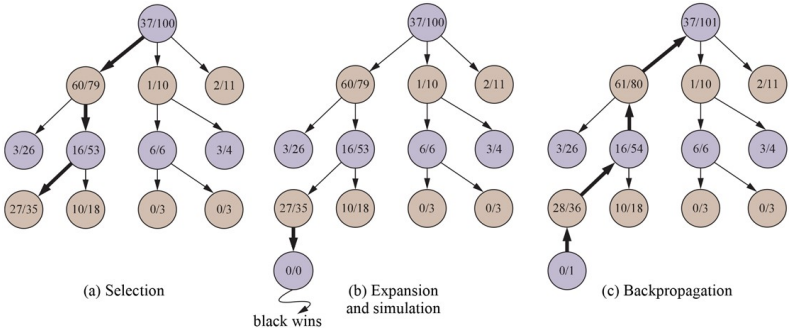
Phase
SELECT	Select Policy에 따라 Child Node들을 Leaf Node를 만날 때 까지 선택 선택정책은 다음 두 요소를 고려함 　ⅰ. 활용: 승률이 높은 Node들을 선택 　ⅱ. 탐험: 많이 방문해 보지 않은 Node들을 선택
EXPAND	선택된 Leaf Node에서 새로운 Child Node를 생성
SIMULATE (=ROLLOUT), (=PLAYOUT)	게임이 끝날 때까지 무작위로 플레이 하는 것 이때, PlayOut Policy를 만들면 성능이 좋아진다. (Simulation하면서 생성되는 State들은 기록하지 않는다.)
BACKPROPAGATE	SIMULATE결과를 Child Node 부터 Parent에 기록해 나감

---

SELECT Policy

대표적인 Select Policy로는 UCB정책이 있다.
이 UCB점수가 높은 Node들을 Select하는 방식이다.

\(UCB1(n) = \frac{U(n)}{N(n)} + C \sqrt{\frac{log(Parent(n))}{N(n)}} \\ \\ \frac{U(n)}{N(n)} \rightarrow Explitation \\ \sqrt{\frac{log(Parent(n))}{N(n)}} \rightarrow Exploration\) $N(x)$: x의 방문 횟수
$U(x)$: x의 승률
$Parent(x)$: x의 부모 Node
$n$: 현재 Node
C: 탐험과 활용의 균형을 위한 상수, 보통 $\sqrt{2}$를 사용