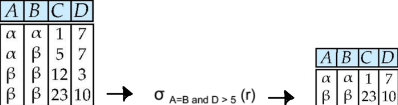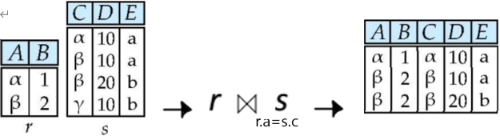2. Relational Algebra

Relational Operator

DataBase에 정보를 요청하는 언어를 Query Language 라고 한다. 이 Query Language에는 다음과 같이 추상적인 개념인 Pure Query Language가 존재한다.

현재 2, 3번째는 잘 사용되지 않고 있고, 따라서 여기서는 Relational algebra에 대해 알아보자.

먼저 Algebra는 다들 알고 있듯이, 수학적 구조들의 일반적인 성질을 연구하는 수학의 한 분야이다.
예를 들면 선형대수에서 행렬의 성질 즉, “행렬간 곱셈의 결과를 어떻게 도출할 것인가” 라던지 “행렬의 차원을 어떻게 정의할까” 라는 것을 생각해 볼 수 있을 것이다.

즉, Relational Algebra는 말 그대로 Table을 대상으로 한 대수학인데, 한개 혹은 두개의 Table(=Relation)을 입력으로 받았을 때 할 수 있는 계산(연산)들을 연구하는 것이라고 생각해 볼 수 있을 것이다.

이 Relational Algebra는 Functional Language라는 특징이 있다.

여기서 Functional Language와 Procedural Language를 헷갈릴 수 있는데 다음 예문을 보면 이해하기 쉬울 것이다.

• a = 1+2+3
• a = 1+add(2, 3)
• assign(a, add(1, 2, 3))

우선 결과부터 보면 첫번째와 두번째는 Procedural Language이고, 세번째는 Functional Language이다.

Procedural Language는 Procedural과 Function을 조합해서 사용하는 방법을 뜻하고, Functional Language는 모든 표현이 Function으로 이루어져 있는 것이다.

**그렇다고 Functional이라는 것이 Procedural하지 않다는 것이 아니다. 이 함수 안에는 당연히 Procedural한 코드가 작성되어 있을 것이기 때문이다.**

(참고: Procedural Language로 표현할 수 있는 수식은 전부 Functional Language로 표현이 가능하다.)

---

1. Basic Operator

다음은 다른 Operator로는 구현할 수 없는 Basic Operator이다.

---

먼저, 하나의 입력만 필요한 단항연산자를 살펴보자.

1) Select - 선택

• 기호: $\sigma_p(r)$
  • p: 선택할 N-Tuple의 조건을 입력하는 자리

  • r: Relation을 입력하는 자리

• 정의
  입력받은 Relation에서 조건을 맞는 N-Tuple들을 선택해 새로운 Relation을 만드는 연산
  • (Attribute: 주어진 Relation의 Attribute와 같음)

  • (Tuple: 조건에 맞는 Tuple만 선택)

• 예시
  

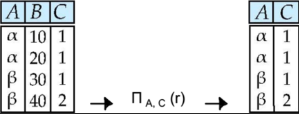
2) Project - 추출

• 기호: $\prod_{A_1, A_2, …, A_k}(r)$
  
  • A: 선택할 Attribute를 입력하는 자리

  • r: Relation을 입력하는 자리

• 정의
  입력받은 Relation에서 특정 Attribute를 뽑아내 새로운 Relation을 만드는 연산
  • (Attribue: 특정 Attribute만 선택)

  • (Tuple: 주어진 Relation Tuple과 같음)

• 예시
  

(여기서 Relational Algebra는 중복된 값이 없다는 것을 가정하기 때문에 따로 중복을 제거해줄 필요는 없다)

(반면에 SQL은 실제 DB를 대상으로 작동하므로 Project 연산 후에 반드시 중복을 제거해 주자.)

3) Rename - 재명명

• 기호: $\rho_{x_{(A_1, A2, … A_n)}}(E)$
  • x: 바꾸고 싶은 Relation의 이름
  • A: 바꾸고 싶은 Attribute의 이름 (순서 조심)

  • E: 이름을 바꿀 Relation을 입력하는 자리

• 정의
  입력받은 Relation에서 Relation Name 혹은 Attribute Name을 바꾸어 새로운 Relation을 만드는 연산 —

• 예시
  

  $\rho_i(instructor)$

---

다음으로는 연산시 두개의 입력이 필요한 이항연산자를 살펴보자

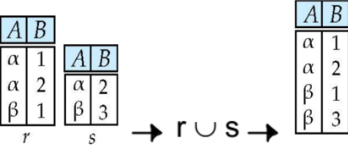
4) Union - 합

• 기호: $R \cup S$

  • r과 s는 모두 Relation

• 정의
  Relation Schema가 같은 두 Table에 대해 합집합을 수행하여 새로운 Relation을 만드는 연산
  • (Attribute: 주어진 Relation의 Attribute )
  • (Tuple: 두 Relation의 Tuple들의 합집합)

(조건: Relation의 Schema가 같아야 한다는 조건을 잊지말자)

---

• 예시
  

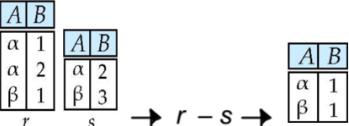
5) Set Difference - 차

• 기호: $R-S$

  • r과 s는 모두 Relation

• 정의
  Relation Schema가 같은 두 Table에 대해 차집합을 수행하여 새로운 Relation을 만드는 연산
  • (Attribute: 주어진 Relation의 Attribute )
  • (Tuple: 두 Relation의 Tuple들의 차집합)

(조건: 합집합과 마찬가지로 Relation의 Schema가 같아야 한다.)

---

• 예시
  

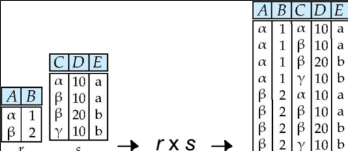
6) Cartesian Product - 곱

• 기호: $R \times S$

  • r과 s는 모두 Relation

• 정의
  입력받은 두 Relation의 Attribute를 합치고, 그 Instance는 두 Relation의 모든 조합을 표현하는 새로운 Relation을 만드는 연산
  • (Attribute: 두 Relation의 Attribute를 중복은 포함되게 합침)

  • (Tuple: Attribute의 모든 조합에 대한 값들을 표현)

• 예시
  

(예를 들어 만약 r의 Attribute에 C까지 포함 되어 있다고 가정해 보자, 이 때에는 r x s의 Attribute는 A, B, r.C, s.C, D, E가 될 것이다.)

---

Not Basic Operator

다음은 Basic Operator를 적당히 조합해서도 만들 수 있는 Operator 중에서 자주 사용되는 연산자를 알아보자.

---

1) InterSection

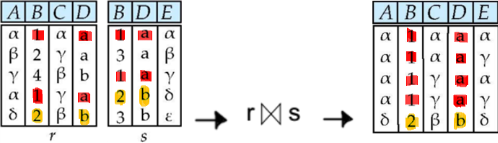
2) Natural Join

• 기호: $R \bowtie S$

  • r과 s는 모두 Relation

• 정의
  입력받은 두 Relation의 Attribute를 중복이 없도록 합치고, 그 Instance는 중복된 Attribute에서 Domain이 같은 경우만 표현하는 새로운 Relation을 만드는 연산
  • (Attribute: 두 Relation의 Attribute를 중복을 제거하고 합침)
  • (Tuple: 중복된 Attribute에서 Domain이 같은 경우의 값만 표현)

---

• 예시
  

3) Theta Join

• 기호: $R \bowtie_\theta S$
  • r과 s는 모두 Relation

  • Theta: 선택할 조건

• 정의
  입력받은 두 Relation을 Catesian Product를 통해 합친 후에 주어진 조건에 해당하는 Tuple만 표현하는 새로운 Relation을 만드는 연산
  • (Attribute: 두 Relation의 Attribute를 중복을 포함하여 합침)
  • (Tuple: Catesian Product후에 주어진 조건에 해당하는 것만 선택)
• $R \bowtie_\theta S = \sigma _\theta(R \times S)$

---

• 예시