7. Normalization
Abstract
앞의 E-R Model과 EE-R Model을 통해 DataBase를 표현하는 방법에 대해서 배웠다면,
이제는 DataBase를 어떻게 구성해야 하는지 알아보도록 하자.
DataBase를 구성하는데 있어 가장 중요한 점은 추후 Insertion이나 Modification등을 사용하여 같이 Relation을 사용하는데 있어 문제가 발생해서는 안된다는 것이다.
이때 발생 가능한 문제는 다음과 같다,
발생 가능한 문제점
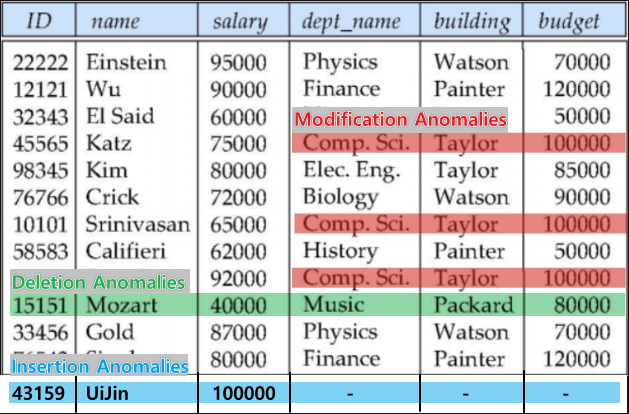
1. Insertion Anomalies(파란색 마크)
문제상황
- 어떤 학교의 Employee를 나타내는 Table에 아직 부서(department)가 정해지지 않은 Employee를 추가하고 싶다.해결방안
- 부서를NULL로표시
- 부서를임시정보로 표시문제점
- 저장공간의 낭비가 발생한다.2. Deletion Anomalies(초록색 마크)
문제상황
- 이 회사에 부서(department)를 저장하는 별도의 Table이 없다고 하자.
- Mozart라는 Employee를 삭제하고 싶다.해결방안
- 해당 Tuple Delete결과
- 의도치 않은 정보의 손실이 발생한다.
(더이상 Music이라는 부서는 존재하지 않게됨)3. Modification Anomalies(빨간색 마크)
문제상황
- 이 회사에 Computer Science학과가 다른 건물로 옮겨졌다.해결방안
- Computer Science를 갖고있는 모든 Tuple을 수정한다.결과
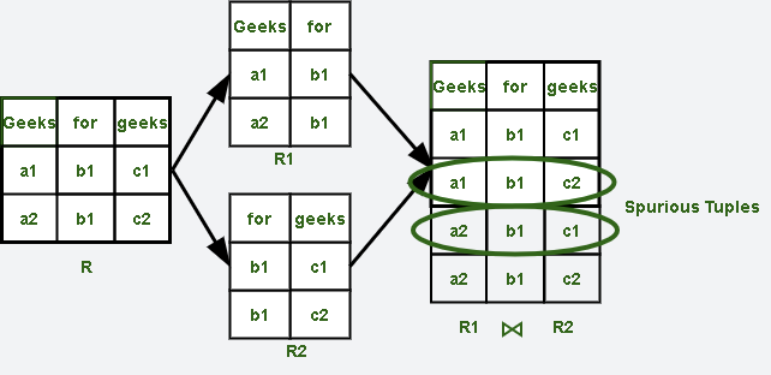
- Modification에 대한 Time Complexity가 증가한다.4. Join Anomalies(Spurious Tuple)
위의 문제들 이외에도 위와 같은 경우가 있을 수 있다.
어떤 Table $R$ 나누어 $R1$, $R2$ Table을 만들었을 때, 이 두 Table을 Join하여 $R$을 만들 경우, 원래 $R$에는 존재하지 않던 Tuple이 발생하게 된다.
즉, DB를 제대로 Design하지 않고 Table을 생성할 경우 위와 같은 문제들이 발생할 수 있고,
이는 주로 데이터가 중복저장되어 저장공간이 낭비되거나 어플리케이션의 실행 시간을 늘리는 문제를 야기한다.
해결책
위 문제들의 해결책은 다음과 같다
- Attribute간의 종속관계를 분석해 여러 Relation으로 분리해야 한다.
- 하나의 Table은 하나의 Relation(Entity)에 대한 정보만을 나타내야 한다.
- 기본키, 외래키 조합을 통해 무손실 조인을 만족하도록 설계해야 한다.
- 무손실 Join: 어떤 Table $R$을 $R1$, $R2$로 나누었을 때, $R1$ $JOIN$ $R2$를 하면 $R$을 만들 수 있는 경우
- `NULL`값이 많은 Attribute의 경우 별도의 Relation으로 분리한다.
NULL의 단점1: 저장공간 낭비NULL의 단점2: Join의 결과를 예측하기 힘듦NULL의 단점3: Attribute의 의미를 이해하기 힘듦NULL의 의미
FD Normalization
이제 위에서 간단하게 알아보았던 문제들을 정의하고 해결하는 방법을 알아보도록 하자.
우선 위에서 보았던 문제상황은 Functional Dependency를 만족하지 않았기 때문에 발생한다.
또한 이에 대한 해결방법, 즉 Functional Dependency를 얼마나 만족하는지는 Normal Form을 통해 표현할 수 있다.
1. Functional Dependency
Funtional Dependency는 좋은 Data Base Schema를 만들기 위해 사용자가 정한 규칙으로, 현재 존재하는 Tuple과 앞으로 입력될 모든 Data에 대해 적용된다.
1) 정의
α ⊆ $R$, β ⊆ $R$인 α ,β 와 두 Tuple $t1, t2$에 대해
$t1[\alpha]=t2[\alpha]$이면 $t1[\beta]=t2[\beta]$ 이 성립하는 경우 Functional Dependency가 성립한다고 한다.
- 표기: α → β
- 즉, α 의 값이 β 의 값을 유일하게 결정하는 관계
(어떤 Attribute Set이 다른 Attribute Set을 결정(구분)하는 관계)(참고: α → β이고, α ⊇ β 일 때, α → β는 Trivial한 Functional Dependency를 갖는다고 한다.)
2) 종류
α → β 가 성립한다고 하자.
즉 α가 β의 Key역할을 하고 있다.Full Functional Dependency
$\alpha’$ ⊂ $\alpha$에 대하여 $\alpha’$ ⊂ $\beta$인 $\alpha’$이 존재하지 않을 때 Full Functional Dependency를 만족한다고 한다.
즉, Table의 Attribute β에 대해 어떠한 Key의 Subset도 β의 Key가 될 수 없을 때
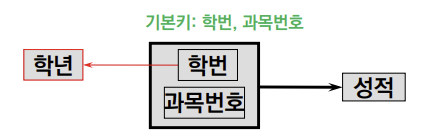
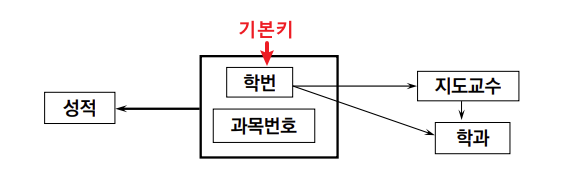
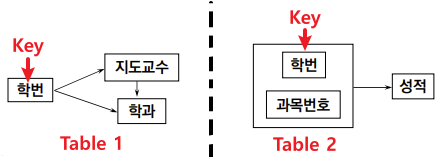
ex. 학년은 {학번}과 완전 함수 종속 관계이다.
ex. 성적은 {학번, 과목번호}와 완전 함수 종속 관계이다.Partial Functional Dependency
$\alpha’$ ⊂ $\alpha$에 대하여 $\alpha’$ ⊂ $\beta$인 $\alpha’$이 존재할 때 Partial Functional Dependency를 만족한다고 한다.
즉, Table의 Attribute β에 대해 Key의 Subset또한 β의 Key가 될 수 있을 때
ex. 학년은 {학번, 과목번호}와 부분 함수 종속 관계이다.
Transitivity Functional Dependency
α → β이고 β → γ일 때, γ는 α에 Transitivity Dependency를 갖는다고 한다.
즉, 직접적인 Dependency는 없으나 다른 Attribute를 거쳐 결정되는 관계에 있는 상태를 의미한다.
3) Closure(폐포)
FD의 Closure
- 정의
- Functional Dependency를 표현한 집합 F에 대해 이 F를 통해 유도 가능한 모든 Functional Dependency의 집합
- 표기
- $F^+$
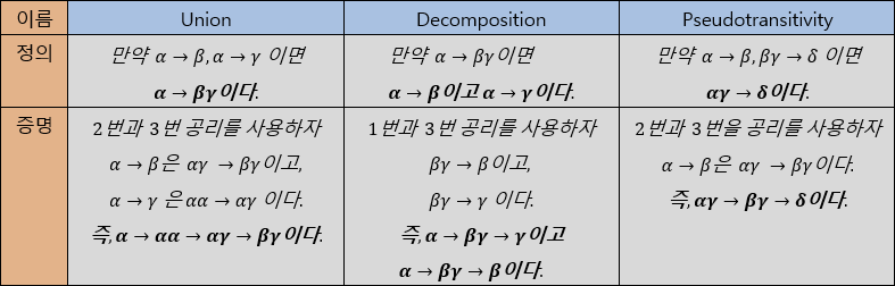
1. Armstrong’s Axiom(공리)
2. Additional Rules
Attribute의 Closure
- 정의
- Attribute Set을 표현하는 $A$에 대하여 이 A가 Functional Dependency를 통해 결정 가능한 모든 Attribute Set의 집합
- 표기
- $A^+$
구하는 방법
- $A$가 Functional Dependency로 결정 가능한 Attribute Set $B$를 구한다.
- $B$가 Functional Dependency로 결정 가능한 Attribute Set들을 구해 $A^+$를 구한다.
- $A^+$를 사용해 1번부터 $A^+$가 변하지 않을 때까지 반복한다.
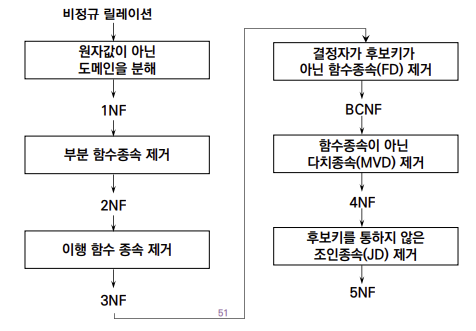
2. Normal Form
위에서 보앗듯 Anomalies를 줄이기 위해서는 반드시 한 Table에 존재하는 Functional Dependency를 줄여야 한다.
하지만 이 Functional Dependency를 마냥 줄일 수 만은 없는데
다음 글을 읽으며 이 이유에 대해 생각해보자.
#정의
여기서 우리의 최종적인 목표는 Third Normal Form을 만족하거나 BCNF를 만족하는 데이타베이스를 설계하는 것이다.
Normal Form이란 정해진 특정 제약 조건을 만족하는 형태의 Relation이다.
이때, 이 조건은 Data의 Redendency를 줄이기 위한 조건으로, Functional Dependency의 관점에서 정의된다.
또한 이 조건은 1NF에서 BCNF로 갈수록 점점 추가된다.
이 조건에 의해서 Relation은 Decompose되는데 이때 유의할 점은 다음과 같다.
- Lossless-join Decomposition
- Decompose시 Loss가 발생해서는 안된다. (모든 Normal Form이 만족)
- Lossless-join Decomposition
- Dependency Preserving
- Decompose결과 Relation과 Functional Depedency가 각각 ($R1, R2$), ($F1, F2$)로 나누어졌을 때,
$F1$과 $F2$를 위해서 $R1$과 $R2$의 Join연산이 필요하지 않아야 한다.
- Dependency Preserving
Dependency Preserving예시
$R=(A, B, C)$
$F=(A\rarr B, B\rarr C)$
- if, $R1=(A, B), R2=(B, C)$
- Dependency Preserving을 만족한다.
- if, $R1=(A, B), R2=(A, C)$
- Dependency Preserving을 만족하지 않는다.
1) First Normal Form
1. 정의
**모든 Attribute의 domain은 atomic해야 한다.**
atomic은 나눌 수 없다는 뜻이다.
즉, Data Base를 사용할 때, 해당 Attribute를 Parsing해서 사용할 경우에 대해서는 배제하고 설계해야한다.우리는 이 조건으로 인해 DB의 설계 측면과 사용 측면의 역할을 나눌 수 있게 된다.
2. FD와의 관계
**"모든 Relation은 Functional Dependancy가 존재해야 한다."**
만약 Multivalue Attribute가 존재한다고 하면 이 값들을 결정하기 위해, Functional Dependency가 사라지게 된다.
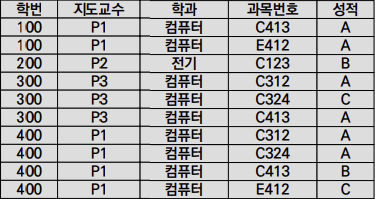
3. 문제점
- Insertion Anomalies
- 500번 학생의 지도교수가 P4라는 사실을 넣을 때,
Key조건에 의해{학번, 교과목}이라는 필요없는 정보도 넣어야 함
- Deletion Anomalies
- 200번 학생의 C123과목의 수강취소를 할 때,
200번 학생의 지도교수에 대한 정보도 사라짐
- Modification Anomalies
- 400번 학생의 지도교수를 변경할 때,
4개의 Tuple을 모두 변경해야 함
2) Second Normal Form
1. 정의
- Relation이 First Normal Form을 만족한다.
- **모든 Attribute들이 Key에 대해서 완전 함수 종속(Full Functional Dependent)이어야 한다.**
즉, Key의 어떠한 Subset도 Table의 어떠한 Attribute를 결정할 수 없어야 한다.
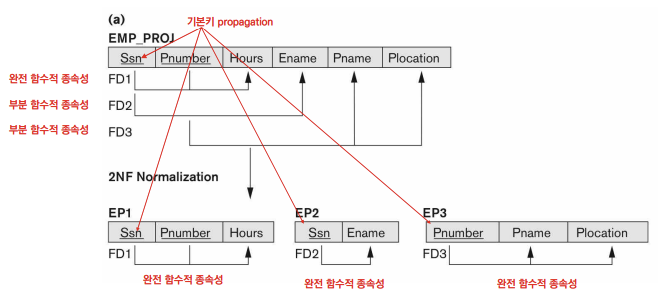
2. First Normal Form → Second Normal Form
3. 문제점
- Insertion Anomalies
- 지도교수가 P4가 속한 학과가 기계과라는 사실을 넣을 때,
Key조건에 의해{학번}이라는 필요없는 정보도 넣어야 함
- Deletion Anomalies
- 200번 학생이 졸업해 Tuple을 삭제하게 되면,
지도교수 P2가 전기과에 속한다는 정보도 사라짐
- Modification Anomalies
- 지도교수 P1의 소속학과를 변경한다면,
2개의 Tuple을 모두 변경해야 함
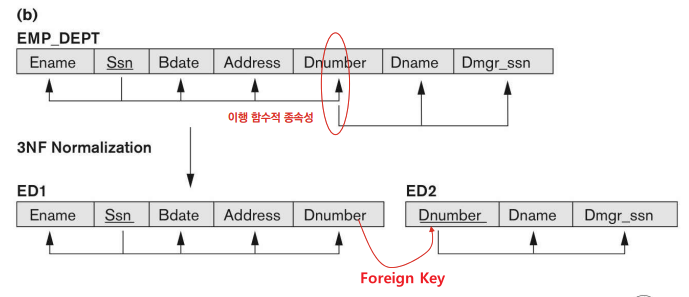
3) Third Normal Form
1. 정의
- Relation이 Second Normal Form을 만족한다.
- **Key로부터 Transitivity Functional Dependency가 존재하는 Attribute가 없는 Relation이어야 한다.**
즉, Key가 결정하는 Attribute가 다른 Attribute를 결정하는 일이 없어야 한다.
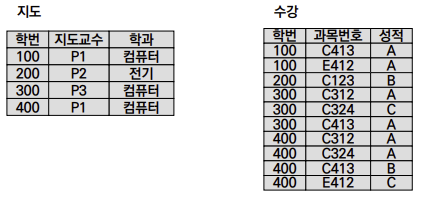
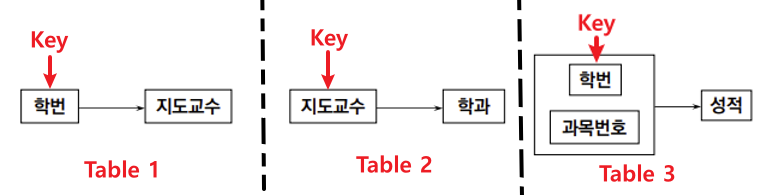
2. Second Normal Form → Thrid Normal Form
3. 문제점
위와 같이 나뉜 경우 발생하는 문제는 없다.
하지만 아래와 같은 경우를 살펴보자.
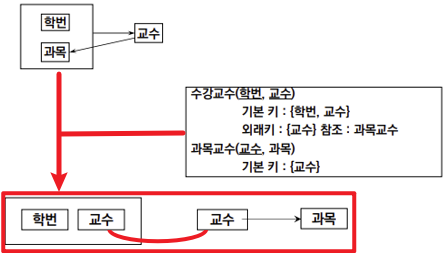
- (1) 복수의 후보키를 가짐
{학번, 과목},{교수}의 2개의 Candidate Key가 있음- (2) 후보키가 Multi Attribute로 구성됨
{학번, 과목}는 2개의 Attribute로 구성됨- (3) 이 후보키들이 서로를 가리킴
{학번, 과목}→{교수},
{교수}→{과목}이 경우 Second Normal Form도 만족하고 Transitivity Functional Dependency가 존재하지 않기 때문에
Third Normal Form의 형태에 포함된다.
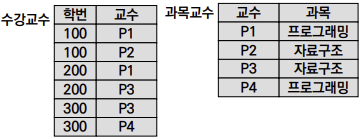
- Insertion Anomalies
- 교수 P5가 자료구조를 담당한다는 사실은,
Key조건에 의해 수강학생의{학번}이라는 필요없는 정보도 넣어야 함
- Deletion Anomalies
- 100번 학생이 자료구조를 수강취소해 Tuple을 삭제하게 되면,
지도교수 P2가 자료구조의 담당 교수라는 사실도 삭제됨
- Modification Anomalies
- 지도교수 P1의 담당 과목이 자료구조로 변경되면,
2개의 Tuple을 모두 변경해야 함즉, Third Normal Form의 경우 특정한 경우에만 문제가 발생한다.
.png)
.png)
4) Boyce-Codd Normal Form
1. 정의
- Relation이 Third Normal Form을 만족한다.
- **Key를 제외한 Attribute에 대해서는 Functional Dependency가 존재해서는 안된다.**
즉, Key를 제외한 Attribute는 다른 Attribute를 결정해서는 안된다.
2. Third Normal Form → BCNF
Functional Dependency에서 Determinant역할을 하지만 Candidate Key가 아닌 것을 분리한다.
3. 단점
- Dependency Preserving이 보장되지 않는다.
- 기존의
{학번, 과목}이{교수}를 결정한다는 Functional Dependecy에 대한 정보는
두 Table을 Join하기 전까지는 확인이 불가능하다.따라서 Functional Depedency를 검사할 일이 많다거나 동작 시간을 단축시키고 싶을 경우 BCNF를 사용하지 않을 수 도 있다.
즉, 3NF는 BCNF보다는 중복을 조금 더 허용 하더라도 Dependency Preserving을 보장하는 형태라고 할 수 있다.
5) Normalization Example
Case1
- Key
Primary Key: ${A, B} \rarr {A, B, C, D, E, F, G, H}$
- To 2NF
- $R_1={\underline{A, B}, C}$
- $R_2={\underline{A}, D, E}$
- $R_3={\underline{B}, F, G, H}$ , (4번 FD는 3번 FD에 의해 결정되므로 3번 FD에 통합)
- To 3NF
- $R_1={\underline{A, B}, C}$
- $R_2={\underline{A}, D, E}$
- $R_3={\underline{B}, F, G}$
- $R_4={\underline{F}, H}$
Case2
- Key
Primary Key: ${A, B} \rarr {A, B, C, D, E, F, G, H, I, J}$
- To 2NF
- $R_1={\underline{A, B}, C}$
- $R_2={\underline{A}, D, E, I, J}$, (5번 FD는 1번 FD에 의해 결정되므로 1번 FD에 통합)
- $R_3={\underline{B}, F, G, H}$, (4번 FD는 3번 FD에 의해 결정되므로 3번 FD에 통합)
- To 3NF
- $R_1={\underline{A, B}, C}$
- $R_2={\underline{A}, D, E}$
- $R_3={\underline{D}, I, J}$
- $R_4={\underline{B}, F}$
- $R_5={\underline{F}, G, H}$
Case3
- Key
Primary Key: ${id} \rarr {id, Country_name, Lot#, Area, Price, Tax_rate}$
Candidate Key: ${Country_name, Lot#} \rarr {id, Country_name, Lot#, Area, Price, Tax_rate}$
- To 2NF
- $R_1={\underline{id}, Country_name, Lot#, Area, Price}$
- $R_2={\underline{Country_name}, Tax_rate}$
- To 3NF
- $R_1={\underline{id}, Country_name, Lot#, Area}$
- $R_2={\underline{Country_name}, Tax_rate}$
- $R_3={\underline{Area}, Price}$
Case4
- Key
Primary Key: ${Title, Author} \rarr {Title, Author, Type, Price, Author_affil, Publisher}$
- To 2NF
- $R_0={\underline{Title}, \underline{Author}}$ (R1과 R2의 Join을 위해 Relation을 새로 만들었다.)
- $R_1={\underline{Title}, Type, Publisher, Price}$
- $R_2={\underline{Author}, Author_affil}$
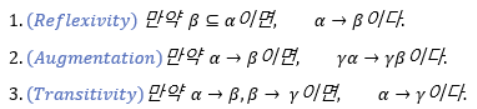
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)