4. 3D Computer Vision

3D Computer Vision

2D Computer Vision의 표현 방법은 하나밖에 존재하지 않았다.
하지만, 3D Computer Vision의 표현 방법은 매우 다양하다.

따라서 이를 먼저 알아보고 각 표현 방법들을 다루는 방법들을 알아보자.

1. BackGround

1) Coordinate

좌표계

월드 좌표계	카메라 좌표계	픽셀 좌표계
물체의 위치를 표현할 때 기준으로 삼는 좌표계 (임의로 설정 가능)	1. 카메라의 초점을 원점으로한 좌표계 2. 방향 　ⅰ. 원점: 카메라의 초점 　ⅱ. x축: 카메라의 오른쪽 　ⅲ. y축: 카메라의 아래쪽 　ⅳ. z축: 카메라의 정면	1. 투영된 이미지의 좌표계 2. 방향 　ⅰ. 원점: 이미지의 왼쪽 상단 　ⅱ. x축: 카메라의 오른쪽 　ⅱ. y축: 카메라의 아래쪽

※ 정규 좌표계: 카메라 내부 파라미터의 영향이 없을 경우 투영되는 공간에 대한 좌표계

---

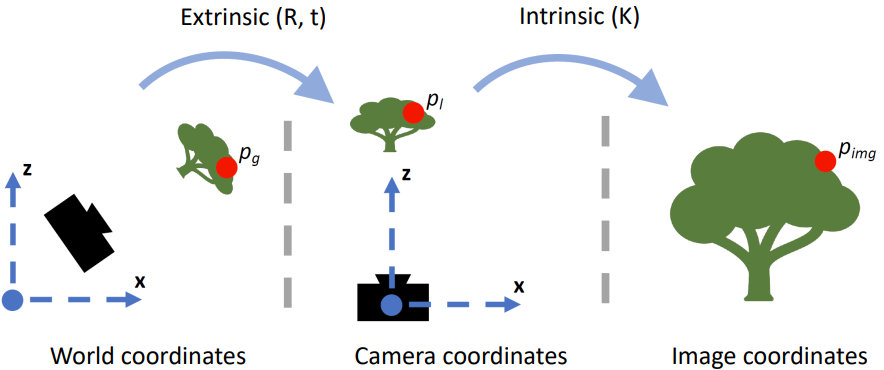
파라미터

	외부 파라미터 행렬	내부 파라미터 행렬
변환	월드좌표계 $\rightarrow$ 카메라 좌표계	카메라 좌표 $\rightarrow$ 카메라 영상의 픽셀값 (카메라 내부의 기계적인 셋팅)
요소	1. 회전이동 2. 평행이동	1. 초점거리: 렌즈의 중심과 CCD/CMOS와의 거리 2. 주점: 렌즈의 중심에서 이미지 센서에 수직으로 $\qquad \quad$ 내린 점의 영상픽셀좌표 3. 비대칭 계수: 이미지 센서의 y축이 기울어진 정도 4. 렌즈왜곡 5. 영상의 중심값 6. 이미지 센서의 Aspect Ratio 7. 이미지센서의 Skew Factor

(렌즈왜곡 모델: 방사형 렌즈왜곡, 접선형 렌즈왜곡)

2) Representation

Depth Map	Voxel Grid	PointCloud
카메라와 픽셀사이의 거리	3D Grid로 표현	Point들의 “집합”으로 표현 (Volume: X, Location: O)
(+) 2D 이미지 활용 가능	(+) 개념적으로 이해하기 쉽다	(+) 적은 수의 점으로 구조 표현 가능
(-) 3D Task를 수행하기 어려움	(-) detail한 표현을 위해서는 $\;\;\;$ 메모리가 많이 필요하다. $\;\;\;$(3D Kernel $\rightarrow$ 3D CNN 사용)	(-) Surface표현 불가능 (-) 새로운 Loss가 있어야 함 $\;\;\;$ (점들의 “집합”이기 때문)

Mesh	Implicit Surface
“Vertics”와 “Face”로 이루어진 삼각형들의 “집합” ● Vertics: 삼각형의 모서리 ● Face: 삼각형의 면	3D Shape를 함수로 표현하는 방법
(+) Computer Graphic에서 주로 사용하는 방법 (+) Detail한 표현이 필요한 부분은 Face를 $\quad$ 더 사용하므로써 Adaptive한 표현 가능 (+) UV Map같은 것을 활용해 Color, Texture 같은 $\quad$ 추가적인 정보도 표현 가능	(+) 세부적인 표현이 가능
(-) Nerual Nets에서는 처리하기 쉽지 않음 $\quad$ (Graph Convolution)	(-) 개념이해가 필요

---

2. Depth Estimation

1) Stereo Matching

2) Monocular Depth Estimation

방법	문제점
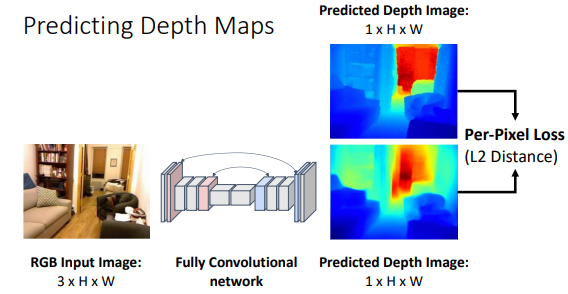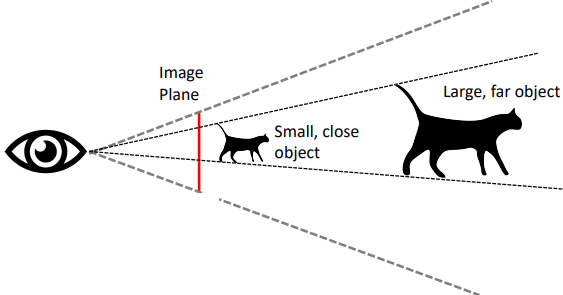Segmentation모델과 비슷하게 Pixel별로 Depth를 Regression하면 된다. (ex. UNet)	Scale/Depth Ambiguity 작고 가까운 물체와 크고 멀리있는 물체를 구분할 수 없다. 때문에 하나의 이미지로는 Relative Depth만 구할 수 있다.

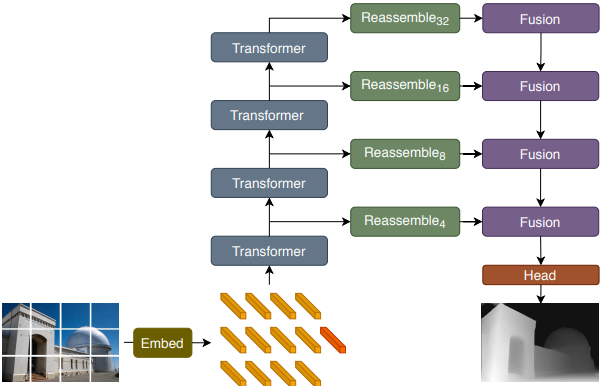
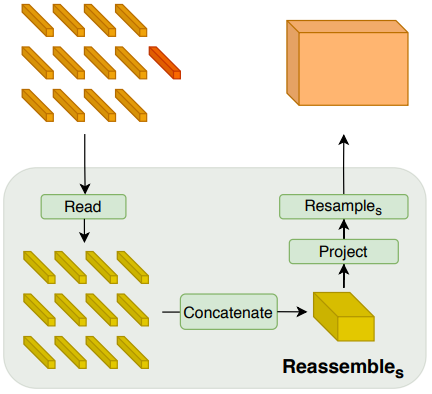
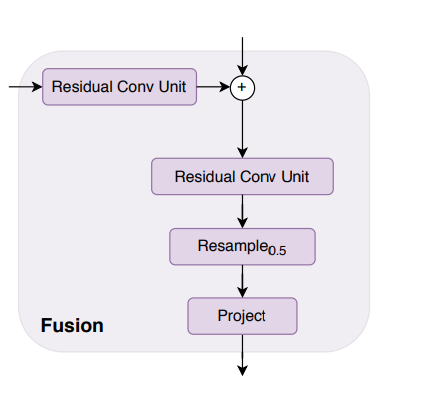
Paper1: DPT

Vision Transformers for Dense Prediction이라는 논문에서는 다음과 같은 방법을 제안한다.

Architecture	Abstract
	기존의 Dense Prediction에서 좋은 성능을 내는 모델들은 다음 두가지의 특징을 갖는다. ● Encoder-Decoder 구조 ● CNN Backbone 이때, CNN Backbone의 경우 DownSampling을 통해 다양한 Scale의 Feature를 추출한다. 이때, 기존의 정보를 잃을 수 있지만 Segmentation에서는 이를 어느 정도 해결할 수 있었다. 하지만 높은 해상도와 Detail이 요구되는 Dense Prediction에서는 이 DownSampling과정은 적합하지 않다. $\Rightarrow$즉, DownSampling이 일어나지 않는 ViT를 사용해보자

이 Architecture는 Detection의 FPN과 비슷하게 동작하게 된다.

Reassemble Layer	Fusion Layer
ⅰ. Read $\quad$: $N_p+1$개의 토큰을 $N_p$개의 토큰으로 변환 ⅱ. Concatenate $\quad$ :$\frac{H}{p} \times \frac{W}{p} \times D$의 하나의 Block으로 변환 ⅲ. Resample $\quad$: Output Size와 맞추기 위한 Upsampling과정	RefineNet기반 Feature Fusion Block UNet구조와 비슷하게 Feature Map을 결합하고 점진적으로 2배씩 Upsampling

---

Paper2: Depth Anything

---

3. Point Cloud

1) Classification

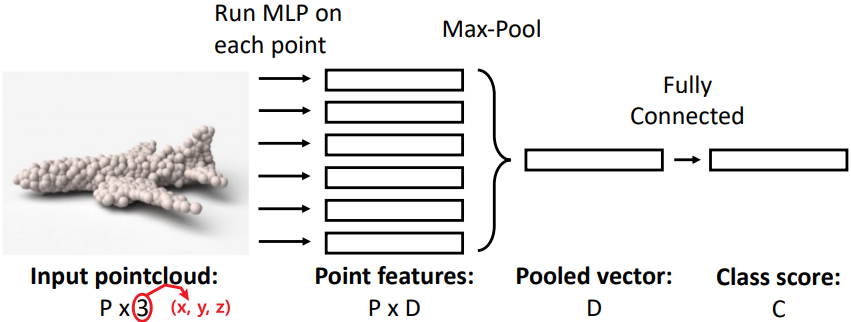
Paper1: PointNet

Architecture	Abstract
	Point Cloud같은 데이터는 다음의 단점이 존재한다. ● Irregular ● Unordered 이 때문에 학습이 쉽지 않고, Voxel로 바꿀 경우 데이터의 부피가 매우 커진다. $\Rightarrow$ Raw Point Cloud를 Input으로 하는 모델 제안

2) 3D Reconstruction

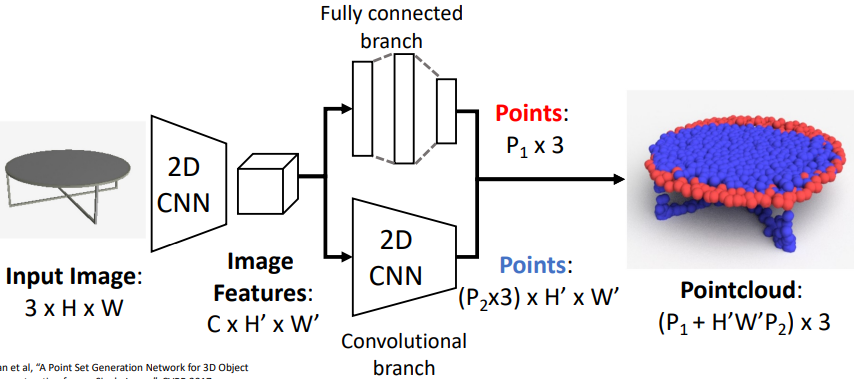
Paper1: Point Set Generation Network(PSGN)

Architecture	Abstract
	하나의 2D Image를 통해 3D Point Cloud를 생성하는 모델로 기존의 Volumetric Grid나 Collection of Image방식은 다음의 단점이 존재한다. ● 기하학적 변환시 3D형태의 불변성 모호 ● 이외에도 다양한 문제 존재 $\Rightarrow$ Point Cloud를 생성하는 방식의 모델 제안

이때, 생성된 Point Cloud는 순서가 존재하지 않는 “집합”이므로 집합간의 차이를 비교할 수 있는 새로운 방식의 Loss가 필요하다.

Chamfer Distance

\[d_{CD}(S1, S2) = \sum \limits_{x \in S_1} \min \limits_{y \in S_2} \Vert x-y \Vert_2^2 + \sum \limits_{y \in S_2} \min \limits_{y \in S_1} \Vert x-y \Vert_2^2\]

• $\sum \limits_{x \in S_1} \min \limits_{y \in S_2} \Vert x-y \Vert_2^2$
  

  
  

  각 예측값$x$에 대해, 정답값$y \in S_2$중 Nearest Neighbor와의 거리$d_i$를 구하고 $\sum \limits_i d_i$

• $\sum \limits_{y \in S_2} \min \limits_{y \in S_1} \Vert x-y \Vert_2^2$
  

  
  

  각 정답값$y$에 대해, 예측값$x \in S_1$중 Nearest Neighbor와의 거리$d_i$를 구하고 $\sum \limits_i d_i$

---

4. Predicting Meshes

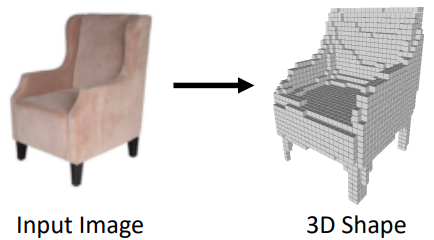
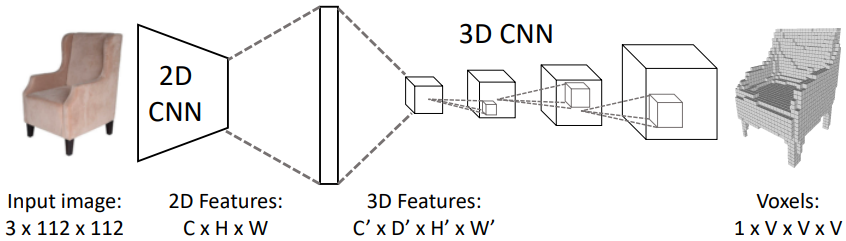
1) 3D Reconstruction

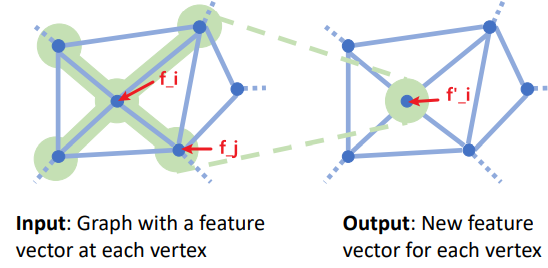
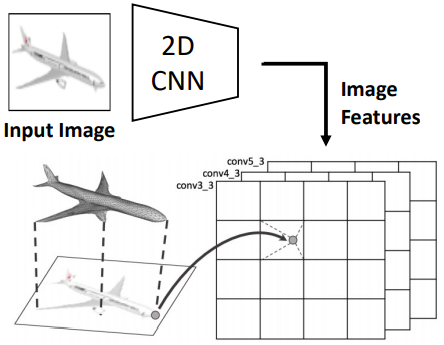
Paper1: Pixel2Mesh

Architecture
Abstract	기존의 방식은 Multi-View Geometry(MVG)를 기반으로 연구되었다. 하지만 이 방식은 다음과 같은 문제를 갖는다. ● MVG가 제공할 수 있는 범위에 한계가 존재 $\;\;$(보이지 않는 곳 표현 불가) ● Reconstruction하고자 하는 객체의 외관에 의해 한계 존재 $\;\;$(“투명”하거나 “빛을 반사”하는 물체, “Textureless” 물체는 Reconstruction불가) 이를 해결하기 위해 Mesh를 직접 합성하는 대신, 타원체를 점진적으로 대상 3D Mesh로 변형하는 방법을 제안 (Corse-To-Fine 전략)

\[\Updownarrow\]

Graph Convolution	Vertex-Aligned Feature
\(f_i' = W_0f_i + \sum \limits_{j \in N(i)} W_1 f_j\) Mesh는 삼각형의 Vertex로 이루어져 있기 때문에, 하나의 Vertex의 움직임은 인접한 Vertex에 영향을 주어야 한다. 이러한 특징을 반영하여 새롭게 구성한 Layer가 Graph Convolution Layer이고 위의 Architecture는 이 Stack of Graph Convolution Layer이다.	ⅰ. 2D 이미지에서 Feature Map 추출 ⅱ. 추출된 Feature Map을 3D 모델에 매칭 (3D모델을 2D이미지 평면에 투영 후 매칭) ⅲ. 각 정점에는 이제 해당 위치와 대응되는 $\quad$ Image의 Feature를 갖게 됨

\[\Updownarrow\]

Loss Function

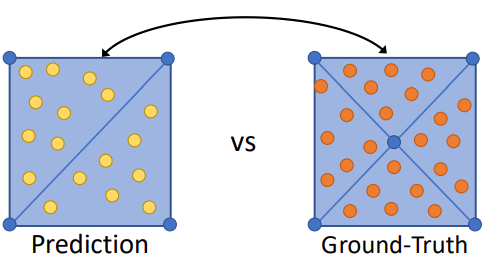
이제 Predict한 Mesh와 Ground Truth Mesh를 비교하는데에는 한가지 문제점이 발생한다. 같은 Shape에 대해 여러가지 표현 방법이 존재하기 때문이다.

이를 위해 다음과 같은 방법을 사용한다. ⅰ. Ground Truth Mesh에 Point를 Sampling하여 $\quad$ Point Cloud로 만든다. ⅱ. Predicted Mesh에 Point를 Sampling하여 $\quad$ Point Cloud로 만든다. ⅲ. Champer Distance를 사용해 두 Point Cloud간의 Loss를 계산한다.

하지만 이 방법에는 다음과 같은 문제가 존재한다.

• Train시에 Online으로 Sampling해야 하므로 이를 효율적으로 할 방법이 필요하다.
• Sampling을 통한 Backpropagation이 필요하다

---

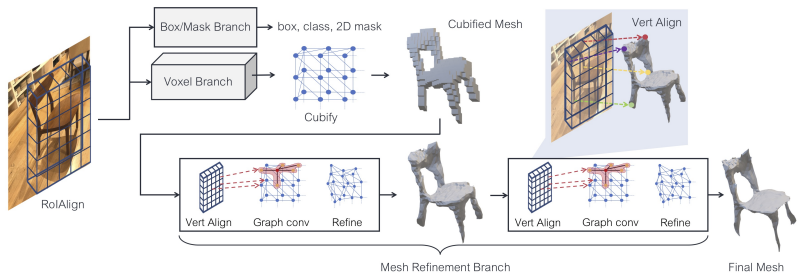
Paper2: Mesh R-CNN

Pipeline
	이전에 공부했던 Mask R-CNN은 BBox, Label, Segmentation Map을 찾아주었다. Mesh R-CNN은 여기에 Mesh Head를 추가하여 3D Mesh도 예측할 수 있도록 만든 모델이다. 이때, 특이한 점은 바로 Mesh를 예측하지 않고, Voxel을 예측한 후 이를 바탕으로 Mesh를 Predict하도록 설계한 점이다.

---

5. Implicit Representation

위에서 살펴보았던 모든 방식은 3D Shape를 Point들로 예측하는 방식, 즉, Explicit Representation이었다.
이 방식은 Memory도 많이 사용할 뿐 아니라 Discrete하다는 단점이 있다.

여기서는 3D Shape를 함수로 표현하는 방식인 Implicit Representation을 알아볼 예정이다.
함수로 예측하기 위해서는 어떤 좌표값을 Input으로 넣었을 때 그 좌표에 Object의 Inside인지 Outside인지에 대한 확률을 Output으로 출력하면 된다.

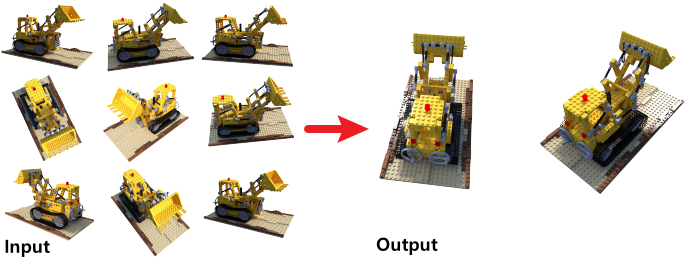
1) Nerf

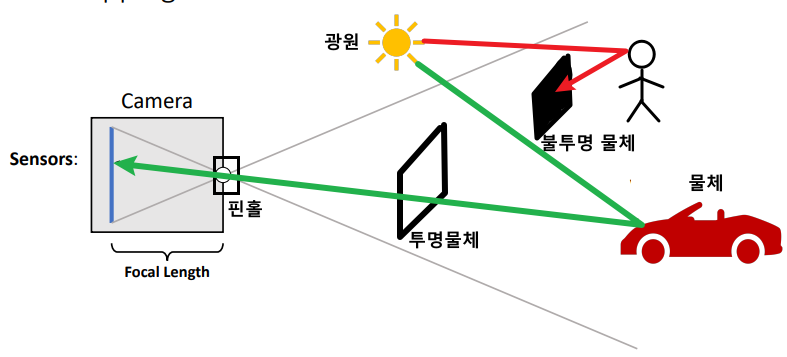
Nerf는 Camera Parameter를 알고 있을 때, 같은 장면에 대한 여러 이미지를 통해 새로운 각도에서의 ViewPoint를 찾아내는 문제를 다루고 있다.

Pinhole Camera Model	Radiance Field
Pinhole을 통해 물체를 인식하는 모델 카메라의 기본적인 원리를 나타내고 있고, 물체가 기록되는 과정을 알 수 있다.	우리가 추출할 수 있는 정보는 다음과 같다. $\quad$ⅰ) 색깔(Emit) $\quad$ⅱ) 불투명도(Opaque, Occlusion) 이 정보들을 공간내의 모든 점들에 대해 추출한 결과를 Radiance Field라고 한다. ex) 빈공간 $\qquad \qquad \quad \;\;$ 물체 $\quad$ ▷ Emit($c$) = “no” $\qquad$ ▷ Emit($c$) = “Red” $\quad$ ▷ Opaque($\sigma$) = 0 $\qquad$▷ Opaque($\sigma$) = 1

---

Volume Rendering

위의 Radience Field를 하나의 함수로 모델링하는 것을 Volume Rendering이라고한다.

direction이 $r(t) = \mathbf{o} + t\mathbf{d}$라고 할 때 Volume과 Color는 다음과 같이 표현된다.

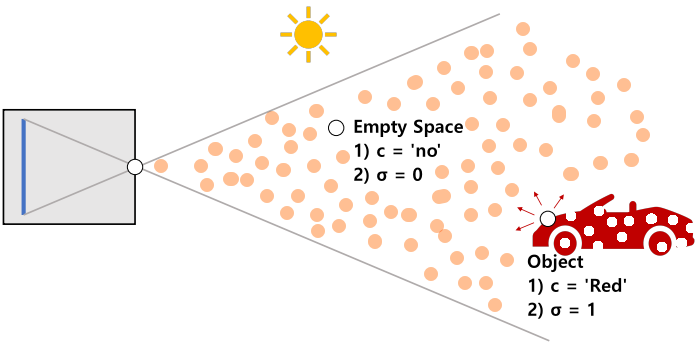
• Volume Density
  

  점 $p$에서의 밀도, 이 점이 얼마나 불투명한지 나타내는 값
  $\Rightarrow \sigma(\mathbf{P}) \in [0, 1]$

• Color
  

  점 p에서 방향 d로 방출되는 색상
  $\Rightarrow c(\mathbf{p}, \mathbf{d}) \in [0, 1]^3$

\[\Downarrow\]

Volume Rendering Equation

\[C(\mathbf{r}) = \int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t))c(\mathbf{r}(t), \mathbf{d}) dt \approx \sum \limits_{i=1}^N T_i(1 - e^{-\sigma_i \delta_i})\mathbf{c}_i \\ T(t) = e^{-\int_{t_n}^t \sigma(\mathbf{r}(s)) ds} \approx e^{-\sum \limits_{j=1}^{i-1} \sigma_j \delta_j}\]

• $T(t)$: Transmittance, 현재 Point에서 출발한 빛이 Camera에 얼마나 도달하는지
• $\sigma(\mathbf{r}(t))$: Opacity, 현재 Point의 불투명도
• $c(\mathbf{r}(t), \mathbf{d})$: Color, 현재 Point에서 Camera에 무슨색의 빛을 방출하는지

우리는 이 식을 Sampling을 위해 Approximate하여 사용한다.

이제 Sensor의 r방향에서의 Pixel값 $C(\mathbf{r})$에 대한 모델링을 하였으니 이를 활용하여 Deep Neural Network를 학습하면 된다.
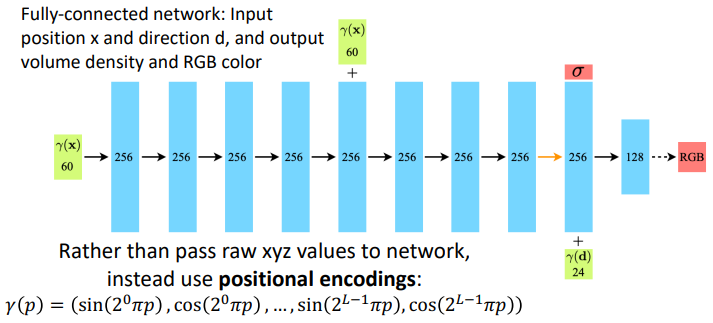
(Input= $p,d \quad \Rightarrow \quad$ Output $\sigma(\mathbf{r}), c(\mathbf{p}, \mathbf{d})$)

---

Architecture